Innanzitutto un bravo a Fabrizio e a Francesco per le loro esposizioni molto brillanti, che trovate nei commenti del quiz. Ricordiamo, poi, che questa è praticamente la risposta al quiz sulla formica, ma è anche un articolo tutto da leggere, soprattutto per le sue implicazioni finali e per l'utilizzo della serie armonica. Un paradosso che viene ancora una volta risolto, anche se necessita di tempo, tanto tempo...

Affrontiamo il problema in tre modi: uno grafico, uno discreto matematico e uno rigoroso analitico. Il primo ci lascia abbastanza incerti se consideriamo un elastico estremamente veloce nel suo stiramento; il secondo ci garantisce la giusta risposta; il terzo ci quantifica l'intera faccenda e ci fa sconfinare nella cosmologia.

Per cominciare affrontiamo il problema in modo grafico, lavorando direttamente sull'elastico e sulla formica secondo dopo secondo, mettendo in grafico il risultato.

Prendiamo delle velocità abbastanza comparabili... ad esempio:

u = velocità della formica  = 1 cm/s

v = velocità di stiramento dell'elastico = 3 cm/s

Fissiamo anche la lunghezza dell'elastico a riposo

d = 3 cm

In parole povere, secondo dopo secondo l'elastico si allunga di 3 cm, ossia passa da 3 a 6 a 9 a 12 a 15 cm e via di seguito. Secondo dopo secondo la formica percorre, invece, 1 cm, ossia passa da 0 a 1 a 2 a 3 cm, ecc.

La prima impressione è che la formica vedrebbe davanti a sé uno spazio da percorrere sempre crescente e, probabilmente, desisterebbe dall'impresa. Tuttavia, le formiche hanno la testa "dura" e non mollano facilmente.

APPROCCIO  GRAFICO

Innanzitutto, la formica si rende conto che anche stando ferma l'allungamento dell'elastico la fa muovere comunque.

Immaginiamo che essa si trovi all'istante iniziale a una distanza di 1 cm dall'inizio dell'elastico (il punto O fisso), In quelle condizioni il capo libero dell'elastico è ancora a 3 cm dall'inizio. Il rapporto tra il percorso fatto dalla formica e la lunghezza dell'elastico, ossia il suo punto di arrivo, è, quindi uguale a 1/3.

Tiriamo l'elastico di 3 cm, ossia portiamolo a una distanza c + v = 3 + 3 . La formica, pur essendo ferma viene trascinata dallo stiramento dell'elastico e viene a trovarsi a una distanza maggiore dal punto di partenza. Se prima era a 1 cm dal punto d'inizio, dopo lo stiramento si trova a (1/3) 6 = 2 cm. Il risultato è ovvio, qualsiasi punto dell'elastico è costretto a seguire il suo allungamento in base alla posizione che occupa. La formica era a 1 cm., ossia a 1/3 dell'elastico, e quindi deve mantenere questo rapporto che rimane costante. Il secondo dopo, l'elastico si porta a 9 cm e la formica viene trascinata a (1/3) 9 = 3 cm. Quello seguente la porta a (1/3) 12 = 4 cm, ecc., ecc.

In questo modo la formica fa qualche progresso verso il suo traguardo? Assolutamente no... Lei all'inizio distava 3 - 1 = 2 cm dal punto di arrivo, dopo un secondo a 6 - 2 = 4 cm, dopo due secondi si trova a 9 - 3 = 6 cm e poi a 12 -4 = 8 cm, ecc. D'altra parte nessun punto dell'elastico può mai raggiungere una sua estremità! Per maggiore chiarezza vediamo, in Fig. 1, ciò che abbiamo fatto finora e l'ovvio risultato...

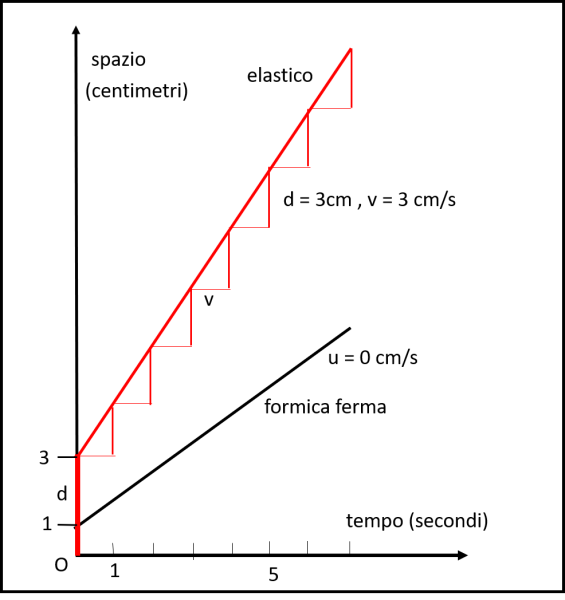
Tuttavia, la formica non sta ferma e oltre a essere tirata lontano dalla linea di partenza dallo stiramento dell'elastico, lei percorre 1 cm di sua volontà. Analizziamo questa situazione in modo "discreto", ossia invece di pensare a un moto continuo di elastico e formica, facciamoli muovere a scatti. Per metterci dalla parte del giaguaro, ossia nelle condizioni peggiori, tiriamo prima l'elastico e poi muoviamo la formica. Spieghiamoci meglio... Al tempo t = 0 tiriamo istantaneamente l'elastico di 3 cm, in modo che diventi 6 cm. La formica essendo nel punto di partenza non può essere trascinata e resta ferma.  Poi diamo il via alla formica che, nel giro di un secondo percorre 1 cm. Al tempo t = 1, avremo la formica  a 1 cm dal punto d'inizio, mentre la lunghezza dell'elastico è già di 6 cm. Tiriamo nuovamente l'elastico portandolo a 9 cm. Questa volta la formica viene trascinata di 1/6 della lunghezza dell'elastico (lei si trovava a 1 e l'elastico era 6).  Questo rapporto deve essere mantenuto  nel trascinamento e quindi la formica al suo centimetro guadagnato con le proprie forze viene aggiunto un tratto dovuto allo stiramento dell'elastico. In numeri, la formica si è mossa rispetto al punto fisso di (1/6) 9 = 1.5  per effetto dello stiramento e del suo percorso. Eseguito lo stiramento, la formica si muove nuovamente di 1 cm, portandosi a 2.5 cm dall'inizio. E' ora pronta al nuovo stiramento. Tuttavia, la sua posizione relativa all'elastico di 9 cm è adesso di 2.5. Lo stiramento fino a 12, perciò, le fa raggiungere la nuova posizione di  (2.5/9) 12 = 3.3 cm. E poi si può andare avanti sempre nello stesso modo fino a quando si vuole. Nella Fig. 2 abbiamo riportato le varie posizioni della formica (linea nera) e dell'elastico (linea rossa).

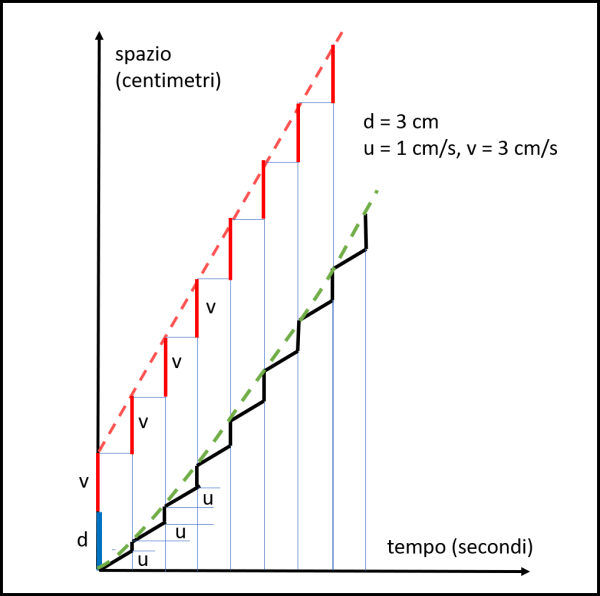
Quello che è importante notare in questa costruzione è che, a causa del  movimento proprio anche se decisamente piccolo, la formica è soggetta a un trascinamento, per effetto dello stiramento dell'elastico, che non rimane in rapporto costante con la lunghezza dell'elastico, come invece succedeva a formica ferma.

Il diagramma è fatto a "salti" di un secondo, ma è facile capire che tipo di curva descrive la posizione della formica.

Questo approccio "pratico" e manuale può darci qualche indicazione in più per poter rispondere alla domanda del "quiz" (chiamiamolo così...)? Purtroppo no, anche se lascia aperto qualche dubbio sul proseguimento della situazione. Tuttavia, pensiamo che avremmo potuto prendere la velocità del'elastico pari a 1 km/s e lasciare quella della formica pari a 1 cm/s. La nostra figura sarebbe diventata di dimensioni colossali...

No, graficamente non possiamo ottenere di più. Tuttavia, possiamo mantenere l'approccio a "scatti" e ragionare facendoci aiutare da semplici formule matematiche...

APPROCCIO MATEMATICO DISCRETO

Riprendiamo i valori generici delle due velocità e della lunghezza dell'elastico e lavoriamo con loro. Dedichiamoci al rapporto tra la distanza percorsa dalla formica e la lunghezza crescente dell'elastico. Ricordiamo ancora che questo rapporto resterebbe sempre uguale nel caso che la formica non si muovesse. Ma nel nostro caso, anche se di poco, si muove... Chiamiamo R(t) il rapporto tra il percorso eseguito dalla formica e la lunghezza dell'elastico.

Al momento t = 0 tiriamo l'elastico di lunghezza d di una quantità pari a v (come precedentemente, ciò che dovrebbe fare in un secondo lo eseguiamo in un tempo infinitesimo). Ovviamente la formica è ancora ferma nel suo punto di partenza uguale a 0, per cui

R(0) = 0

finito lo stiramento istantaneo, la formica si mette in moto e percorre, in un secondo) uno spazio pari a u. Avremo perciò

R(1) = u/(d+v)

Trascorso il primo secondo tiriamo istantaneamente l'elastico di un'altra quantità v. La formica resta ferma, ma viene trascinata dallo stiramento. Il rapporto R non cambia. Tuttavia la formica inizia a percorre un altro tratto pari ad u, ma il rapporto del suo nuovo tratto di  percorso rispetto alla lunghezza dell'elastico è adesso u/(d+ 2v). Questo rapporto, decisamente più piccolo di quello precedente, va sommato a lui, per cui abbiamo:

R(2) = u/(d+v) + u/(d + 2v)

In altre parole, la formica avanza sempre e soltanto di u ogni secondo, ma il suo percorso è sempre riportato in termini della lunghezza totale dell'elastico, la quale varia di secondo in secondo. Nella Fig. 2, i trattini della formica rettilinei (dovuti allo stiramento) non vengono considerati in quanto il rapporto resta invariato, ma il suo tragitto effettivo (tratto diagonale in funzione del tempo) deve sempre essere considerato relativo alla lunghezza dell'elastico che è aumentata di v.

Continuando in tal modo abbiamo la somma:

R(n) = u/(d+v) + u/(d + 2v) + u/(d + 3v) + .... + u/(d + nv)

Sembrerebbe che si sia ottenuto ben poco o, al più, che il rapporto aumenti ma di una quantità sempre più piccola. Le speranze della formica sembrano sciogliersi... Ma, studiamo meglio la nostra sommatoria.

Il termine  generico u/(d + kv) può essere sostituito da un termine ancora più piccolo. In questo modo saremmo ancora più sicuri del risultato finale, ossia se dovesse portare al raggiungimento del punto finale la somma di termini più piccoli di quelli reali, saremmo più che certi che lo farebbero anche i termini reali. Scriviamo, allora:

u/(kd + kv) ≥ u/(d + kv)

Il nuovo termine è sicuramente più grande di quello reale e quindi possiamo scrivere senza tema che la nuova somma R' deve essere minore di quella originale R:

R(n) ≥ R'(n) = u/(d+v) + u/(2d + 2v) + u/(3d + 3v) + .... + u/(nd + nv)

Se la somma dovesse raggiungere o superare il valore di 1, vorrebbe dire che la formica arriverebbe SICURAMENTE alla fine dell'elastico.

Il termine generico può ora essere scritto come:

u/(kd + kv) = (u/k)(1/(d + v)) = (1/k)(u/(d + v))

La parte u/(v + d) è sempre la stessa non dipendendo da k, per cui la sommatoria può scriversi:

R'(n) = (u/(d + v)) (1 + 1/2 + 1/3 + ... 1/n)

A questo punto basterebbe che la sommatoria dei numeri frazionari fosse maggiore o uguale a (d+v)/u per ottenere una R' ≥ 1 e, a maggior ragione, R ≥ 1.

Anche se sembra strano la sommatoria degli inversi dei numeri naturali (positivi) è una serie DIVERGENTE e prende il nome di SERIE ARMONICA. In altre parole esiste sempre un numero n tale che la somma sia maggiore di un numero N grande a piacere.

Si fa anche in fretta a dimostrare...

Come fatto precedentemente, cambiamo la nostra serie in una serie di valore minore:

Al posto di

1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + ....

scriviamo per ogni numero che non sia una potenza di 2 la potenza di 2 immediatamente successiva, ossia:

1 + 1/2 + 1/4 + 1/4 + 1/8 + 1/8 + 1/8 + 1/8 + ....

Questa seconda serie dà un risultato decisamente minore, ma tanto basta... infatti:

1 + 1/2 + 2(1/4) + 4(1/8) + ... = 1 + 1/2 + 1/2 + 1/2 + ...

E' sufficiente molta pazienza e perseveranza e alla fine si ottiene qualsiasi numero N grande a piacere.

Tornando a noi, ne segue che:

R(n) ≥ R'(n) ≥ 1

La formica, dalla vita infinita e dalla volontà di ferro riesce SEMPRE a raggiungere la fine dell'elastico. E questo vale per qualsiasi u e v, anche se enormemente diversi tra loro, e qualsiasi d.

Ad esempio potremmo prendere u =  1 cm/s e v = 1 km/s, con d = 1 km. Anche in questo caso, ovviamente, la formica raggiunge lo scopo. L'unico problema è il tempo di cui ha bisogno, ma lei non ha fretta!

Con l'approccio usato abbiamo dato la risposta alla nostra domanda e l'abbiamo dimostrata : NON ESISTE UN RAPPORTO LIMITE DATO CHE LA FORMICA VINCE SEMPRE. Tuttavia, non possiamo calcolare il tempo necessario. Per far questo dobbiamo usare un metodo analitico...

APPROCCIO ANALITICO

Lasciamo stare i salti temporali e entriamo nella problematica da un punto di vista più "fisico".

Abbiamo di fronte il moto del capo libero dell'elastico e il moto della formica che è in parte dovuto al trascinamento dell'elastico (a formica ferma) e in parte alla sua velocità u.

Utilizziamo un diagramma spazio-tempo per meglio capire la situazione (Fig. 3).

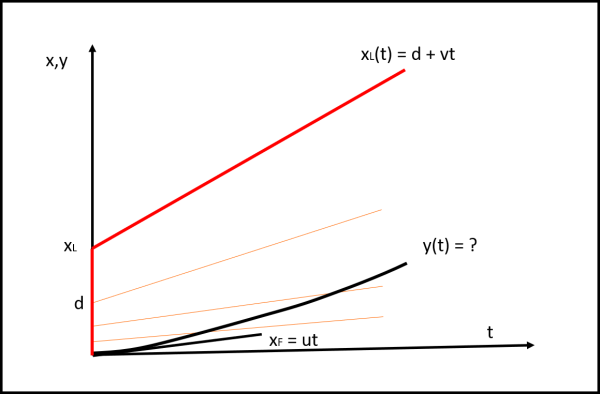
Qual è il moto del punto x_L (fine dell'elastico) in questo diagramma? Beh è un moto rettilineo uniforme del tipo:

x_L = d + v t

Ogni altro punto dell'elastico si muove insieme a lui in modo dipendente dalla sua posizione sull'elastico. In pratica, la velocità di qualsiasi altro punto x_i deve ridursi in base alla sua posizione, ossia:

v_xi = v_xi/x_L  = v_xi/(d + vt)

Ricordiamo che x_i/x_L rimane sempre costante, dato che si mantiene la proporzione tra posizione di qualsiasi punto fermo dell'elastico e quella del punto finale

In pratica, anche loro si muovono di moto rettilineo uniforme, ma con velocità sempre più ridotta a mano a mano che si va verso il punto O. Il punto O ha coordinata x = 0 e quindi non si muove. Tuttavia, la formica, che  è proprio nel punto O al tempo t = 0,  ha una sua velocità u che può farla spostare da quel punto critico. Ne segue che il suo moto sarà dato dalla combinazione di un moto rettilineo uniforme dovuto alla sua velocità propria u e a uno nuovamente rettilineo uniforme dovuto al trascinamento dell'elastico. Tuttavia, abbiamo un problema... questo secondo moto cambia continuamente, dato che cambia continuamente il rapporto x_i/x_L (non è più un rapporto costante come per un punto fermo!).

Siamo obbligati a introdurre una piccola equazione differenziale... in quanto conosciamo la variazione del punto-formica rispetto al tempo, ma non conosciamo il suo moto in funzione del tempo

Mi spiego meglio... noi conosciamo quanto vale la velocità della formica e possiamo scrivere senza problemi:

v_F(t) = u + v x_F(t)/(d + vt)        .... (1)

Ma, da questa relazione vogliamo ricavare il moto di x_F rispetto al tempo...

Per  maggiore chiarezza (spero) chiamiamo x_F con y, visto che è proprio la coordinata di cui vogliamo conoscere il moto rispetto al tempo (quello che prima era l'asse x diventa adesso  l'asse y, ma poco importa dato che noi cerchiamo la relazione tra y e il tempo)

Scriviamo nuovamente la (1), ricordando che se y(t) è la posizione della formica, la sua velocità sarà data dalla sua derivata y'(t):

y'(t) = u + v y(t)/(d + vt)      .... (2)

Questa è una "semplice" equazione differenziale del primo ordine (compare solo la derivata prima della funzione da determinare oltre che la stessa funzione). Per risolverla, sappiamo bene che dobbiamo fare l'inverso della derivata, ossia integrarla...

Ho detto "semplice", ma non lo è poi troppo. Possiamo, però, trasformare leggermente il problema (senza perdere in rigore analitico) e semplificare l'equazione differenziale (2).

Invece di considerare la posizione "assoluta" della formica, consideriamo soltanto la sua posizione rispetto all'elastico. In altre parole, consideriamo una nuova coordinata z che valga o all'inizio dell'elastico e che valga 1 alla fine di esso. Questa nuova coordinata rimane FISSA per ogni punto dell'elastico. Se esso si allunga, il suo punto finale vale sempre 1 e di conseguenza non varia nemmeno la coordinata z di qualsiasi altro punto.

Cosa vuol dire questo passaggio? Una cosa semplicissima... la coordinata x_L si deve trasformare in z_L = 1. Basta, perciò dividere x_L per (d + vt)  e abbiamo:

z_L = x_L/(d + vt) = (d + vt)/(d + vt) = 1

Analogamente tutti i punti x_i si trasformano adesso in z_i = x_i/x_L = x_i/(d + vt).

La formica deve fare lo stesso, ma lei non è ferma, dato che si muove comunque con velocità u (sarò ultra banale, ma i più esperti me lo permetteranno).

Essa si sposta da x₁ a x₂ ossia da z₁ = x₁/(d + vt) a z₂ = x₂/(d + vt) .

z₂ - z₁ = (x₂ - x₁)/(d + vt)

Basta ora dividere per il t₂ - t₁ e otteniamo:

(z₂ - z₁)/(t₂ - t₁) = (x₂ - x₁)/((t₂ - t₁)(d + vt))

Permettetemi di rendere infinitesima la differenza tra le coordinate e quindi anche quella dei tempi, e possiamo scrivere:

dz/dt = dx/(dt (d + vt))

Ma dz/dt = z'(t), mentre dx/dt = u... da cui:

z'(t) = u/(d + vt)         .... (3)

Abbiamo una nuova equazione differenziale, ma decisamente più semplice! Non ci resta che eseguire l'integrale della (3) per trovare la funzione z(t) che ha per derivata proprio u/(d + vt). Notiamo bene che la funzione z(t) che troveremo raggiunge il suo traguardo quando essa raggiunge z_L, ossia quando z = 1.

z(t) = ∫(u /(d + vt)) dt     .... (4)

Scusate adesso la monotonia della spiegazione, ma ne approfitto per richiamare gli integrali...

Innanzitutto, portiamo fuori dall'integrale ciò che è costante, ossia u. Nel contempo moltiplichiamo e dividiamo per v (all'interno dell'integrale). Otteniamo:

z(t) = ∫(u /(d + vt)) dt  = u ∫(v/(v(d + vt)) dt = (u/v)∫(v/(d + vt)) dt          .... (5)

Abbiamo portato fuori dall'integrale 1/v dato che anch'esso è una costante.

Ricordiamoci adesso la derivata del logaritmo in base e (ln)

d(ln t)/dt = 1/t

Analogamente sappiamo fare facilmente anche la derivata di ln(d + vt)

d(ln(d + vt))/dt = (1/(d + vt))d(d + vt)/dt = (1/(d + vt))(0 + v) = v/(d + vt)

Ma questa espressione è proprio quella che troviamo dentro l'ultimo integrale della (5).

Possiamo allora scrivere che :

∫(v/(d + vt)) dt = ∫(d(d + vt)/dt)dt

L'integrale non è altro che l'inverso della derivata, per cui se al suo interno abbiamo una derivata perfetta, l'integrale deve essere proprio la funzione di cui compare la derivata, ossia:

∫(v/(d + vt)) dt = ln(d + vt) + k     (dove k è la costante di integrazione)

O, in modo più completo:

z(t) = (u/v) ln(d + vt) + k         .... (6)

Per trovare k, basta ricordare che z(0 ) = 0, da cui:

0 = (u/v) ln d + k

k = - (u/v)ln d

La (6) diventa:

z(t) = (u/v) ln (d + vt) - (u/v) ln d = (u/v) (ln (d+ vt) - log d)

Ma sappiamo molto bene che la differenza di due logaritmi con la stessa base è uguale al logaritmo del rapporto, ossia:

z(t) = (u/v)ln((d+ vt)/d))         .... (7)

Questa è l'equazione del moto della formica lungo l'elastico. Essa raggiunge il punto finale quando z(t) diventa proprio 1 (ricordiamo che z_L = 1) e lo farà a un certo tempo T.

1 = (u/v)ln((d+ vT)/d)

ln((d + vT)/d) = v/u

e^{ln((d + vT)/d)} = e^v/u

(d + vT)/d = e^v/u

1 + vT/d = e^v/u

vT/d = e^v/u - 1

T = d (e^v/u - 1)/v                .... (8)

Questa espressione ha sempre una soluzione? La risposta è sì, dato che sia d che u e  v (maggiori di zero) sono numeri finiti e quindi anche T. Ciò che si trova è, però, che T può essere anche molto, molto lungo...

Utilizziamo, ad esempio, come proposto prima:

u =  1 cm/s

v = 1 km/s = 100 000 cm/s

d = 1 km

Non ci vuole molto a calcolare il tempo T in cui la formica raggiunge il suo traguardo: basta usare la (8)

T = 1 (e^{100 ooo} - 1)/1    secondi

T ≈ 2.8 · 10^{43 429}    secondi

Niente male! Basta avere tanta pazienza e sperare che l'Universo viva abbastanza... infatti, dalla sua nascita sono passati SOLO 4 · 10¹⁷ secondi!

ESTRAPOLAZIONE COSMOLOGICA: UNA FORMICA LUMINOSA

Noi stiamo vivendo in un Universo che si espande... e potremmo pensare ad un'analogia piuttosto interessante. L'universo stesso o -meglio- due galassie che si allontanano tra loro possono essere pensate come legate da un elastico in continua espansione. Ma c'è di più... questo elastico potrebbe "tirarsi" a una velocità anche superiore a quella della  luce: tutto gli è permesso.

Immaginiamo che la nostra formichina non sia altro che un fotone che parte da una delle due galassie (la possiamo immaginare ferma ed espandere l'elastico che è attaccato all'altra). A questo punto, senza pensare al tempo impiegabile, dovremmo concludere che il fotone-formica raggiungerà prima o poi l'altra galassia alla faccia della limitatezza della velocità della luce. Tuttavia, sappiamo molto bene che esiste una sfera, chiamata di Hubble, che stabilisce un limite alla luce che ci può raggiungere.

Le due cose appaiono in netto contrasto (e in realtà  lo sono), ma sappiamo anche che la costante di Hubble, che serve a stabilire il raggio della sfera di Hubble, è una costante solo spaziale e non temporale. Essa può continuare a variare sia in base al tasso di espansione sia in base al modello cosmologico scelto. Sappiamo, inoltre, che il raggio della sfera è proporzionale all'inverso della costante, ossia se lei decresce il raggio aumenta. Se il raggio aumenta, un fotone potrebbe benissimo trovarsi, durante la sua passeggiata da formichina, all'interno della sfera di Hubble e quindi riuscire veramente a raggiungere il suo traguardo. Nel passato ciò è successo realmente, dato che la luce di molti oggetti celesti ci ha raggiunto pur partendo da oggetti che erano ben oltre la sfera di Hubble relativa a quell'epoca.

Qualcuno potrebbe dire che la (2) implica una somma di velocità, di cui una sarebbe quella della luce. Eppure sappiamo che alla velocità della luce non si può sommare niente. Sì, ma nello spazio, non durante l'espansione di questo, che può portare a velocità ben maggiori senza colpo ferire. D'altra parte accettiamo il redshift cosmologico che praticamente ci dice che la lunghezza d'onda viene allungata dall'espansione,

Una visione cosmologica decisamente semplificata, che ha sollevato molte discussioni e scontri. Io, anche, la vedo un po' tirata per i capelli, ma valeva la pena accennarla.

Complimenti a chi è arrivato fino in fondo

QUI il quiz originario.