Questo articolo è stato inserito in due sezioni dell'archivio: velocità della luce e spaziotempo / cosmologia

 

In questo articolo cercherò di eliminare la confusione che si fa tra effetto doppler e redshift cosmologico (spesso una differenza non compresa da tanti divulgatori non professionisti). Provo, perciò, a spiegare in modo semplice (senza formule che ci porterebbero troppo in là) la profonda e fondamentale differenza concettuale. Essa va tenuta sempre in conto anche quando si applicano al redshift le formule dell’effetto doppler. Ciò si può anche fare, vista la somiglianza “pratica”, ma con estrema cautela: le cause e le grandezze fisiche coinvolte sono, infatti, completamente diverse. La stessa legge di Hubble va compresa e applicata con la dovuta attenzione. Tanto che ci sono, dico due parole anche sul redshift gravitazionale (un’altra cosa ancora). Per maggiori chiarimenti invito tutti ad andare a rileggere i molti articoli dedicati allo Spazio-Tempo e all’espansione dell’Universo (QUI).

In italiano si chiama spostamento verso il rosso (ma esiste anche uno spostamento verso il blu). In inglese vi è un termine a prima vista uguale: redshift. Purtroppo, dato che i due termini sembrano la stessa cosa, molto spesso i libri li trattano nello stesso modo. Mai errore è stato concettualmente più grande, anche se l’applicazione pratica può essere la stessa (fino a un certo limite).

In questo articolo, senza entrare nel campo dei calcoli relativistici più complessi, cerco di dimostrare, attraverso alcuni esempi, che anche se le due cose possono sembrare analoghe, e che un certo formulario si può usare per entrambe, le motivazioni fisiche che stanno alle loro spalle sono completamente diverse. Senza comprendere questa differenza si possono commettere errori sia pratici che concettuali enormi.

Posso già dirvi che la relatività ristretta, da sola, non riesce a diversificare l’applicazione pratica e che per descrivere il redshift, oltre certi limiti, è necessario costruire uno modello di base, che nel nostro caso è quello dell’Universo in espansione.

Cosa ci indica l’uguaglianza redshift = spostamento verso il rosso? Beh… un concetto che ormai conosciamo molto bene, soprattutto dopo gli articoli scritti sull’origine della spettroscopia. Uno spostamento di una generica onda luminosa (che potrebbe essere anche sonora) verso lunghezze d’onda maggiori. Il termine, perciò, definisce solo un effetto e non una causa.

Questo effetto è facilmente calcolabile: si conosce molto bene lo spettro luminoso costruito in laboratorio (e quindi in condizioni di quiete) e si misura lo spostamento che si osserva nella luce che proviene da un astro. Questo lo possiamo fare con facilità, dato che lo spettro emesso deve essere identico sia sulla Terra che in qualsiasi luogo dell’Universo. Una certa lunghezza d’onda è la stessa ovunque. Questo è il primo concetto, banale finché volete, che bisogna tenere bene a mente: qualsiasi oggetto celeste emette secondo un unico spettro luminoso, ossia a ogni lunghezza d’onda corrisponde una ben definita energia. Ne parleremo anche riguardo al modello atomico di Bohr e alla curva di corpo nero (QUI)…

Uno spostamento di una lunghezza d’onda verso il rosso (ma anche verso il blu) può essere descritto da un numero senza dimensioni, facilmente misurabile.

z  = (λ – λ₀)/λ₀

Attenzione ho solo detto “misurato”, dato che esso non è altro che un effetto.

E’ veramente un numero costruito con molta attenzione: λ è la lunghezza d’onda osservata, mentre λ₀ è la lunghezza d’onda misurata in laboratorio e che deve essere perfettamente uguale a quella emessa dalla stella in esame. La divisione per quest'ultimo valore crea un numero senza dimensioni e lo normalizza rispetto alla lunghezza d’onda di riferimento. Insomma ne fa un numero indipendente dalla lunghezza d’onda che si osserva.

Prima di proseguire, vediamo il significato fisico di un’operazione che “subiamo” e che è ancora senza una causa. Spostare la lunghezza d’onda da una parte o dall’altra dello spettro implica un cambiamento d’energia della luce. Il vero problema è capire la ragione fisica che causa questa variazione di energia che continuiamo a chiamare spostamento verso il rosso e/o redshift, dato che siamo ancora bloccati al solo effetto, legato a un significato fisico, ma senza una motivazione altrettanto fisica.

Scriviamo bene la domanda che dobbiamo farci: “Perché la luce (o se preferite i fotoni), pur essendo stata emessa con una determinata energia, sembra, a un osservatore, mostrare un energia del tutto diversa?” Ho usato il verbo “sembra” proprio perché stiamo assistendo a un effetto e non possiamo avere la sicurezza che vi sia una sola causa a produrlo. Anzi, non abbiamo  alcuna certezza che ciò che osserviamo sia reale o solo apparente. La luce, con i suoi miraggi, ci ha abituato a molti scherzi…. Pensate che lo stesso Hubble si è sempre ben guardato dall’associare le sue misure a una causa sicura…

E’ ora di affrontare il toro per le corna: “Cosa provoca lo spostamento verso il rosso o il blu dello spettro elettromagnetico, che sappiamo misurare così bene?”

Le ragioni sono due (in realtà tre, ma l’ultima per il momento la tralasciamo) e sono completamente diverse. Qui sta il punto chiave di tutta la questione.

Effetto doppler

E’ un fenomeno comunissimo che normalmente si osserva direttamente quando riguarda le onde sonore, ma viene utilizzato comunemente in astrofisica relativamente alle onde luminose. Esso indica la direzione dello spostamento di una sorgente che sta emettendo luce. Se lo spostamento va verso il rosso la sorgente si allontana. Se va verso il blu la sorgente si avvicina.

L’utilità è ovvia, soprattutto se si pensa ai sistemi stellari binari e agli esopianeti. Oggi si riescono a misurare variazioni della lunghezza d’onda di una certa riga spettrale (le righe si misurano meglio che il continuo, ovviamente…) tali da calcolare velocità di spostamento di pochi metri al secondo. Attenzione: ho parlato di velocità. Posso farlo perché ho già ammesso la causa. Ripeto: ho potuto parlare di velocità perché sto già dicendo che vi è uno spostamento di una sorgente luminosa, ossia ammetto che esista una variazione di distanza in funzione del tempo. Pensateci bene, mi raccomando!

Potrei usare le solite figure che mostrano un’onda circolare che si propaga da una sorgente in movimento e mostrare lo schiacciamento e/o il dilatamento dei tempi di arrivo al ricevitore. Preferisco, invece, utilizzare uno schema molto più istruttivo che conosciamo bene dopo quel poco di matematica che abbiamo fatto. L’abbiamo utilizzato nientemeno che nella QED. Siamo sicuri, quindi, che è più che corretto!

Consideriamo la Fig. 1.

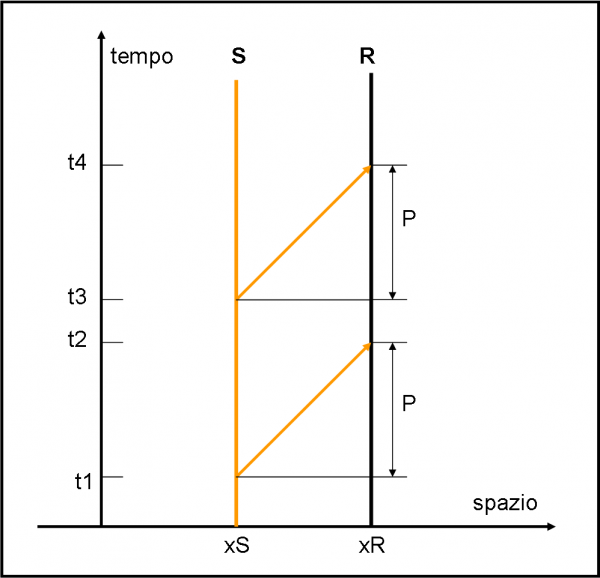
In ascissa mettiamo lo spazio percorso e in ordinata il tempo. E’ il modo migliore per “vedere”  le velocità e per legare tempi con lunghezze d’onda (che sono pur sempre delle lunghezze). Iniziamo col disegnare una sorgente S e un ricevitore R che non si muovono. Essi sono, quindi, rappresentati da due rette perpendicolari all’asse dello spazio (x). All’istante t1 facciamo partire da S un fotone o un’onda o come volete chiamarla. Esso si sposta sia nel tempo che nello spazio e se abbiamo scelto le unità di misura giuste il percorso compiuto è rappresentato da una retta a 45°. Fin qui niente di strano e niente di difficile.

All’istante t2 il fotone raggiunge il ricevitore R. Per semplicità, immaginiamo che sia arrivata una sola onda nel tempo t2 - t1. Ciò vuole anche dire che xR– xS è la lunghezza d’onda del fotone emesso. Cambiando lunghezza d’onda otterremmo che nello stesso intervallo di tempo arriverebbero più o meno di un’onda. Tutto lì. La velocità della luce deve essere sempre la stessa e quindi la retta deve sempre essere inclinata nello stesso modo. La differenza tra t2 e t1 non è altro che il periodo P, ossia il  tempo necessario a descrivere l’onda scelta. Vale la relazione ben conosciuta:

c = (xS – xR)/ t2 – t1) = λ/P

Se al tempo t3 la sorgente emette un altro fotone, esso giungerà in R al tempo t4 e continua a valere la stessa relazione di prima, ossia:

c = (xS – xR)/(t4 – t3) = λ/P

La sorgente e il ricevitore non si sono mosse e la lunghezza d’onda è rimasta sempre la stessa. In altre parole il nostro spostamento verso il rosso z è costretto a rimanere uguale a zero.

Cominciamo a complicare le cose in Fig. 2. Assumiamo che la sorgente S si allontani dal ricevitore con una certa velocità v. Questo fatto si traduce in un percorso della sorgente, inclinato rispetto alla perpendicolare all’asse dello spazio. In particolare, sta andando verso sinistra, ossia aumenta lo spazio tra S e R.

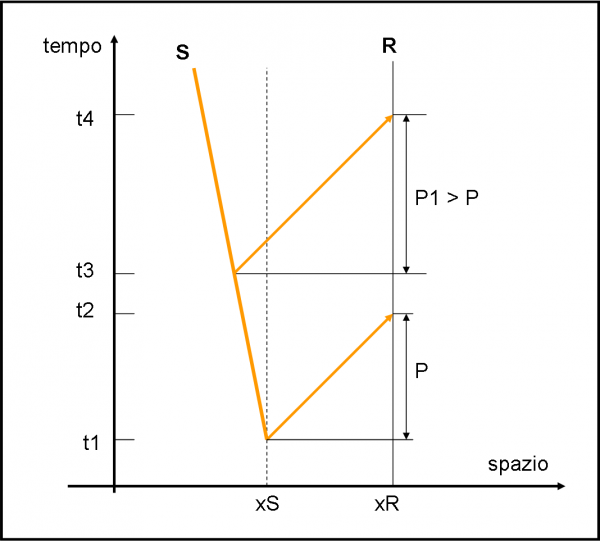
Vediamo cosa succede in modo grafico e molto immediato e intuitivo. Al tempo t1 la sorgente emette il suo fotone. Il fotone viaggia e non ha più alcun legame con la sua sorgente. Ormai sa dove andare! Al tempo t2 arriva nuovamente in R (che non si è mosso assolutamente). Otteniamo nuovamente la stessa identica relazione di prima:

c = λ/P

All’istante t3 la sorgente emette un nuovo fotone. Anch’esso si stacca e inizia il suo viaggio. La sua velocità è sempre la stessa (c) e quindi percorre spazi uguali in tempi uguali. Però, sta succedendo qualcosa… il tempo di arrivo t4 sembra non arrivare mai. Beh… basta fare la differenza tra t4 e t3. Accidenti, è vero! E’ maggiore di t2 – t1. Il che vorrebbe dire che è cambiato il periodo necessario a compiere un’onda. Siamo costretti a dire che ora abbiamo un nuovo P1 che, poiché la velocità della luce è sempre la stessa, mi porta a una nuova relazione:

c = λ1/P1

Cosa dobbiamo concludere? Che è cambiata la lunghezza d’onda del mio fotone! In realtà, però adesso sappiamo la causa, dato che abbiamo fatto muovere la sorgente.Possiamo concludere che lo spostamento della sorgente ha causato un allungamento apparente della lunghezza d’onda. Che bello! Ho ottenuto il mio spostamento verso il rosso e posso calcolare velocemente anche il numero z che vale:

z =  (λ₁ - λ)/λ 

Attenzione, adesso! Dato che ho introdotto una velocità di spostamento di S rispetto a R conosco anche la velocità v con la quale la sorgente si sposta dalla posizione iniziale (descrivendo la retta inclinata). Attraverso facili, ma noiosi, passaggi matematici legati alla figura (triangoli e cose del genere). si riesce a dimostrare facilmente che:

z = v/c        …. (1)

Cosa abbiamo imparato da queste figure e relazioni? Che lo spostamento verso il rosso non è un  effettivo cambiamento dell’energia del fotone, ossia della sua lunghezza d’onda. Lui viene sempre emesso nello stesso modo. Ciò che cambia è il tempo di arrivo al ricevitore e questo fatto fa apparire la lunghezza d’onda osservata maggiore di quella reale. Un fenomeno apparente, ma di utilità enorme per lo studio dei movimenti degli astri rispetto a noi..

La semplicissima relazione (1) ci permette di calcolare, conosciuto z (misurabile) la velocità v di spostamento della sorgente, assumendo fissa la Terra (cosa fattibile nel caso di doppie strette o di esopianeti).

Ribadisco ancora: la trattazione è perfetta e applicabile a tutto ciò che mostra un evidente movimento di allontanamento (o di avvicinamento).

Beh… una scoperta eccezionale che possiamo estendere ai movimenti di tutti gli oggetti nel Cosmo. Magnifico!

Nemmeno per sogno, cari amici…

La relazione che abbiamo trovato riguarda, ovviamente, movimenti di corpi celesti e quindi deve accettare la teoria della relatività ristretta di Einstein… In poche parole, la velocità v non può superare la velocità c. Purtroppo, la relazione (1) non si cura assolutamente di questo fatto. Lei è stata trovata attraverso la geometria euclidea. Per lei z può benissimo valere 1, quando v =c, ma anche molto di più...

E, infatti,  z, misurato per galassie non molto vicine, supera di molto il valore 1. Cosa vorrebbe dire? Che si può tranquillamente superare la velocità della luce? No, non diciamolo nemmeno per scherzo se no Einstein si rigirerebbe nella tomba. Possiamo solo concludere che la relazione (1), tanto bella e simpatica, può applicarsi solo quando la velocità v è molto minore di c.

Praticamente, funziona ancora per v uguale a circa 1/3 di c. Funziona per scopi pratici, ma concettualmente è già sbagliata. Essa darebbe luogo alla Fig. 3, dove riportiamo v/c in funzione di z.

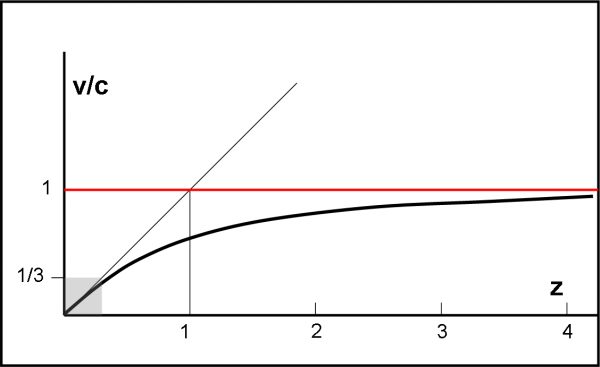
Come si vede molto bene, è una retta che passa per l’origine e che al crescere di z porta a valori maggiori di c. No, non possiamo permetterlo e allora è necessario tener conto della relatività ristretta che ci impone che la retta v/c = 1 non possa mai essere superata. La relazione, fatti i dovuti calcoli, cambia completamente e diventa:

z =  ((1+v/c)/(1-v/c))^1/2 - 1

Possiamo applicare questa nuova formula alla determinazione delle velocità di galassie lontane? Sicuramente sì, ma stiamo attenti che stiamo comunque ammettendo che vi sia un effettivo spostamento di una sorgente rispetto al ricevitore! Solo così ha senso parlare di velocità v. Non perdete mai di vista questo punto chiave, mi raccomando!

Per il momento, però, stiamo accettando che z sia dovuto solo all’effetto doppler, relativistico che sia oppure no.  Ci può andare anche bene, restando nella relatività ristretta e tenendo conto che ancora nessun oggetto osservato nell’Universo ha mostrato una velocità di allontanamento uguale alla velocità della luce: d’altra parte sarebbe assurdo, dato che per accelerare qualcosa a un tale velocità bisognerebbe avere un’energia infinita. Insomma tutto sembra tornare perfettamente.

Tuttavia, ci stiamo rendendo conto di quello che stiamo facendo? Non abbiamo avuto assolutamente bisogno di assumere un Universo in espansione oppure no. La faccenda non è assolutamente stata presa in considerazione. Non solo, ma ci siamo limitati alla relatività ristretta. Se considerassimo la relatività generale capiremmo che la velocità della luce può essere tranquillamente superata, ma solo e soltanto da parte dello stesso spazio.

Niente da fare, dobbiamo accettare che vi sia un’altra ragione fisica capace di mostrare un redshift, che però non ha niente a che vedere con l’effetto doppler, relativistico oppure no.

Redshift cosmologico

Chiariamo subito un punto fondamentale. Finora abbiamo fatto fisica basata su ciò che possiamo verificare nel mondo che ci circonda. Non abbiamo avuto bisogno di modelli teorici, al limite solo della teoria della relatività che possiamo ormai considerare parte della nostra realtà, a tutti gli effetti. D’ora in poi, invece, dobbiamo introdurre un modello teorico e solo sulla base di esso possiamo parlare di spostamento verso il rosso. Anzi, proprio le misure dello spostamento, legato alla nuova causa che può crearlo, ci serve a verificare il modello. Il modello non è altro che un Universo in espansione!

Innanzitutto, perde completamente di significato la parola “velocità”. La useremo spesso e volentieri, ma con un significato del tutto diverso da quello precedente. Non è assolutamente più uno spostamento di qualcosa nello spazio, ma un qualcosa che viene compiuto dallo spazio stesso. Se perde di significato la parola velocità, perde anche di significato la variazione di distanza. L’unica cosa che continua ad avere senso VERO è la variazione del tempo. Cerco di spiegarmi molto meglio…

Cosa vuol dire che vi è un’espansione dello spazio? In poche parole, che nasce continuamente nuovo spazio tra una certa sorgente e il ricevitore. Tuttavia, sia la sorgente che il ricevitore NON si muovono assolutamente! Mi raccomando, mettiamocelo bene in testa se no la confusione sarà sempre enorme.  Questa volta, perciò, la cosa apparente non è più la lunghezza d’onda che riceviamo, ma il moto di allontanamento tra sorgente e ricevitore.

La misura effettuata sulle lunghezze d’onda è la stessa dell’effetto doppler (ossia il numero z), ma il legame tra le grandezze fisiche è concettualmente diverso!  In altre parole, l’effetto doppler e il redshift si manifestano nello stesso modo ma descrivono grandezze e concetti del tutto diversi.

Nel resdhift l’unica cosa che succede (come dettato dal modello che abbiamo deciso di seguire) è l’espansione dello spazio in funzione del tempo. La velocità di recessione, quindi, è una velocità molto particolare. Essa è la velocità alla quale un oggetto celeste sembra allontanarsi da noi per effetto dell’aumentare continuo di spazio tra lei e noi. Non per niente si ha solo redshift e non blueshift, ossia spostamento verso il blu.

Ripeto ancora: sebbene in apparenza l’effetto dell’espansione dello spazio sia analogo a quello di un moto reale di oggetti, la relazione che contiene questo tipo di redshift non contiene più una velocità effettiva dei corpi, ma solo una velocità apparente che va considerata per quello che è, senza mischiarla con quella che causa l’effetto doppler.

Il guaio è che le formule sono esattamente le stesse, ma ben diversa è la loro interpretazione. Per piccoli valori di z il redshift può essere tranquillamente interpretato come effetto doppler, dove, però, si capisca bene che la velocità di allontanamento tra sorgente e ricevitore è ora una velocità apparente che chiamiamo di recessione per riuscire a diversificarla. Solo in questo senso può nascere la legge di Hubble:

u = H₀D

ossia:

z =  (λ₁ - λ)/λ = u/c = H₀D /c

Attenzione: L’ho chiamata u e non v proprio per farvi pensare sempre alla loro differenza. Anche D, che viene considerata una distanza, come già detto, perde di un vero significato, anche se può collegarsi a distanze effettive al variare del tempo. Sarebbe molto meglio (come cerco di fare sempre io) parlare di tempo necessario a partire dalla sorgente e arrivare al ricevitore. Solo il tempo è veramente legato alla continua intrusione di nuovo spazio, ossia all’espansione.

Il legame tra velocità e distanza che tanto affascina e tanto serve in cosmologia va intesa per quello che è. La sua importanza è enorme perché a partire da z (misurabile) ci permette di calcolare il tempo impiegato dalla luce per giungere fino a noi. Possiamo anche definirla distanza, ma stando molto, molto attenti…

Facciamo un esempio terra-terra per vedere come, anche ragionando in termini di effetto doppler, il valore di z deve tener conto della relatività ristretta.  La legge di Hubble va applicata nel modo giusto, per lo scopo giusto e per valori di z giusti. Cerchiamo di applicarla a una distanza reale e vediamo cosa ne viene fuori….

Prendiamo una galassia che ha mostrato un redshift di 7, ad esempio. Utilizzando la formula abbiamo il seguente risultato:

D = 95 miliardi di anni luce!

Ma possiamo anche andare oltre. La radiazione cosmica di fondo (la prima cosa che riusciamo a vedere dell’Universo) ha redshift di circa 1300 e quindi porta una distanza di circa 10¹³ anni luce, ossia diecimila miliardi di anni luce!

Ma siamo matti? Sappiamo benissimo che l’Universo ha 13.7 miliardi di anni e che la luce ha potuto percorrere in questo tempo al massimo questa distanza. Tutto sembra andare al diavolo, altro che modello di espansione!

Purtroppo molti divulgatori, che non hanno tenuto conto di questa netta differenza tra distanza vera e distanza apparente, non solo riportano conclusioni errate, ma, spesso, decidono che è giunta l’ora di cambiare il modello dell’Universo.

D’altra parte sembrerebbero avere ragione: com’è possibile vedere un oggetto che non può essere più vecchio di tredici miliardi di anni a una distanza di 95 miliardi di anni luce? Se questa fosse una vera distanza la luce non avrebbe certo avuto il tempo di raggiungerci.

Ciò che bisogna fare, innanzitutto, è utilizzare la formula di z riferita alla relatività ristretta.  Può bastare? No di certo. Sarebbe come mettere la polvere sotto al tappeto. L’errore vero è trattare l’espansione dell’Universo come se fosse un effetto doppler, ossia sostituire a velocità reali di allontanamento delle velocità che sono invece apparenti e dovute all’espansione dello spazio e non a un vero movimento dei corpi celesti.

Bisogna mettersi bene in testa che è lo spazio che si… allunga o si allarga o come preferite voi.

Per capire meglio la situazione bisogna entrare nella relatività generale, che ammette velocità maggiori di quelle della luce, quando chi si “muove” (o, meglio, si allarga) è lo spazio stesso. Per lui non ci sono limiti. Tuttavia, ci possono bastare alcune considerazioni di massima: la velocità di recessione non obbedisce alla relatività ristretta e non è vincolata a nessun limite superiore. La velocità è apparente così come diventa apparente anche la distanza trattata in termini “normali”.

Ne risulta un fatto indiscutibile, che deve sempre essere tenuto in conto: il redshift cosmologico non ha niente a che vedere con l’effetto doppler, anche se si possono usare formule analoghe. L’importante è saperle interpretare.

Voglio cercare di rappresentare, in modo molto semplificato, questa differenza fondamentale tra redshift cosmologico e effetto doppler. In particolare, evidenziare la netta differenza tra variazione di distanza (e quindi velocità) vera e apparente.

Non stupitevi se considero una sfera con i suoi meridiani e paralleli. Anzi, ci basta tagliarne una fetta  lungo i paralleli e studiare cosa capita. Prendiamo la Fig. 4. Sullo stesso parallelo si trova l’oggetto A e l’oggetto B. Possiamo definire due distanze tra di loro (restiamo sempre attaccati alla meccanica classica): quella angolare e quella lineare lungo la circonferenza.

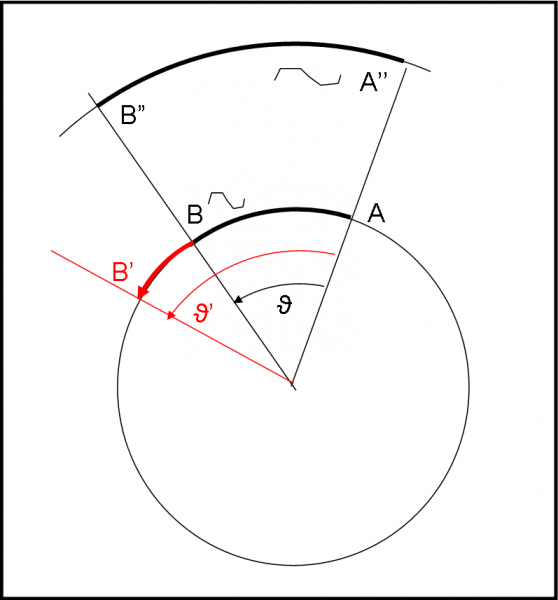
Abbiamo due modi per far variare la distanza di A rispetto a B. Il primo è far prendere una macchina o un aereo a B e farlo andare in B’, in verso opposto ad A, lungo il parallelo. Sicuramente cambia la distanza reciproca. Attenzione, però, cambia sia la distanza lineare sia quella angolare. Il tratto circolare tra A e B’ è maggiore di quello iniziale così come è anche maggiore l’angolo ϑ’ rispetto a ϑ  (in parole povere stiamo facendo variare la longitudine di un luogo…).

Perfetto. In questo caso abbiamo un effettivo spostamento di A rispetto a B e chi lo conferma chiaramente è la variazione dell’angolo. L'oggetto si muove veramente e assistiamo a un effetto doppler.

Eseguiamo, adesso, una nuova operazione che porta a una variazione “apparente” della distanza tra A e B. Quale? Aumentiamo il raggio della circonferenza, come se gonfiassimo la sfera di partenza (non stupitevi certo se il raggio può essere considerato il tempo). Cosa succede? A si porta in A’’ e B si porta in B’’.

Si sono veramente spostati? Nemmeno per sogno: nessuno ha preso un aereo o anche solo un’automobile. La loro apparente variazione di distanza è solo dovuta al gonfiamento della sfera (ossia allo scorrere del tempo). Chi o che cosa lo può dimostrare senza ombra di dubbio? L’angolo al centro. Esso è sempre rimasto uguale a ϑ. Non vi è stata nessuna vera variazione di distanza, nessuna velocità di spostamento di A rispetto a B, ma solo un allargamento dello spazio tra di loro.

Ogni cosa che stava percorrendo il tracciato da A a B si è trovata a dover compiere un tragitto lineare più lungo, ma in realtà ha sempre compiuto una distanza angolare che non è cambiata. Cosa capita al nostro povero fotone con la sua lunghezza d’onda mentre viaggia tra A e B? Una cosa molto semplice: subisce anche lui un allungamento della lunghezza d’onda: E’ un po’ come se l’onda si stirasse. E più la sfera si gonfia e più il fotone si allunga (mi raccomando, cercate di capire l’essenza e non pensate a un fotone spaghettizzato!). Questa volta la velocità è apparente, mentre è reale la variazione di lunghezza d’onda. Proprio il contrario dell’effetto doppler.

Come possiamo misurare di quanto si è gonfiata la sfera? Basta vedere quanto tempo ha impiegato il fotone a raggiungere A" partendo da B (o viceversa). In realtà, vorrebbe percorrere BA, ma, mentre lo fa. lo spazio si allarga e giunge in A solo quando esso si trova in A". Più tempo è stato in quel percorso, che continua ad allungarsi come un elastico, e maggiore è stato il suo allungamento.

Cosa riusciamo allora a “calcolare” misurando z, ossia l’effetto di allungamento? Essenzialmente, il tempo impiegato dal fotone a effettuare il percorso.

Ovviamente, però, questo fatto porta a dire che se il fotone fosse partito da C (più lontano di A rispetto a B) avrebbe impiegato più tempo e sarebbe perciò più “allungato”. Non è difficile legare strettamente il tragitto compiuto dalla luce lungo la circonferenza con l’allungamento dell’onda. Oltretutto, più l’oggetto era distante da A all’inizio e maggiore è stata la sua apparente velocità di allontanamento (quella detta di recessione). In poche e precise parole: a ogni punto è associata una differente velocità di recessione, malgrado la sfera si allarghi in modo unico. Al crescere del raggio (tempo), cresce la circonferenza su cui stanno, senza muoversi assolutamente, i vari punti.

Ecco perché si parla di strane "distanze" tra A e B e tra C e B. Sono distanze apparentemente cresciute senza nessun movimento vero tra i punti di partenza e di arrivo. Come si potrebbe mai parlare di distanza percorsa in un tempo t se la velocità di spostamento non esiste? A e B non si sono assolutamente spostate!

L’unica velocità che è presente nel nostro gioco di gonfiamento è sempre e soltanto la velocità della luce che resta sempre la stessa (la velocità del fotone). Così come l’unico vero modo di determinare le distanze tra i punti è definirle come tempo impiegato dal fotone, che può essere collegato facilmente con la variazione della lunghezza d’onda e quindi con z.

La distanza angolare non cambia e quindi non vi è alcuna velocità dei corpi coinvolti. Ciò che cambia è una distanza apparente che potremmo tranquillamente trascurare e considerare come vera distanza la distanza angolare. Questa distanza prende il nome di distanza comovente,  una costante rispetto all’espansione della sfera. Ovviamente, una distanza costante che causa distanze lineari apparenti sempre diverse a mano a mano che il tempo scorre e la sfera si gonfia, ma anche velocità di recessione diverse a seconda della distanza relativa tra i punti. E questo gonfiamento nel tempo che, questa volta, è indicato dal redshift z che si lega in qualche modo alla velocità di recessione.

In altre parole, molto più corretamente, questa variazione di distanza apparente possiamo intenderla come cambiamento di scala del nostro disegno.

Possiamo pure applicare la legge di Hubble per misurare delle distanze, ma dobbiamo sapere bene con che “distanze” abbiamo a  che fare.

vediamo le cose  in modo leggermente diverso e cerchiamo anche di rispondere a domande che spesso si fanno e che hanno, altrettanto spesso, risposte molto lacunose  e ambigue.

Una prima domanda è la seguente: “E’ possibile che nell’Universo ci sia qualcosa che SEMBRI, oggi, viaggiare a velocità maggiore della luce?” La risposta è abbastanza complicata e cercate di seguirmi molto bene.

Potrei rispondere: “Sicuramente sì”. Tuttavia, stiamo bene attenti: ciò non vuol dire che l’Universo ha un tasso di espansione maggiore di quello della velocità della luce, ma solo che vi sono punti talmente lontani linearmente da noi che la velocità apparente di recessione può anche essere maggiore di quella della luce.

Ma, accidenti, come possiamo osservare al telescopio oggetti che stanno andando più veloci della luce? Sembra una vera assurdità.  Semplicissimo, invece: perché quando la loro luce è partita la sfera era molto meno gonfia e quindi la luce è riuscita ad arrivare fino a noi, anche se in tempi molto lunghi. La stessa radiazione cosmica di fondo, che stiamo osservando oggi, non si espande ancora con una velocità apparente superiore a quella della luce. Ma questo accadeva 13,4 miliardi di anni fa, proprio il tempo impiegato per raggiungerci dalla luce che osserviamo ora! Non dobbiamo mai dimenticare che stiamo osservando il passato degli oggetti e che il presente potrebbe essere ben diverso.

Se riuscissimo a vedere, dall’esterno, l’Universo odierno, scopriremmo che attualmente il limite per cui la velocità di recessione è superiore a quella della luce si trova a una “distanza” che corrisponde a un redshift z di circa 1.5. Tutti gli oggetti oltre questo confine, attualmente, sembrano muoversi a velocità superiori a quelle della luce. Noi continuiamo a vedere la loro immagine del passato, semplicemente perché miliardi di anni fa, quando i fotoni hanno lasciato l’oggetto, la velocità di recessione rispetto a noi non era ancora superiore a quella della luce. Per chiarirsi ancora meglio le idee, basta riferirsi al cono di luce...

Questo significa che un giorno non vedremo più questi oggetti? Esattamente! Quando, con il trascorrere del tempo, arriveremo all’istante in cui dovremmo ricevere i fotoni emessi quando il moto apparente si è trasformato in superluminale, vedremo l’oggetto affievolirsi lentamente per poi scomparire.

Questo capiterà per oggetti singoli, come una galassia, la quale rimane sempre la stessa e quindi occupa una posizione fissa mentre il tempo scorre. Il rumore di fondo è invece un qualcosa che esiste dappertutto (e, soprattutto, che esisteva dappertutto) e quindi vi sarà ancora una qualche parte di esso che è partito quando la velocità di recessione rispetto a noi  era ancora sotto il valore della velocità della luce e che ci raggiungerà domani e dopodomani.

Qualcuno potrebbe chiedermi: “Ma allora la velocità di espansione cambia con il tempo?” No, no, assolutamente no! Cambia solo la velocità di recessione che è una velocità apparente ed è tanto più elevata quanto maggiore è la distanza (lineare e quindi anche lei apparente) tra gli oggetti considerati.

La sua variazione non implica un cambiamento nel tasso di espansione dell’Universo. Quest’ultimo è il valore dato dalla costante di Hubble. Oltretutto è un valore costante per il momento OGGI, dato che dipende dal momento in cui riceviamo la luce delle varie galassie partita in tempi molto diversi. Domani, magari, la costante cambierà, dato che cambierà effettivamente il tasso di espansione dell’Universo.

Come avete notato, non ho assolutamente parlato di velocità di espansione dell’Universo che è un concetto piuttosto pericoloso che può portare a gravi confusioni. Non confondiamo, comunque, tasso di espansione e velocità di recessione. Il primo è qualcosa di reale (secondo il modello usato) e valido per tutto l’Universo (calcolato usando galassie non eccessivamente distanti, dato che anche la legge di Hubble diventerebbe inutilizzabile). La seconda è un qualcosa di apparente e che dipende solo dal tempo di cammino dei fotoni e che ricavo da z.

In conclusione: la velocità di recessione e quella che causa l’effetto doppler non hanno nulla in comune, sono due grandezze completamente diverse. Per comodità e per spiegare le proprietà dello spostamento, la velocità di recessione è interpretata come redshift per effetto doppler. In questo modo la relazione che si ricava è semplice e permette di mettere in evidenza alcune importanti proprietà dell’Universo, come appunto la legge di Hubble. Tuttavia, ricordiamo che ciò si può fare perché le velocità di recessione sono minori di quella della luce.

Visto che abbiamo fatto trenta, facciamo anche trentuno…

Redshift gravitazionale

Secondo la teoria della relatività generale, anche i fotoni sentono la forza gravitazionale a causa della distorsione dello Spazio-Tempo dovuta alle masse. In parole (molto) semplici, la luce sente la forza di gravità. Poiché i fotoni non hanno massa a riposo ma hanno energia, la forza di gravità fa diminuire quest’ultima, spostando la lunghezza d’onda verso il rosso.

Questo fenomeno è chiamato redshift gravitazionale e non ha nulla a che vedere né con l’effetto doppler né con quello cosmologico, sebbene l’effetto prodotto sia ancora una volta lo stesso.

Il redshift gravitazionale coinvolge grandezze fisiche diverse, in particolare legate alla forza gravitazionale prodotta dal corpo celeste che “devia” e “allunga” la luce. Una formula approssimata è la seguente:

z = Δλ/λ = (λ - λ₀)/λ₀ ≈ GM/(c²r).

Mamma che fatica! Spero che serva…

 

NEWS!! - La legge di Hubble ha ufficialmente cambiato nome, d'ora in poi di chiamerà LEGGE di HUBBLE-LEMAITRE. Il motivo ve lo raccontiamo QUI