Categorie: Matematica
Tags: calcolo distanze geometria quiz
Scritto da: Vincenzo Zappalà
Commenti:15
Rifacciamo le autostrade a Corruptonia ***
Questo articolo-quiz ha un tono scherzoso, dato che era già pronto prima della tragedia. Non voglio cambiare niente e faccio poca fatica a pubblicarlo. In attesa che mi riprenda un po' e che smaltisca le odiose pratiche burocratiche, vi lascio un ricordo in attesa di tempi migliori che DEVONO venire sia per stare dietro a mia figlia, sia perché il tempo a mia disposizione non è tanto... I vostri calcoli e riflessioni a riguardo saranno un angolo di gioia in questo momento così nero. Grazie a tutti. Non so quando riuscirò a rispondere (dipende dai momenti), ma non abbiate timore a commentare e a risolvere... A presto!
Questo articolo, come facilmente comprensibile, è solo una "favola", dato che non possono esistere (?) Nazioni ridotte come l'immaginaria Corruptonia. Ma, la favola diventa ancora più irrealistica nel momento in cui si riesce a invertire il corso degli eventi e si cerca di trovare una soluzione onesta ed economica.
Nel Paese di Corruptonia, tutte le opere pubbliche sono state fatte con lo scopo di risparmiare e di intascare "mazzette". E quando si dice risparmiare s'intende usare materiale non idoneo e a rischio di crolli e di rapido deterioramento. Tuttavia, nessuno vedeva, sentiva e soprattutto parlava e si era arrivati a una situazione insostenibile, solo dopo una valanga di incidenti. In poche parole, tutte le strade che connettevano le città più importanti erano diventate intransitabili.
A questo punto comincia la parte più incredibile della storia: un nuovo governo decide di riparare ai misfatti e, pur cercando di risparmiare il più possibile, di affidare i lavori a imprese serie che rispettino tutte i vincoli di massima sicurezza. Finalmente nel cemento viene anche messo del vero cemento e non si lesina sul ferro. Insomma, un mondo veramente da favola per bambini...
I primi lavori devono interessare i nuclei più trafficati della Nazione, quelli che collegano le città più industriali e/o più visitate turisticamente. Ne sono stati scelti 4, in cui si trovano 3, 4, 5 e 6 città rispettivamente. Vediamo le 4 aree interessate in Fig. 1 (i nomi delle città sono stati omessi per questione di "privacy", per cui potete chiamarle come volete).
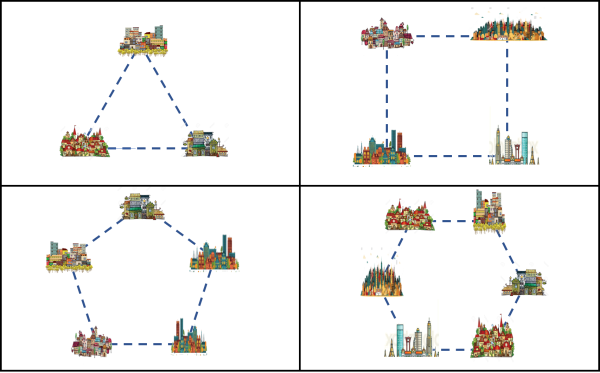
Caso vuole (o forse la configurazione risale a civiltà più antiche) che le posizioni delle città rispecchino perfettamente quelle dei vertici di poligoni regolari. In particolare, un triangolo equilatero, un quadrato, un pentagono e un esagono, come mostrato dalle tracce evidenziate in Fig. 1.
Viene bandita la gara per una nuova rete autostradale che colleghi tra loro TUTTE le città di ogni singola area. In altre parole, la rete autostradale deve raggiungere ogni città. Poco importa se per andare da una città ad un'altra si debba fare un percorso più lungo di quello, a prima vista, più conveniente. I mezzi di trasporto e le automobili vanno ad acqua e consumano pochissimo. Questo risultato è stato raggiunto velocemente dopo che sono stati imposti, come doveri sacrosanti, la diminuzione gli introiti delle aziende produttrici di energia e l'aumento dei vantaggi per la popolazione. Presa questa decisione è bastato dare via libera alla ricerca e... ecco il miracolo! Non per niente siamo in una favola...
Vi sono, però, alcuni vincoli tassativi:
1) Due città devono essere connesse da uno o più segmenti rettilinei autostradali.
2) I segmenti rettilinei non possono intersecarsi tra loro, Possono solo toccarsi nei punti terminali (meglio non costruire ponti o gallerie... non si sa mai).
3) Bisogna assolutamente risparmiare sul manto stradale. Ne segue che la lunghezza totale dei segmenti autostradali deve essere la minima possibile.
Provate anche voi a partecipare alla gara, prospettando le soluzioni migliori per le 4 aree interessate, calcolando anche la lunghezza totale delle autostrade in ogni singolo caso. Chissà che non riusciate ad avere l'appalto (ma senza mazzette)!
La soluzione la trovate QUI
15 commenti
Ciao Enzo, credo siano i raggi che collegano il baricentto della figure con gli spigoli. Grazie, Marco
P.S.: Non mollare, fatti sentire.
p.p.s. Finalmente, grazie a te ho, terminato il mio lavoro.
Provo a dire la mia, anche per far sentire che ci siamo.
Ho messo a confronto due possibilità. La prima è il collegamento a stella a partire la centro della circonferenza che iscrive il poligono. La seconda segue i lati del poligono. In quest'ultimo caso posso risparmiare uno dei lati poichè il collegamento fra le due città estreme è comunque garantito facendo il percorso nel senso opposto.
Nel grafico ci sono le lunghezze delle autostrade nei due casi per ciscuno dei 4 poligoni. Per i primi 2 conviene la configurazione a stella, per i secondi due quella che segue i lati.
Nella configurazione a stella la lunghezza totale delle autostrade cresce linearmente con il numero delle città, mentre nell'altra configurazione va verso un valore limite pari alla lunghezza della circonferenza che iscrive il poligono.
Il grafico
caro Fabry,
ti ringrazio per aver commentato... sapessi quanto mi aiuta in questi momenti. Il blog è troppo per me ed è una vera ancora di salvezza.
Torniamo a noi e via con il Circolo!
La faccenda è un po' più complicata, anche se in due casi la risposta è stata data... Vi lascio ancora a pensare, sapendo che siete diabolici!!!!
Ho esplorato la possibilità che le diramazioni non siano al centro del poligono.
Per il quadrato il risultato è stato positivo. Un percorso di questo tipo è migliore di quello a stella.
Il percorso minimo (3,86) si ottiene con un angolo di 30 gradi tra il lato orizzontale ed i percorsi obliqui.
Ho provato ad applicare questo tipo di percorso anche al pentagono e l'esagono, ma ho ottenuto lunghezze superiori a quelle della figura del mio commento precedente.
OK Fabry, ma quello che conta non è l'angolo di 30...
Aspetta... aspetta.... non mi torna la lunghezza totale...
Il procedimento che ho seguito l'ho riportato nella figura sotto.
Ho cercato di trovare quale dovrebbe essere la minima lunghezza dei percorsi quando parte del percorso per raggiungere due nodi è in comune. Mi sembra che il problema sia ottimizzare la posizione del punto di diramazione. Per individuarlo ho utilizzato come parametro l'angolo beta. L'angolo alpha dipende dal poligono.
Secondo questo ragionamento sembra essere proprio l'angolo beta che conta, indipendentemenet dall'angolo alpha.
Nel caso del quadrato, con alpha=90º e la struttura che si ripete due volte, la lunghezza totale è=R\sqrt{2}\left&space;(\sqrt{3}+1)&space;\right&space;)\simeq&space;3,86\,R)
Forse non ti torna il 3,86 perchè non ho detto che ho preso come riferimento il raggio R della circonferenza che circoscrive il poligono.
Usiamo come unità il lato del poligono...e per il quadrato sembra OK... prova con il pentagono...
Il caso del pentagono è più complesso, perchè non c'è una simmetria adatta. Si può applicare la doppia stella a 4 vertici e connettere direttamente al centro il 5°.
Più corta del collegamento lungo il perimetro che è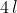
.
Probabilmente si può ottenere anche un risultato più corto decentrando i centri, ma è molto complicato trovare i tre punti ottimali. Ci sto provando.
Ho provato la configurazione a stella doppia anche con l'esagono.
Qui la struttura si ripete 3 volte e l'angolo alpha è di 60º. La lunghezza che ottengo è
Il migliore collegamento rimane quel del perimetro con un lato mancante che è lungo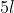
.
caro Fabry...
non sei lontano, ma c'è ancora un qualcosa che tieni poco in conto... i punti di snodo.
Puoi anche ragionare su un approccio più generale del triangolo e considerarlo sia acutangolo che ottusangolo. Questo approccio potrebbe aiutare a trovare una certa caratteristica degli snodi... Vi è un salto decisivo quando...
ancora grazie per continuare a provare!
Non mi sono ancora arreso. La soluzione trovata per il triangolo e quadrato non va bene per il pentagono che ha un numero dispari di vertici. Per il pentagono ci vuole qualcosa di diverso.
Ho provato ha posizionare in modo generico gli snodi rispettando comunque la simmetria del pentagono. Poi ho cercato di ottimizzare la loro posizione per trovare il percorso minimo che collega i vertici.
Il risultato è in questa figura.
La lunghezza è circa 3,89 l. Quello che sembra più interressante è che, anche in questo caso, i rami che escono dagli snodi formano 3 angoli di 120º come per il quadrato e triangolo. Che questa regolarità fosse presente nelle altre figure veniva dal fatto che si ripeteva più volte la stessa struttura. In questo caso le strutture utilizzate sono diverse, ma la regolarità sembra rimanere. Dico sembra perchè, avendo risolto il problema numericamente, rimane una piccola incertezza sul risultato.
Questa regolarità fa pensare che ci possa essere un legame tra snodi con rami a 120º e porcorsi ottimali. Legame che però non ho trovato.
Aggiungo qualcosa sul percorso fatto per trovare il posizionamento degli snodi.
Per la simmetrie del pentagono, uno degli snodi deve essere su un asse di simmetria, diciamo a distanza w dal centro. Gli altri 2 simmetrici rispetto all'asse che assumo come asse delle ascisse. Quindi, le coordinate generiche dei 3 snodi dovrebbero essere (w,0), (x,y) e (x,-y). Date queste coordinate è possibile trovare l'espressione della lunghezza del percorso come funzione di w,x,y, L(w,x,y). Ora occorre trovare la tripletta w,x,y che rende minima questa lunghezza. Fino a qui è possibile procedere manualmente, nei passaggi successivi sono dovuto ricorrere a strumenti informatici. Una possibilità è quella di risolvere numericamente il sistema di 3 equazioni che si ottengono derivando parzialmente L(w,x,y) rispetto a ciscune delle 3 variabili. Un'altra possibilità è quella di inserire la funzione in uno strumento informatico di ottimizzazione numerica che fornisce direttamente il risultato.
Dovo dire che sono positivamente sorpreso della ricchezza di strumenti informatici disponibili legalmente in rete. In questo caso direi il lato "oscuro" di Internet, in contrasto con le nefaste scie luminose lasciate dai satelliti.
caro Fabry,
non capisco il problema del commento... comunque l'ho sbloccato, ma non so proprio come mai sia successo. Prova a mandare un commento molto stringato e vediamo cosa succede..
Sugli angoli di 120 ° hai visto giusto!!! L'inizio della questione nasce con il punto di Fermat per il triangolo e poi Steiner ha trovato il suo percorso minimo utilizzando punti simili (il loro numero è parti al numero di lati meno due). La faccenda funziona, però, solo per angoli interni al poligono inferiori a 120°, dopo di che i punti di Steiner coincidono con i vertici e la minima distanza rimane la somma dei lati meno uno...
Come dicevo il problema non si riesce a generalizzare... comunque ne parliamo nell'articolo di risposta...
Comunque BRAVO!
Tra parentesi, hai trovato facilmente il modo di calcolare la lunghezza delle autostrade del pentagono? E' sempre un bell'esercizio di trigonometria...
Nel caso di posizionamento generico degli snodi, non sono riuscito a trovare trigonometricamente la lunghezza delle autostrade. Sono ricorso ad un metodo direi analitico su un riferimento con origine nel centro del pentagono e con asse delle ascisse l'asse di simmetria del pentagono. In questo riferimento, i vertici del pentagono hanno coordinate,R\,sin\left&space;(&space;i\,\frac{2&space;\pi}{5}\right&space;)\right)\;&space;\;&space;con\;i=0\cdots&space;4)
e ho dato le coordinate generiche (w,0), (x,y) e (x,-y) agli snodi. Dalle coordinate degli estremi ho trovato le lunghezze dei segmenti delle autostrade. Dalla loro somma ho ottenuto l'espressione della lunghezza totale come funzione di 3 variabili L(w,x,y). Ho quindi trovato la terna di variabili che rende minima questa funzione.
Sono riuscito a portare a termine il lavoro solo con l'aiuto di strumenti informatici perché l'espressione di L(w,x,y) è complessa e lo è ancora di più l'espressione delle sue derivate rispetto alle tre variabili.