Questo articolo risponde alla richiesta per la costruzione delle reti autostradali ottimali come richiesto QUI e QUI. Vediamo di fare i vari calcoli e di introdurre un nuovo tipo di percorso minimo.

Il nostro Fabrizio ha già fatto fin troppo, riuscendo a trovare le rete autostradali più corte nelle nostre 4 zone. In realtà, il percorso utilizzabile deriva da un problema giudicato, in gergo tecnico, NP-hard, ossia senza soluzioni polimoniali non deterministiche, che corrisponde a problemi  che siano almeno difficili come il più difficile dei problemi legati a polinomi non deterministici. In poche parole, una sua generalizzazione è ben al di là dello scopo del nostro Circolo. Tuttavia, almeno per un numero di punti piuttosto ristretto la soluzione esiste e prende il nome di Albero Euclideo di Steiner.

La definizione generale è la seguente:

Dati N punti nel piano, trovare una connessione tra essi attraverso segmenti rettilinei, con l'inclusione di punti di snodo supplementari, la cui lunghezza sia la più corta possibile.

In tal modo si evita qualsiasi intersezione tra i vari segmenti, mentre il numero di punti supplementari (punti di Steiner) è uguale al numero dei vertici meno due.

Nel caso più semplice, quello del triangolo, si parte esattamente dal punto di Fermat-Torricelli e la strategia operativa estende questo concetto a poligoni con un numero di lati maggiore. Notiamo che stiamo ragionando con poligoni, i cui angoli interni devono seguire regole ben note. Il problema diventa "terribile" quando i punti sono disposti in modo qualsiasi nel piano...

Ricordiamoci di quanto detto a proposito di Napoleone e del suo metodo per trovare il punto di Fermat solo attraverso delle circonferenze e definiamo di nuovo questo punto estremamente importante in molti problemi (non solo "militari" ...).

Il punto di Torricelli-Fermat

Dato un triangolo qualsiasi di vertici A, B e C, il punto di Torricelli-Fermat è quel punto che minimizza la somma delle distanze dai vertici.

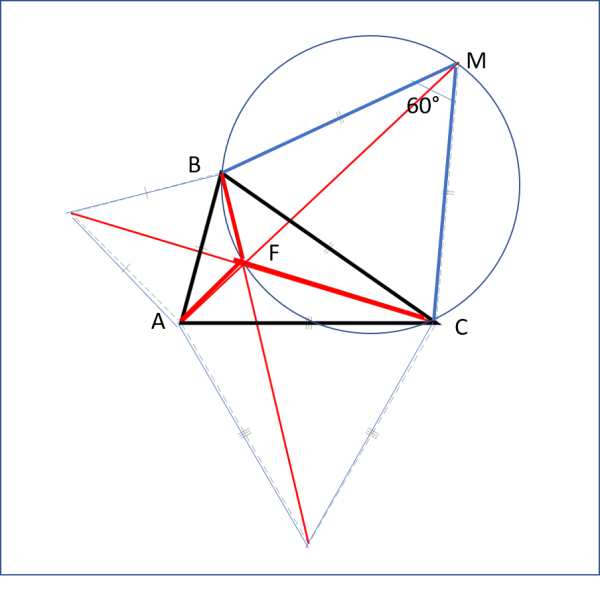
La scoperta deriva dalla soluzione data da Torricelli a un problema proposto da  Fermat. Il punto di Torricelli-Fermat è individuato dall'intersezione delle tre linee ottenute congiungendo ciascun vertice del triangolo con il vertice, non appartenente al triangolo, del triangolo equilatero costruito sul lato opposto a tale angolo, esternamente al triangolo. La Fig. 1 mostra un triangolo con il suo punto di Fermat.

Dato che il quadrilatero BFCM è iscrivibile in una circonferenza, ne segue che l'angolo in F deve essere di 120°. Analogo discorso vale per gli altri due lati e, di conseguenza, le congiungenti dei vertici del triangolo originario con questo punto formano angoli di 120° tra loro.

Quando, invece,  un triangolo ha un angolo maggiore di 120° il punto di Fermat è posto sul vertice dell'angolo ottuso.

Vediamo in modo estremamente semplice, in Fig. 2, come quest'ultima deduzione risulti ovvia variando un angolo di un triangolo di partenza qualsiasi.

Il triangolo di partenza sia A₁BC , Il suo punto di Fermat è F e tale rimane facendo scorrere A1 in A2, A3 e così via. Quando A1 coincide con F, l'angolo è esattamente uguale a 120°. Facendo scorrere A1 verso F1, F2, ecc. il punto di Fermat continua a spostarsi coincidendo con il vertice.

Ne segue che per triangoli acutangoli la minima distanza autostradale è quella che congiunge F con i tre vertici, mentre per triangoli con angolo maggiore di 120° il percorso minimo è quello che congiunge il relativo vertice con gli altri due.

Ovviamente, nel caso della prima zona interessata dalle nostre autostrade, il triangolo è equilatero e, quindi, il punto di Fermat (o di Steiner) è quello indicato in Fig. 3 e le autostrade da costruire sono i tratti rossi.

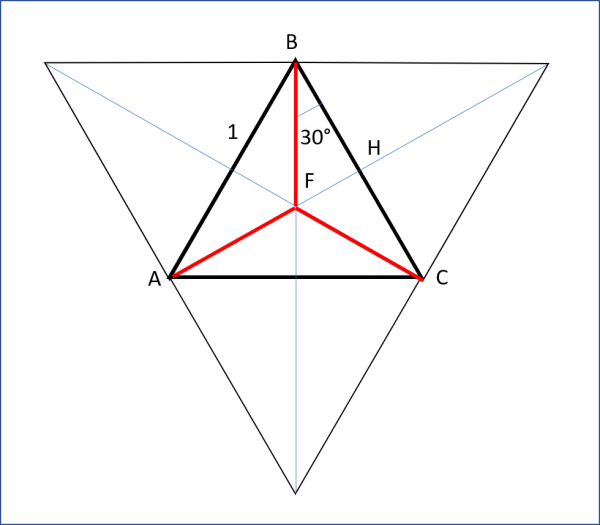
La loro lunghezza totale si calcola facilmente, considerando il triangolo BFH che è rettangolo con un angolo di 60° e uno di 30°. Si ha, perciò:

BF² = BH² + HF²

BF² = 1/4 + BF²/4

3BF²/4 = 1/4

BF = 1/√3

Il percorso completo autostradale p è uguale a tre volte BF, per cui:

p = 3/√3 = √3 = 1.732

La somma di due lati è nettamente maggiore essendo uguale a 2.

La dimostrazione del valore minimo di questa lunghezza è data da Fabrizio nei commenti. La sua conclusione riguardo all'angolo uguale a 30° è corretta, ma il fatto che l'angolo sia di 30° corrisponde, più correttamente, a dire che l'angolo tra le linee che partono dal punto di Steiner è di 120°. In un triangolo acutangolo il punto di Steiner non cambia e quindi l'angolo di 30° resta sempre uguale a se stesso.

Passiamo al quadrato (sempre di lato unitario)...

I punti di Steiner devono essere 2 e si può ottenere la loro posizione anche per via grafica muovendo i punti di Steiner con i loro tre segmenti autostradali "incollati",  facendo in modo che siano raggiunti i tre vertici.

Si ottiene la Fig. 4.

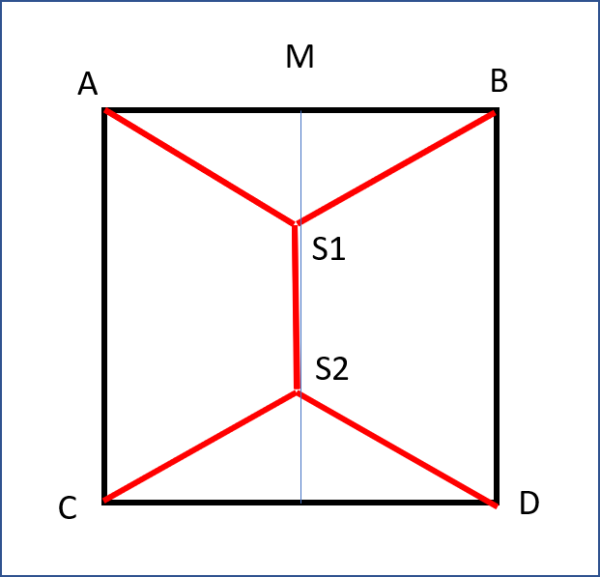
Consideriamo il triangolo MS1B. Dato che S1 è un punto di Steiner l'angolo in B è di 30° e quello in S1 di 60°.

Possiamo scrivere:

MS1² = BS1² - MB²

MS1² = 4 MS1² - 1/4

3MS1² = 1/4

MS1 = 1/(2√3)

da cui

BS1 = 2/(2√3) = 1/√3

Il percorso autostradale completo è, allora:

p = 4BS1 + (1 - 2MS1) = 4/√3 + 1 - 2/(2√3) = (3 + √3)/√3 = √3 + 1  = 2.732

Decisamente minore del perimetro meno un lato (p_L =3) o della somma delle due diagonali (p_D = 2√2 = 2.824)

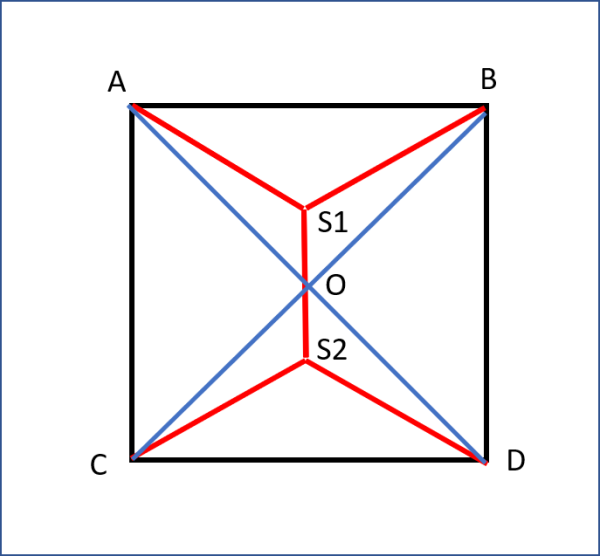
Non cerchiamo nemmeno la dimostrazione analitica, dato che basta guardare la Fig. 5 e considerare i due triangoli AOB e COD. Considerare loro due come poligoni separati equivale perfettamente a considerare il quadrato ABCD, in quanto i punti da congiungere sono esattamente gli stessi. Tuttavia, per entrambi i triangoli si può applicare la strategia operativa di Stein e, di conseguenza, il percorso minimo per il quadrato deve essere la somma dei due due percorsi minimi dei triangoli.

Un po' più complicata la faccenda riguardante il pentagono...

Sappiamo che il numero di punti di Steiner da considerare è tre (con i loro segmenti a 120° l'uno dall'altro). Piazziamo subito il primo punto partendo dal vertice in alto, in modo da avere una base simmetrica (Fig. 6, a sinistra).

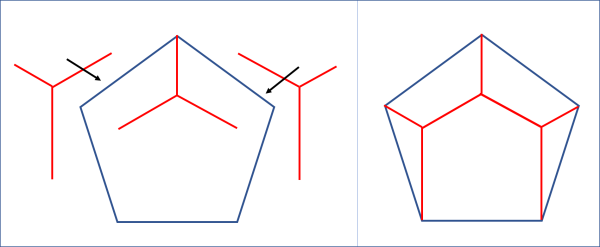
Muoviamo gli altri due punti in modo che riescano a raggiungere i rimanenti 4 vertici (a due a due), sovrapponendo un segmento a quelli laterali del punto precedente. In tal modo abbiamo raggiunto tutti i punti del pentagono utilizzando esattamente tre punti di Steiner (Fig. 6, a destra).

Non ci resta che determinare la lunghezza del percorso rosso di Fig. 7

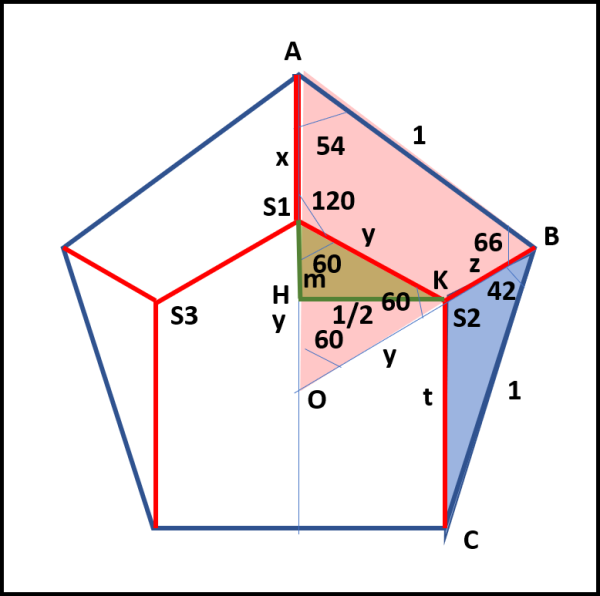
Chiamiamo x, y, z e t i quattro segmenti che ci servono per calcolare il percorso minimo di Steiner e identifichiamo i triangoli rosa (AOB), verde (S1HS2) e azzurro (KBC).

Il triangolo S1HS2 è rettangolo con un angolo di 60°, quello in S1, in quanto uguale a 180° - 120°. Possiamo, perciò scrivere:

y² = m² + 1/4

m = y/2

y² = y²/4 + 1/4

y² - y²/4 = 1/4

3/4 y² = 1/4

y  = 1/√3 = 0.5774

Consideriamo, ora, il triangolo rosa AOB. I suoi angoli sono noti, in quanto quello in A è la metà dell'angolo interno di un pentagono regolare, ossia 54°. Quello in O è 60° e, di conseguenza, quello in B è di 66°.

Applichiamo il teorema dei seni

(x + y)/sen(66) = 1/sen(60)

x + y =  sen(66)/sen(60) = 0.9135/0.8660 = 1.0549

x = 1.0549 - 0.5774 = 0.4775

Applichiamo nuovamente il teorema dei seni allo stesso triangolo

(z + y)/sen(54) = 1/sen(60)

z + y = sen(54)/sen(60) = 0.8090/0.8660 = 0.9342

z = 0.9342 – 0.5774 = 0.3566

Non ci resta, adesso, che calcolare t e lo facciamo applicando il teorema di Carnot al triangolo azzurro

t² = 1 + z² -2 z cos(42) = 0.1272 + 1 – 0.7132 ∙ 0.7431 = 0.5972

t = 0.7728

Il percorso p totale è dato da:

p = 2y + 2z + x + 2t = 3.8911

Non ci resta che considerare l'esagono regolare...

In questo caso la risposta è facilissima: i punti di Steiner coincidono con i vertici e quindi il percorso più conveniente è lungo i lati stessi del poligono. Il percorso minimo diventa allora:

p = 5

Per valori superiori dei lati , continua a valere la somma di essi meno uno, ma, come detto, il problema generale risulta insoluto.

Va bene, ci siamo divertiti un po' e abbiamo preparato un piano autostradale che sembrerebbe ottimale, ma, dato che non necessita di "mazzette", ... non se ne farà niente!

Un bravo al "solito" Fabrizio che con calma è arrivato alla soluzione.