QUIZ:Un quadrilatero sbilenco e una sfera. **/******
Sto cercando disperatamente di proporre dei quiz che siano risolvibili anche dal cellulare, quindi privi di disegni e calcoli complessi. Lasciamo per un pò perdere poi l'esposizione romanzesca, per essere più precisi, come vuole la matematica (anche perchè in questo caso non avrei idee per scriverla). Abbiamo a che fare con una figura sbilenca e una simmetricamente perfetta; cosa succederà ai punti di contatto se si tenta di incastrare una nell'altra?
Formuliamo quindi il nostro quiz in modo strettamente matematico-geometrico:
Si abbia un quadrilatero sghembo nello spazio (attenzione, nello spazio non nel piano). Questa definizione potrebbe generare delle ambiguità; usiamo la definizione formalmente esatta (tratta da WIKIPEDIA) :
" un quadrilatero sghembo è una poligonale nello spazio formata da quattro segmenti, che non è contenuta in un piano. Un quadrilatero sghembo non è quindi propriamente un quadrilatero" (per quadrilatero si intende al solito un quadrilatero piano).
Supponiamo che i suoi lati, o bordi, siano tangenti ad una sfera. Dimostrare che tutti i punti di tangenza si trovano nello stesso piano. Ancora un quiz dedicato alla semplicità, per quanto complesso possa apparire. E' per questo che come difficoltà sono stati messi **/****** asterischi; se si "imbrocca" la strada giusta può essere risolto con pochi ragionamenti. Altrimenti, penso sia molto dura.






34 commenti
butto l'amo... per tre punti non allineati passa un solo piano e quindi si determina un.... ecc. ecc. Una su mille ce la fa, come diceva Morandi! Nessun calcolo, come dice Umberto...
Non capisco...
Il commento che segue non dimostra che tutti i quattro punti di tangenza tra una sfera ed un quadrilatero sghembo qualsiasi si trovano su uno stesso piano, ma propone alcune osservazioni che potrebbero essere utili.
Ragionando sul piano si sa che non tutti i quadrilateri possono essere circoscritti ad un cerchio, occorre che la somma di due lati opposti sia congruente alla somma degli altri due, ad esempio sono circoscrittibili i quadrati ed i rombi.
Nelle tre dimensioni la circonferenza diventa una sfera e i lati del quadrilatero diventano dei piani tangenti.
Un pallone contenuto in una scatola a forma di cubo (di lato pari al diametro del pallone) può essere un esempio semplice per iniziare il ragionamento.
Lasciando da parte il fondo e il coperchio della scatola, al centro delle quattro pareti laterali del cubo, abbiamo altrettanti punti di tangenza con la sfera.
Disegno una diagonale su una faccia, salendo dall'angolo in basso a sinistra fino all'angolo in alto destra, poi la diagonale della faccia adiacente, in discesa, e poi, proseguendo sulla terza faccia, la diagonale che sale e sulla quarta la diagonale che scende, (si ricongiungerà al punto di inizio).
Ho così tracciato un quadrilatero sghembo che ha quattro punti di tangenza con la circonferenza.
E' evidente che i quattro punti si trovano su un piano, il piano del cerchio massimo orizzontale (l'equatore) della sfera.
Se uno dei quattro punti si scostasse dal piano non sarebbe possibile mantenere il contatto con ambedue i lati adiacenti e il quadrilatero resterebbe "aperto".
Ora immaginiamo di prendere un foglio quadrato e di disegnare in esso il cerchio inscritto. Ripieghiamo il foglio lungo una diagonale tenendolo posato sul tavolo, poi dispieghiamolo in modo da riaprirlo finché sia completamente adagiato sul piano. Nel fare questo movimento possiamo immaginare la superficie sferica generata dalla mezza circonferenza durante la rotazione e interpretare i bordi del foglio come i lati di un quadrilatero sghembo.
In ogni posizione questi lati saranno tangenti alla sfera. I due punti di tangenza che sono in movimento resteranno costantemente allineati con gli altri due punti fissi, su uno stesso piano. Dato che i due punti si muovono insieme non si crea nessuna rottura dei collegamenti tra i lati. Il quadrilatero resterà sghembo fino al momento in cui il foglio tornerà ad essere completamente disteso sul piano.
Potremmo rifare la stessa operazione con un foglio a forma di rombo invece che a forma di quadrato.
Si tratta ora di vedere se è possibile generalizzare questi esempi prendendo in considerazione quadrilateri meno "simmetrici" in cui in ogni caso la somma di due lati opposti sia congruente alla somma degli altri due.
Maurizio, ti ringrazio per le tue considerazioni molto sensate, che
senz'altro possono essere molto utili
Mi ero limitato ad accennare a come si costruisce una sfera inscritta (e quindi anche circoscritta) a un quadrilatero sghembo. Tutto lì... comunque, lasciamo il campo aperto ai lettori e torno ad Archimede...
capisco.. ricordo però che il quadrilatero e la sfera sono dati del problema. In ogni caso mi aspetto delle risposte, non dei suggerimenti, come è usuale in quiz. Volevo poi chiarire un fatto; si può rispondere a questo quiz come meglio si crede, sia con ragionamenti semplici che con calcoli e disegni complessi. Parlavo per chi non ha la possibilità di inserire disegni o scrivere formule complesse senza usare latex.
comunque la sfera è una e una sola, da cui nascono ovvie conseguenze... OK... non disturbo più
non è questione di disturbare.. se hai una risposta pubblicala, io ne sono ben lieto. Ma se parli per enigmi non posso capire.
domanda: il quadrilatero è sghembo, ma come mai la somma dei lati opposti è uguale? Condizione per essere un quadrilatero che sta su un piano? Dove sbaglio? vado un po' di fretta...
Che dipenda dalle simmetrie presenti nei casi particolati degli esempi?
Un altro caso banale è quello di una circonferenza inscritta in un foglio a forma di triangolo equilatero.
Quando piego il foglio seguendo la linea di una altezza, il triangolo piano diventa un quadrilatero sghembo in cui la somma dei lati opposti è la stessa.
Due punti di tangenza che ha con la sfera inscritta sono coincidenti. Questo implica che i quattro punti diventano tre e, come si diceva, per tre punti passa un piano.
Resta da vedere se esistono quadrilateri in cui è inscrivibile una sfera e che abbiano lati che non rispettino la condizione citata per i quadrilateri piani circoscittibili.
sono i punti di tangenza che stanno su un piano, non il quadrilatero che è sghembo
Accidenti... all'inizio ero convinto che la domanda fosse un'altra... Va beh... cose che capitano.
La figura che segue dovrebbe essere sufficiente...
I punti ABC stanno su un piano e così pure i segmenti in rosso. I punti BCD stanno sul un altro piano e così pure i segmenti verdi. Ma quello rosso e quello verde di sinistra stanno anche sul piano di ABD e così dall'altra parte. Tutto il quadrilatero deve stare su un piano...
Boh... non posso fare figure migliori, dato che stiamo sbaraccando mezza casa... Però dovrebbe funzionare dato che sappiamo che la linea blu è un segmento continuo e anche quella marrone
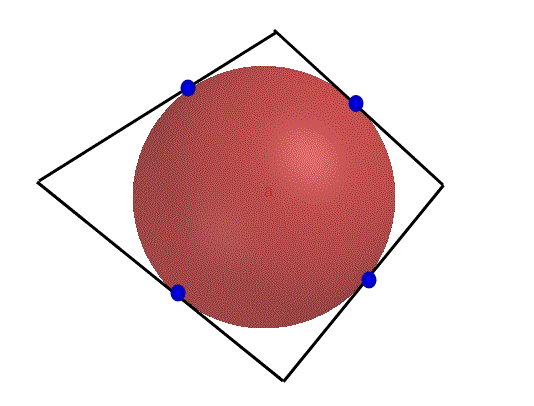
Avevo preparato questa figura che potrebbe corrispondere in parte a quanto detto da Enzo.
Si vede che il quadrilatero sghembo ha come punti di tangenza con la sfera punti che si trovano tutti sullo stesso piano. Se uno di questi punti non fosse sul piano dagli altri non si realizzerebbe la chiusura del quadrilatero sghembo.
caro Mau, direi che siamo sulla stessa linea...
Forse si potrebbe applicare anche la somma dei lati opposti dato che vi sono triangoli isosceli, ma non mi sembra ci sia bisogno...
Cari Enzo e Umberto, mi chiedo se il procedimento che ho illustrato con la mia figura possa valere anche se il piano non è equatoriale, direi di si ma vorrei il vostro parere...
vedo che avete scelto la via grafica.. Però io non posso rispondere alle vostre domande..é un quiz! Poi alla fine tiriamo le somme
Giusto. Allora aggiungo qualche considerazione sulla figura che ho proposto...
Visto dall'alto, il cerchio equatoriale è circondato dal quadrilatero piano. Posso immaginare la sfera inserita in un prisma che ha come base il quadrilatero.
Se invece il cerchio è parallelo a quello equatoriale, posso pensare che la sfera sia inserita in una piramide. I punti di tangenza sono i punti di contatto tra sfera e facce della piramide. Questi punti si trovano sullo stesso piano che fa da base alla piramide. Il quadrilatero piano circoscritto è proprio la base della piramide.
Sullo sviluppo della superficie laterale della piramide posso operare nello stesso modo visto in precedenza, ossia sulla linea spezzata (prima era rettilinea) che rappresenta lo sviluppo del perimetro del quadrilatero piano (la base) , andrò ad eseguire la successione di rotazioni di ciascun segmento attorno al suo punto di tangenza ed otterrò il tracciato del quadrilatero sghembo che ha gli stessi punti di tangenza individuati su quello piano. I vertici di questo quadrilatero saranno alternativamente al di sopra e al di sotto del piano di base della piramide, lungo i suoi spigoli inclinati.
La chiusura del quadrilatero sghembo si realizza anche in questo caso per il fatto che tutti i punti di tangenza sono sul medesimo piano.
Con maggiore tranquillità, allego una figura che, secondo me, dovrebbe essere risolutiva:
I punti del quadrilatero sghembo sono P,M,N,O. P,M,N stanno sul piano a e P,N,D stanno sul piano b. I punti di tangenza sono A,B,C e D. Mettiamoci nel punto N da cui si tirano le tangenti alla sfera. Ne segue che NB = NC. La stessa cosa capita per P, ossia PA = PD. Per maggior chiarezza mettiamoci nel piano perpendicolare ad a e b (figura a destra). AP = DP e BN = CN, ca dui segue che CB è parallelo ad AD. Per una coppia di segmenti paralleli passa un piano, che nel nostro caso è individuato da ABCD.
mmm.. non sono un granchè in geometria euclidea, ma praticamente la conseguenza del tuo ragionamento è che qualsiasi sia il quadrilatero sghembo P,M,N,O AD e CB (segmenti che collegano i punti di tangenza adiacenti )sono sempre paralleli? Mi sembra strano anche se non posso escluderlo direttamente.
Beh... per la ovvia deduzione che le tangenti a una sfera tirate da un punto formano segmenti uguali... BNC sta su un piano. Attenzione a non confondere le rette parallele con le loro proiezioni (che comunque stanno sempre sullo stesso piano).
ok, per adesso non dico altro (anche perchè se è corretto lo sai meglio di me)
Aspetto altre risposte; e i nostri amici dove son finiti?
I segmenti CB e AD nella figura di destra sono le proiezioni laterali dei segmenti CB e AD nela figura di sinistra.
Sono questi segmenti-proiezioni ad essere paralleli, mentre non lo sono in generale (e in particolare in questo esempio) i segmenti CB e AD in pianta.
Mi sembra che il ragionamento funzioni.
Grazie del contributo Maurizio
darò la soluzione (mia) del quiz probabilmente domenica. Quindi c ' ê ancora tempo. Dove sono finiti i risolutori più abili? Quelli che di solito sono in grado di capire anche gli enigmi più complessi? Il quiz è Troppo banale o troppo difficile, oppure di scarso interesse?
quiz molto interessante ma fuori dalla mia portata..
Io avevo intenzione di arrivarci attraverso la geometria analitica dello spazio. Dato il quadrilaero sghembo, di vertici dati A, B, C, D, considero un punto genrico su ciascuno dei 4 lati, che chiamo E, F, G, H. Considero la sfera passante per tali 4 punti. Poi considero per ciascuno dei 4 lati del quadrilatero il fascio proprio di piano avente sostegno la retta per i due vertici del lato. L'equazione di tale fascio proprio di piani , note le coordinate dei vertici (dato del problema) contiene la variabile k , variando la quale varia il piano del fascio. Ora vado a prendere, di tale fascio di piani, quello tangente alla sfera nel punto preso prima in considerazone su quel lato. Nel caso del lato AB, il punto E. In pratica, trovo il valore di k che mi da il piano del fascio di sostegno AB e tangente in E alla sfera. Ripeto il ragionamento per i 4 lati, ottenendo le coordinate dei 4 punti di tangenza. Ora, di tale 4 punti ne considero 3 e prendo l'quazione del piano pasante per tali 3 punti (per 3 punti non allineati passa uno e un solo piano). Infine, prendo le coordinate del 4 punto di tangenza e le sostituisco all'equazione del piano passante per i primi 3 punti. E mi accorgo che ottengo un'identità. Cioè , le coordinate del quarto punto soddisfano anch'esse l'equazione del piano passante per gli altri e. Quindi , anche il quarto punto appartiene allo stesso piano degli altri. CVD. Mi ero anche messo a scrivere il procedimento analitico, ma viene fuori una mostruosità di calcoli , meglio evitare...
Grazie Arturo. Ti chiedo troppo per una figura solo esplicativa? Forse così gli altri lettori possono capire meglio il ragionamento. Di solito le tue figure parlano da sole.
Caro Arturo il tuo ragionamento è convincente e la tua affermazione che i calcoli analitici diventano soverchianti (immagino quanto) conferma quanto premesso da Umberto riguardo alla difficoltà variabile del quiz a seconda della impostazione scelta.
@Umberto
Spero renda sufficientemente bene l'idea. Il piano che si vede in figura è quello di sostegno AB e tangente in H alla sfera.
Ok grazie
Ci provo anche io.
Considero 3 dei 4 punti di tangenza. Per 3 punti passa sempre un piano.
Per ragionare più agevolmente posiziono la sfera in modo che questo piano sia orizzontale.
Una tangente, comunque orientata, si trovano sul piano tangente al punto. Di conseguenza, l’intersezione di due tangenti si trova sulla intersezione dei due piani tangenti. Per come ho orientato la sfera, questi piani hanno la stessa inclinazione rispetto al piano orizzontale. La loro intersezione è quindi simmetrica rispetto ai due punti di tangenza, cioè un qualsiasi punto di questa retta è equidistante dai due punti di tangenza.
[caption id="" align="aligncenter" width="253"] Vista dall'alto[/caption]
Vista dall'alto[/caption]
Questo comporta che le due rette tangenti abbiano la stessa inclinazione. Dal punto di intersezione, per arrivare ai punti di tangenza devono salire (o scendere) della stessa altezza nella stessa distanza. Questo vale per tutte le 3 rette tangenti ai punti che ho selezionato.
Ma varrebbe anche per il 4° punto se fosse comunque posizionato alla stessa altezza degli altri 3. Verrebbe sia rispetto al 3° punto, sia rispetto al 1° punto. Quindi sembra possibile posizionare il 4° punto sullo stesso piano degli altri 3.
Questa posizione del 4° punto sembra possibile, ma è necessaria?
Non so!!
Tentativo di visualizzare anche i piani tangenti nella seconda figura con vista dall'alto e di lato.
Vedo adesso.
Grazie fabrizio