Ecco la soluzione del tappo multiuso. Un po' di ricordi delle proiezioni ortogonali di un solido, come ha detto Fabrizio, e il tappo si costruisce quasi da solo...

Innanzitutto rispondiamo compiutamente alle "solite" polemiche di Frank... Lui dice: "Per quale liquido? Quanto deve aderire alle pareti? Che pressione deve tenere? Che materiale sono le pareti? Qualsiasi materiale o solo di tipo idoneo all'uso alimentare? ecc ecc ecc." Ciò che chiede non c'entra niente col problema proposto. Quello che ci interessa è la forma geometrica che aderisca perfettamente alle pareti. A seconda del liquido, della sua temperatura, del materiale del tubo o quello che volete, si userà il materiale più adatto  per il tappo. Certo non lo faremo di plastica che si fonde se il liquido è bollente. E nemmeno lo costruiremo di cartone se esce del liquido qualsiasi. Lo spirito del quiz era solo di carattere geometrico.

Passiamo alla soluzione, rispondendo alla prima domanda:

Le sezioni del tubo devono essere:

un quadrato di lato L

un cerchio di diametro L

un triangolo isoscele di base L e altezza L

Ossia qualcosa come quello che è rappresentato nella Fig. 1 .

Il nostro tappo deve, perciò, avere le sue tre sezioni (visione dall'alto, di lato e di fronte) uguali  alla Fig. 2.

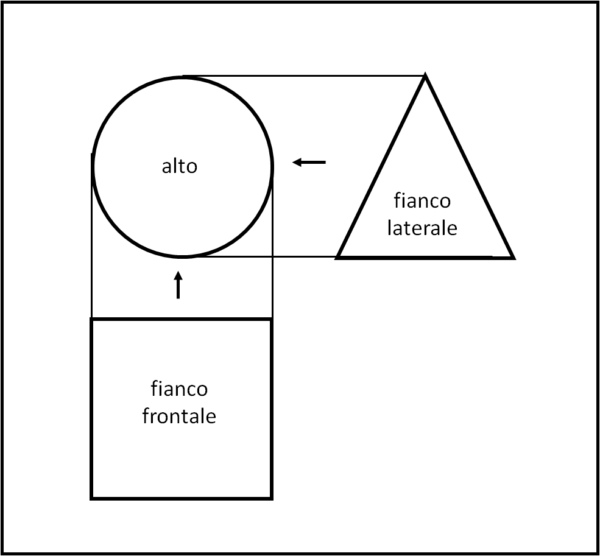
Difficile? Nemmeno per sogno...

Prendiamo un cilindro che abbia l'altezza uguale al diametro del cerchio di base. Esso è perfetto per la visione dall'alto e per quella frontale (Fig. 3).

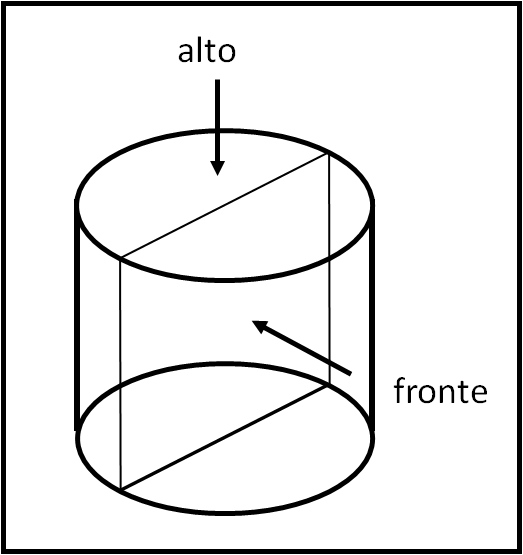
Adesso non ci resta che tagliarlo con un piano che passi per un diametro del cerchio superiore del cilindro e che tocchi un solo punto del cerchio di base inferiore (Fig. 4).

Facciamo lo stesso taglio dal lato opposto, utilizzando sempre lo stesso diametro della base superiore. La vista di fronte continua a darci un quadrato, ma quella laterale ci dà un bel triangolo e poco importa che sia "panciuto" verso chi lo guarda: la sezione è un triangolo come quello che volevamo. La Fig. 5 (quella di Fabrizio) è perfetta per una visione del tappo in tre dimensioni.

E' anche immediato capire che curva è quella lasciata dal taglio... non ve lo dico nemmeno... basta ragionarci un attimo...

Peccato, il nostro Frank abilissimo con torni di alta precisione, avrebbe potuto fabbricarlo in metallo (o in legno) e mostrarcelo. Comunque... è sempre in tempo!