Quiz: un numero molto lungo **....

29/05/20

Quiz: un numero molto lungo **....

Categorie: Matematica Tags: Scritto da: Umberto Cibien Commenti:7

Un quiz a prima vista poco interessante,  che non ha risvolti teorici o pratici .Consideriamolo come un giochetto per chi ama dilettarsi con numeri  e potenze. Potrebbe  essere molto utile per la soluzione l'applicazione di una formula  scoperta da quello che per me è stato il più abile fisico-matematico di tutti i tempi (questa naturalmente è una mia opinione.) Ma  veniamo al dunque;l'enunciato è semplicissimo; dato il numero:

\dpi{200} 125^{100}

dire quante siano le sue cifre.

A scanso di equivoci, 12789 è un numero a cinque cifre. Naturalmente il sistema numerico adottato è quello decimale. Chiaramente non basta eseguire il calcolo con la calcolatrice, che supponiamo non avere a disposizione. Bisogna esporre un ragionamento e/o dei calcoli, seppur semplici.

Articoli correlati

7 commenti

  1. Maurizio Bernardi
    29/05/2020 at 14:12

    Posso scrivere 125^100 = 10^x  e uguagliare i logaritmi :   100 log(10)125 = x log(10)10 = x

    x=    300 log(10) 5

    Non posso usare la calcolatrice per trovare il valore del log(10)5 e non ricordo lo sviluppo in serie della funzione, però ricordo a memoria che il log(10) 2 vale 0,30103,  quindi calcolo:  log(10)5 =  1 - 0,30103 = 0,69897    e lo inserisco nel calcolo di x.

    x= 300*0,69897 = 209,691

    N=125^100   = 10^0,691 * 10^209   è un numero composto da 210 cifre.

     

  2. Umberto
    29/05/2020 at 17:58

    Il risultato è certamente esatto.. ma non si dovrebbe fare ricorso alla calcolatrice, o alle tavole dei logaritmi. L'ultima cosa mi sono dimenticato di scriverla. Vediamo se qualcuno riesce a trovarlo in modo autonomo. Comunque complimenti; logaritmo a parte se stato rapidissimo.

  3. Fabrizio
    30/05/2020 at 11:12

    Una possibilità senza logaritmi. Senza calcolatrice ci vuole molta pazienza.

    125^{100}=(5^3)^{100}=\left ( \frac{10^3}{2^3} \right )^{100}=\frac{10^{300}}{(2^{10})^{30}}=\frac{10^{300}}{(1024)^{30}}<\frac{10^{300}}{(1000)^{30}}=10^{210}

    Quindi il numero di cifre è  minore di 211. Poichè 1024 è molto vicino a 1000 posso suppore che sia proprio 210. Per dimostrarlo dovrei dimostrare che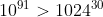    10^{91}>1024^{30}.

    Ci sono riuscito solo parzialmente in questo modo:

    10^{91}>(1000+24)^{30}=\sum_{0}^{30}\binom{30}{i}10^{3(30-i)}24^i    che equivale a

    1>\sum_{0}^{30}\binom{30}{i}\frac{10^{90}10^{-3i}}{10^{91}}24^i=\sum_{0}^{30}\binom{30}{i}\frac{24^i}{10^{1+3i}} che espansa diventa

    1>\frac{1}{10}+\frac{30\, 24}{10^4}+\frac{30\,29\,24\,24}{2\,10^7}+....=0,1+0,072+0,025056+....

    La somma di questi primi 3 termini da circa 0,197, manca circa 0,803 per arrivare ad 1 con la somma dei 28 termini successivi. Anche se fossero tutti come l'ultimo dei 3, non ci si potrebbe arrivare (0,025*4*7=0,7). Qui assumo che i termini siano decrescenti, senza dimostrarlo.

    Quindi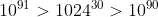     10^{91}>1024^{30}>10^{90} di conseguenza 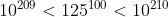10^{209}<125^{100}<10^{210}  vale a dire

    210\leq Numero\,di\,cifre< 211\; \; \rightarrow Numero\,di\,cifre=210

     

     

     

     

     

  4. Umberto
    30/05/2020 at 11:54

    Sì è proprio quello che intendevo nel testo: Newton e il suo binomio. Più o meno è quello che ho fatto io. Complimenti Fabrizio mi hai risparmiato di scrivere la soluzione. Comunque se qualcuno ha qualche altro metodo o idea ben venga.  Si può pensare anche alla stima del logaritmo di Maurizio..

  5. maurizio bernardi
    30/05/2020 at 22:12

    Un modo, non generale come quello proposto da Fabrizio, basato sul binomio di Newton,  ma utilizzabile in questo quiz senza ricorrere al logaritmo di 2 ( che ricordo per la sua   parte decimale (30103) , simpaticamente palindroma) è quello di calcolare dapprima il valore di 5^10.

    Il metodo che preferisco per calcolare questi valori è dividere per 2 il risultato precedente, escludendo l’ultima cifra, e affiancare 25  al risultato della divisione.   Inizio da 125, ossia 5^3.

    5^3                  2:2=        1                               125

    5^4                12:2=        6                               625

    5^5               62:2=       31                             3125

    5^6            312:2=      156                          15625

    5^7          1562:2=     781                           78125

    5^8          7812:2=   3906                         390625

    5^9       39062:2=   19531                     1953125

    5^10   195312:2=   97656                    9765625

    Fin qui ce la siamo cavata con 8 divisioni per 2, un po’ noioso ma non difficile.

    Quindi, elevando a 10 il numero 5, abbiamo un numero di 7 cifre. Possiamo scriverlo così

    0,9765625 * 10^7

    Elevando 30 volte questo numero otteniamo il risultato:

    0,9765625 ^30 * 10^210

    Il numero di cifre del risultato  sarà 210 solo a condizione che 0,9765625 ^30 non sia inferiore a 0,1, perché sotto questa soglia si perderebbe una cifra.

    Valutiamo l’entità del decadimento per un valore più piccolo di 0,9765625, ad esempio 0,97

    Ad ogni moltiplicazione si perde il 3%  (sul valore precedente)

    0,97 – 0,97*3/100 =   0,97 - 2,91/100 =  0,9700-0,0291

    0,9409 – 0,9409*3/100 = 0,9409 – 2,8227/100 = 0,940900 – 0,028227 = 0,912673

    0,912673-  0,912673*3/100 =  0,912673 - 2,738019/100 =   0,91267300 -  0,02738019 =   0,88529281

    Dopo 3 passi siamo scesi da 0,97 a 0,885 (esagerando) con una riduzione di 0,085 dal valore di partenza.

    Anche se questa perdita, cumulata sulle prime 3 riduzioni, restasse costante, moltiplicandola per 10 volte otterremmo, dopo 30 riduzioni del valore iniziale 0,97, la riduzione totale di 0,85 ed un valore residuo maggiore di 0,1.

    Quindi, il valore di 0,9765625^30 non è inferiore a 0,1   e possiamo dire che il numero di cifre di 125^100 è 210.

  6. Oreste Pautasso
    30/05/2020 at 22:22

    Incidentalmente... Dire che 5^10 vale (quasi)  10 ^7 equivale a dire che

    Log(10)5 = 0,7 (quasi)

     

  7. Umberto
    31/05/2020 at 06:36

    ok Maurizio, grazie dell'integrazione

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.