Questo articolo è stato inserito nella pagina d'archivio dedicata alla Disuguaglianza di Bell

LA DISUGUAGLIANZA DI BELL
L'oggetto della disuguaglianza di Bell e il suo valore per la teoria standard

Nell’articolo precedente siamo partiti dalla configurazione di prova utilizzata per misurare le grandezze che sono oggetto  disuguaglianza di Bell.

Figura 4.1

Analizzando questo esperimento con l’interpretazione standard della MQ, siamo arrivati a calcolare le probabilità delle quattro combinazioni dei possibili risultati quando la sorgente emette coppie di fotoni entangled.

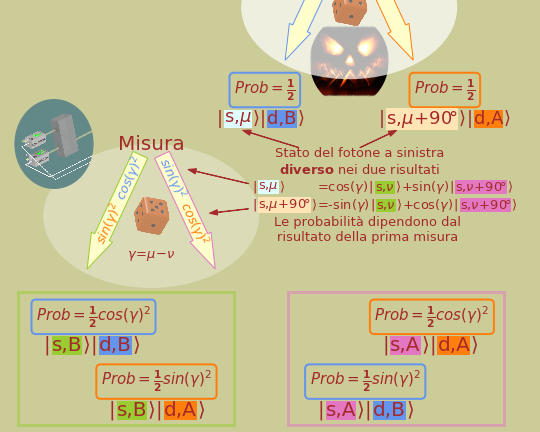
Tabella 5.1

In questo risultato si nascondono alcune cose strane.

Esaminiamo questi risultati dal punto di vista di chi sorveglia i due apparati di misura mentre si svolge l'esperimento. L'addetto allo strumento di destra vede che viene prodotta una sequenza casuale di risultati (A e B) uniformemente distribuita tra i due risultati.

Lo vediamo nella tabella sopra in termini di probabilità del risultato dopo la prima misura che è 1/2 per ciascuna delle due possibilità. Notate che il risultato non dipende dalla posizione del cristallo. Lo sperimentatore non ha modo di influire sul risultato. Potrebbe ruotare l'apparato di misura a piacere e il risultato rimarrebbe invariato. Sempre il 50% di A ed il 50% di B.

Il calcolo delle probabilità dei risultati visti dallo sperimentatore a sinistra richiede una piccola elaborazione.

Tabella 5.2

Quindi, anche l'addetto allo strumento di sinistra vede che il suo strumento produce una sequenza casuale di A e B uniformemente distribuita tra i due risultati. Anche lui non riesce a modificare il risultato ruotando il suo apparato.

Tabella 5.3

La sequenza dei risultati delle misure non permette a nessuno dei due sperimentatori di capire  come sia stato impostato l'apparato di misura remoto o anche eventuali variazioni della sua posizione. I due sperimentatori neanche possono capire se la misura remota sia stata effettuata, né possono modificare i risultati delle misure locali o remote agendo sul proprio apparato. Per questo, l'azione istantanea a distanza tra i due fotoni non può portare informazioni tra i due sperimentatori. Questa incapacità viene generalmente presa come prova che questo fenomeno non contraddice la relatività.

Solo il confronto delle due sequenze dà informazioni su come i due apparati siano stati posizionati. Nella nostra schematizzazione di figura 5.1, la misura che ci interessa è effettuata dal contatore di coincidenze. Il contatore registra una coincidenza se i fotoni delle stessa coppia sono rivelati dai contatori marcati nello stesso modo (A a destra e A a sinistra o B B). Invece registra una discordanza se sono rivelati da contatori marcati in modo diverso (A B o B A).

Per fare il confronto occorre fare arrivare le due sequenze in un punto comune. Il punto dove abbiamo collocato il contatore di coincidenze. Questi trasferimenti avvengono a velocità al più uguale a quella della luce. Perciò, qualsiasi informazione si possa ricavare dal confronto è considerata compatibile con la relatività.

Vediamo ora le previsioni che l'interpretazione standard dà delle probabilità che il contatore di coincidenze registri una coincidenza o una discordanza.

Tabella 5.4

Da notare che le probabilità dipendono solo dalle posizioni dei cristalli nei due apparati. Più precisamente dalla differenza tra gli angoli μ e ν.

Vediamo alcune previsioni per diversi posizionamenti dei due cristalli.

Tabella 5.5

Una grandezza che ci dà una sintesi dei risultati registrati è il loro valore medio. Per calcolare il valore medio però occorrono dei risultati numerici. Li otteniamo assegnando alla coincidenza il valore +1 e alla discordanza il valore -1. La media di questi risultati, che identifichiamo con E, è normalmente denominata coefficiente di correlazione.

Per esemplificare il significato di questa grandezza possiamo immaginare una slot-machine un po’ particolare, una slot machine quantistica. Si vince 1€ se il risultato è concorde. Si perde 1€ se il risultato è discorde.

Tabella 5.6

Il valore della grandezza E è proprio la vincita media (perdita media se negativa) per un particolare configurazione della differenza tra μ e ν.

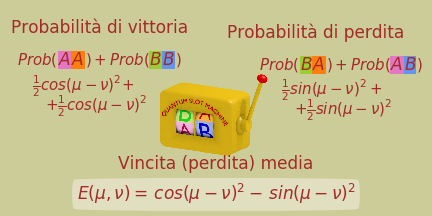
Tabella 5.7

Faccio alcuni esempi riprendendo quelli fatti sopra.

Tabella 5.8

Abbiamo così ottenuto la previsione della grandezza E secondo l'interpretazione standard per ogni coppia di angoli ν e μ.

Tabella 5.9

Partiamo da questo punto ed iniziamo a scoprire il contributo, direi geniale, di J.S.Bell.

Paragonerei J.S.Bell ad un investigatore e le diverse interpretazioni della MQ a due testimoni di un fatto. L’investigatore riceve dai testimoni due diverse descrizione degli eventi che si sono susseguiti. Entrambe le descrizioni appaiono plausibili.

Per capire l’affidabilità dei testimoni, l’investigatore inizierebbe a fare a ciascun testimone una serie di domande apparentemente innocue, cercando di fare emergere delle incongruenze nelle loro descrizioni.

Le domande che ha escogitato J.S.Bell riguardano proprio la grandezza E vista sopra. J.S.Bell chiede a ciascuna delle interpretazioni il valore di questa grandezza per quattro coppie di valori degli angoli ν e μ, le combinazioni di due valori degli angoli per ciascun apparato di misura. Poi fa una semplice operazione con i quattro risultati per arrivare ad un singolo numero.

La risposta la possiamo ottenere facilmente per l’interpretazione standard. Nella tabella sotto elenco questi valori per le due coppie di angoli che sono stati giudicati migliori per la sperimentazione: μ= 0° o 45° e ν= 22,5° o 67,5°.

Tabella 5.10

Ci sono diverse grandezze che sono state definite negli articoli di Bell e di altri autori che hanno seguito ed approfondito l'idea di Bell. Quella riportata sopra credo sia la più semplice rispetto ad altre che sono più restrittive e più generali. Questa grandezza è utilizzata da Alain Aspect in alcuni suoi articoli per spiegare i suoi esperimenti. Alain Aspect è un fisico sperimentale che ha dato un contributo notevole, forse il maggiore, alla realizzazione degli esperimenti che hanno messo a confronto le teorie con la disuguaglianza di Bell. Per maggiore semplicità ho inserito da subito i valori degli angoli che sono risultati i migliori per effettuare gli esperimenti.

I calcoli della tabella precedente possono essere fatti abbastanza facilmente anche con la calcolatrice di qualche smartphone o con un foglio di calcolo. C'è anche una relazione trigonometrica che può essere utilizzata e porta ad un risultato più compatto. Tabella 5.11

Così abbiamo ottenuto il valore della grandezza S come previsto dalla interpretazione standard. L’obiettivo che abbiamo è quello di confrontare questa previsione del valore di S con quella che potremmo ottenere da una teoria che rinuncia al quell'inquietante effetto istantaneo a distanza che prevede l’interpretazione standard. Un teoria che viene definita locale.

A questo punto abbiamo un problema!

L’interpretazione standard è una teoria che produce previsioni ben definite. Infatti applicandola siamo arrivati ad un numero ben definito. La teoria alternativa locale invece non esiste. Lo scopo della disuguaglianza di Bell è proprio quello di sondare se una teoria di questo tipo possa esistere.

Come fare un confronto tra una previsione ben definita ed una che non sappiamo come calcolare? Qui interviene John S. Bell con la sua felice intuizione.

La risposta a questa domanda la vedremo nel prossimo articolo.

Fabrizio Panaioli 2020