Il "peccato" di 10° è irrazionale.**
La prima volta che ho visto questo problema, a cui sinceramente non ho dato molta importanza, è stato su un sito in lingua inglese; tutti conoscono il traduttore automatico di google, che a volte parte appunto da solo e traduce in italiano. Ho pensato : ma cosa c'entra questo con la matematica? L'ho poi ritradotto in lingua inglese, ed ha assunto la la forma:
dimostrare che il sin 10° è irrazionale.
Questo per ridere un pò e farvi capire quanto bene funzioni tale traduttore. Un complimento invece al collegamento peraltro un pò confuso che fa evidentemente con qualche nostra preghiera, o almeno io l'ho inteso così. Ebbene, visto che ho notato che i frequentatori del circolo amano la trigonometria, propongo di risolvere tale problema. Non sono ammesse soluzioni che comportano ragionamenti sulle cifre decimali estratte da calcolatrici o tavole. Al solito, siamo con carta e matita su un isola deserta. La soluzione si basa su poche righe, con pochissimi calcoli.






25 commenti
Si può dare per scontato che sen45° è irrazionale?
Senza usare le tavole, si tratta pur sempre del lato di un quadrato la cui diagonale è unitaria.
Scusa non ho capito la domanda. Cosa c'entra il sin 45?
Ci sono valori di funzioni trigonometriche che sono facilmente deducibili senza tavole, ad esempio...
sen 45° è il lato del quadrato che ha diagonale unitaria
sen 60° è l'altezza di un triangolo rettangolo che ha lato unitario
Si tratta di valori irrazionali perché espressi con radicali di 2 , di 3 ...
Potrebbero essere il punto di partenza per applicare formule di moltiplicazioni di archi e arrivare alla conclusione richiesta.
Scusa ma ho scritto "triangolo rettangolo" invece che "equilatero"
Sì ma è appunto quello richiesto. Non so da dove nasca una possibile confusione o se mi son spiegato male.
Non può bastare questo ragionamento?
Nella ipotesi che sin 10° sia irrazionale, sen 20° = 2 sin 10° cos 10° sarà irrazionale.
Non so se sin 20° sia irrazionale ma, se lo fosse, allora sen 60° = 3 sin 20° - 4 sin3 20°
dovrà essere irrazionale. Infatti lo è.
non capisco cosa tu intenda; il fatto che sin10° sia irrazionale è una tesi da dimostrare, non un ipotesi. E quella che vedo non sembra nemmeno una dimostrazione per assurdo, che comincerebbe con "supponiamo che sin10 sia razionale.. "
Utilizzo la formula di triplicazione degli archi mettendo in relazione 10° e 30°
sin 30° = sin 3*10° = 3sin 10° - 4 sin3 10° ponendo sin 10° = x e sapendo sin 30° = 1/2 riscrivo
1/2 = 3 x - 4 x3 ossia: -8 x3 + 6x -1 = 0
cerco i valori di x che azzerano questo polinomio
possibili divisori di -1 : p= (D-1) = ( +- 1 )
possibili divisori di -8 : q = (D-8) = ( +- 1 ; +-2 ; +- 4; +- 8 )
p/q = ( +- 1 ; +- 1/2 ; +- 1/4 ; +- 1/8 ) sostituisco i valori nel polinomio e trovo quali di essi lo azzera
P(1) = -8 +6/1 -1 = not 0
P(1/2) = -1/8 + 6/2 -1 = not 0
P(1/4) = -1/64 + 6/4 -1 = not 0
P(1/8) =- 1/512 +6/8 -1 = not 0
Non esistono valori di x razionali che azzerino per questo polinomio, soddisfacendo l'equazione.
Ma x = sen 10° quindi sen 1o° non è razionale.
Sì, formula di triplicazione a parte, non so se tutti abbiano capito ben il discorso delle radici. Bisognerebbe spiegare bene di quali proprietà è conseguenza. Comunque è giusto
comunque se qualcuno ha un idea diversa si faccia pure avanti. Il quiz e ancora aperto
Chi desiderasse rivedere la dimostrazione della formula di triplicazione degli archi la trova all'interno di questo mio articolo dell'anno scorso. (Magari, già che, c'è si legge anche l'articolo), Ci sono dimostrazioni più eleganti di questa, ma utilizzano la notazione dei numeri complessi. Il vantaggio è che qui trovate insieme anche la dimostrazione della formula di duplicazione. Attenzione il testo si apre cliccando "somma-archi" sotto la riga in caratteri rossi.
http://www.infinitoteatrodelcosmo.it/2019/01/13/lasteroide-questa-specie-ellisse/
il problema non è tanto la formula di triplicazione, che penso che i nostri trigonometrici conoscano tutti. Ma come ti dicevo sopra, il discorso delle radici. Andrebbe chiarito un pò di più almeno cosa si usa.
Si potrebbe utilizzare la Formula di Taylor per calcolare il sen 10°:
10° = π/18 rad
f(x0 + Δx) = f(x0) + f’(x0)Δx + f"(x0) Δx2/2 + f"’ (x0)Δx3/3! + …..
ponendo x0 = 0 , Δx = π/18
sen (0 + π/18 ) = sen (0) + cos (0) π/18 + 1/2 sen (0) (π/18 )2 +1/3! cos (0)(π/18 )3 ....
sen (0 + π/18 ) = 0 + π/18 + 0 + 1/6 (π/18 )3 .....
come si vede sen(0 + π/18 )= sen π/18 è dato dalla somma algebrica di frazioni di π (irrazionale) e di frazioni di π elevate a potenza
C' è il teorema della radici razionali come dice Maurizio.
Un altro modo è (anche applicando DEMoivre) , considerare l'equazione
facendo l'ipoesi di razionalità di x = m/n con m e n interi non entrambi pari
sviluppando si ha
se n è pari ci sarebbero due numeri pari a sin e a destra, ma m deve essere dispari
equindi si ha una incongruenza.
se n è dispari il membro di sin è dispari, ma m deve essere pari e quindi il membro di destra deve essere pari , altra contraddizione. Da cui si deduce che non esistoni m ed n interi, quindi x è irrazionale.
Scusate mi son dimenticato di inserire il caso m dispari e n dispari.
Anche in questo caso avremmo un membro pari a sinistra e uno dispari a destra, altra incongruenza.
non mi sembrano male queste idee nuove.. Leandro parla di teorema delle radici riferendosi a quanto detto da Maurizio.Ma io fino adesso non ho visto un chiaro enunciato di tale teorema.. o mi è sfuggito qualcosa.
quello che dice Michele è una nuova idea, e di questo sono contento. Ma lo sviluppo in serie dà il numero dopo una somma infinita, non una somma esatta. Che ne sarà del limite di questa somma?
l'enunciato del teorema delle radici razionali dice che le soluzioni di una equazione polinomiale a coefficienti interi ha la forma di una frazione p/q , in cui p è un divisore del termine noto e q è un divisore del coefficiente della potenza più alta. Ma vuoi solo questo enunciato o anche la dimostrazione ?
no. Non serve dimostrazione. Ma è stato enunciato solo adesso.
per Michele:
Non so cosa succeda a quella serie, ossia al limite della somma quando tende ad infinito.
Fatto sta, che se come dicono Maurizio e Leandro, sin 10° è soluzione dell'equazione:
N.B.:
E io invece sarei contento, visto lo spirito del Circolo, che certe affermazioni non siano considerate di dominio pubblico. Io ho sempre cercato di dare una dimostrazione il più semplice possibile di quanto proposto (o prima o dopo), anche nei casi più ostici. Il teorema delle radici razionali DEVE essere spiegato per bene in modo che tutti CERCHINO di capire. Questo, ripeto ancora, non è un circolo elitario ed è fatto per spiegare a tanti e non per scambiarsi pensieri, idee, in un ambito molto ristretto. Ci sono molti blog di pura matematica, soprattutto in inglese, ma questo non è uno di quelli. E' nato per altri scopi e come tale rimarrà fino a che ci sarò io.
Mi spiace, ma cercate di adeguarvi. L'ho detto e ripetuto, chi scrive non lo fa per dimostrare quanto è bravo, ma per cercare di divulgare quelle poche conoscenze che ha acquisito nella sua esperienza più o meno professionale.
Come diceva Pirandello... così è (se vi pare)!
Mi tocca dire che hai ragione. Come sai io ho un carattere un po' troppo accomodante. Comunque l avrei messo nella soluzione.
Grazie.
Il teorema delle radici razionali...
dice che.... Ogni soluzione razionale di una equazione polinomiale a coefficienti interi ha la forma di una frazione p/q , in cui p è un divisore del termine noto e q è un divisore del coefficiente della potenza più alta.
Se qualcuno desidera una dimostrazione rigorosa del teorema non la chieda a me. Posso solo dare questa modesta spiegazione:
Supponiamo che p/q sia una radice del polinomio e aggiungiamo che p/q è ridotta ai minimi termini, ossia p e q sono primi tra loro.
Ora sostituiamo nel polinomio questa frazione p/q
da cui, moltiplicando per ,
,
Osserviamo che p divide i primi n termini, dunque deve dividere anche l'ultimo termine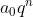
Dato che p e q sono primi tra loro ... allora p deve dividere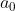 . (il termine noto)
. (il termine noto)
Analogamente si arriva a dire che q deve dividere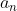 . ( il coefficiente del termine con potenza più alta)
. ( il coefficiente del termine con potenza più alta)
Mi auguro che sia sufficientemente chiaro per tutti.
Ringrazio te Umberto che hai capito cosa intendo. Devo anche dire che la spiegazione di Maurizio andrebbe data in un articolo a sé stante o, come hai detto tu, nella soluzione. Io farei un passetto in più e certe frasi sarebbe bene renderle più discorsive e comprensibili. Ad esempio:
...Osserviamo che p divide i primi n termini, dunque deve dividere anche l'ultimo termine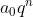 ...
...
Deve essere spiegata meglio, mettendosi in testa che molti lettori sono arrivati a questo punto con le basi dategli dalla matematica del corso che è in archivio. Lo sforzo maggiore nella divulgazione non è ripetere enunciati o dimostrazioni, ma di mettersi sempre dalla parte di chi legge e chiedersi: "Ho detto cose che tutti sanno o hanno i mezzi per potere capire?" Spesso questo non capita.
La cosa è soprattutto grave in un quiz con 2 asterischi. Buttare giù formule o teoremi che nessuno ha mai spiegato è cosa molto controproducente per il Circolo. Io accetto, e Umberto lo sa bene, molti dei suoi articoli, diretti a un livello piuttosto alto. Chi non si sente all'altezza può fare a meno di seguirli. Accetto molto meno che durante i commenti di un quiz con due asterischi si usi questo sistema da "saputelli". Anche il bravissimo Leandro, spesso e volentieri, mira solo a rispondere senza pensare a chi legge e se ciò che ha detto può essere compreso da chi si aspetta una certa difficoltà...
Nei commenti, ha scritto... di brutto e senza alcuna spiegazione:
Un altro modo è (anche applicando DEMoivre) , considerare l'equazione
Beh, no, non lo posso accettare. Che lui sappia come si ottiene quella equazione mi fa molto piacere, ma si è chiesto se i lettori la conoscono?Se ne è mai parlato? e se sì, dai subito il link... oppure cerca di renderti molto più comprensibile. I commenti NON sono solo una risposta a un quiz privato, ma fanno parte dell'insieme divulgativo del Circolo. L'ho già fatto presente più di una volta. D'ora in poi (e con grande dispiacere) se qualche risposta o commento non seguirà queste regole mi vedrò costretto a eliminarlo, scrivendo di riproporlo in modo consono al nostro spirito che è e rimane quello iniziale!
Come già detto vi sono molti blog, in inglese almeno, che trattano argomenti specifici di alta matematica e molti sono anche fatti bene...
Si, hai ragione. Forse però ho sbagliato io a mettere questo quiz; in realtà per risolverlo , basta sapere le formule di addizione, che si possono applicare ripetutamente. Forse quelle tutti le conoscono. Poi, non serve nemmeno il teorema delle radici, ma si può ragionare su quella particolare equazione supponendo che abbia una radice razionale. Quanto hai due asterischi, potevano essere anche tre, ma più che altro 2,5. Non lo so, anche questo è soggettivo. Ho visto però di sovente usare nei quiz , al di fuori di questo, risultati molto impegnativi in matematica. La storia è già successa.
Hai ragione anche tu sul numero degli asterischi... è molto soggettivo, sicuramente. Insomma, cerchiamo di fare del nostro meglio e di riflettere bene prima di dare per "ovvie" o "conosciute" certe operazioni... Questo vale per noi, ma anche per chi commenta, ovviamente!