Categorie: Matematica
Tags: ala sinistra Cagliari geometria Gigi Riva quiz specchio della porta
Scritto da: Vincenzo Zappalà
Commenti:12
E' difficile fare goal per Giggiriva! (NEW: con piccolo aiuto)*
Chi ha un po' di anni come me non può non ricordare Gigi Riva, detto Rombo di Tuono, capace di dare un contributo essenziale alla vittoria dello scudetto del Cagliari (squadra che non ha mai lasciato) nel 1969-70. Ala sinistra formidabile, era un vero flagello per le squadre avversarie e i suoi goal tantissimi anche da posizioni non proprio perfette. Eh sì... per un ala sinistra (o destra) è necessario conoscere un po' di trigonometria o -almeno- un po' di geometria.
Gigi Riva, un mito per chi amava il calcio e l'agonismo, ma soprattutto per le donne, che lo mangiavano con gli occhi per il suo fisico atletico. Io non ho mai amato troppo il calcio, ma ricordo che quell'anno andai a vedere il Cagliari giocare a Torino essendo diventato un tifoso del Cagliari, una squadra non blasonata ma capace di "bastonare" tutte le grandi e danarose squadre più celebri.
Il suo ruolo era quello di ala sinistra e il suo tiro implacabile. Vale la pena riflettere un poco sulla difficoltà di tirare e segnare per un giocatore costretto a correre (forte) a una certa distanza dall'area della porta avversaria.
Cominciamo semplificando di molto la situazione. Immaginiamo che la partita sia giocata in un piano e che non esista il portiere. In queste condizioni è intuitivo che il momento migliore per tirare -e cercare di segnare- dipenda dall'angolo sotto cui l'attaccante vede la porta avversaria. Istintivamente si potrebbe pensare che più si è vicini alla rete e più grande diventa l'angolo che permette di far goal. In realtà, questo è vero per tutta la fascia del campo che unisce le due porte opposte (zona azzurra di Fig. 1). L'angolo cresce sempre di più andando verso la rete avversaria. Un attaccante che riesca ad arrivare fino alla linea della porta avrebbe davanti a sé un angolo di 180° e sbagliare vorrebbe dire tirare ... "indietro".
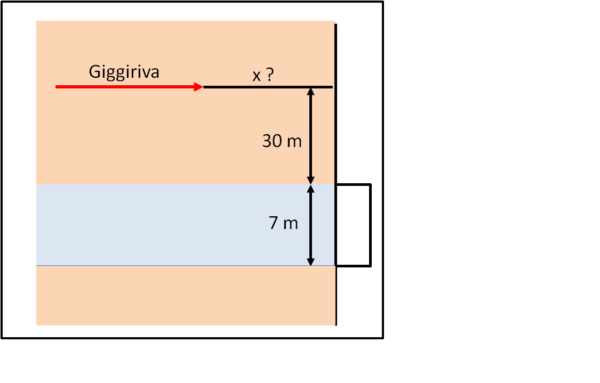
Un giocatore come Giggiriva (veniva anche chiamato così dai tifosi sardi) correva, però, all'esterno di questa fascia (nella parte rosa del campo) e per lui il momento di massima visibilità della porta avversaria era un piccolo problema di geometria o, se preferite, di trigonometria.
Vogliamo aiutarlo a trovare il momento giusto per la staffilata micidiale?
Sappiamo che una porta regolamentare è poco più di 7 metri di larghezza. Noi possiamo considerarla di 7 metri. Assumiamo anche che Giggiriva stia correndo a una distanza di 30 metri dalla linea immaginaria che congiunge i due pali delle porte, rivolti verso di lui. A che distanza dalla linea di fondo del campo avversario deve far partire il suo "sinistro" ? Si può risolvere sia con un minimo di trigonometria sia facendone anche a meno...
Se riceverò un po' di risposte dai "silenziosi" (i più bravi possono fare a meno di rispondere), potremo continuare e rendere sempre più realistica la situazione. In caso contrario lasceremo che il grande Riva segni a ... porta vuota!
PICCOLO AIUTO
QUI la soluzione
12 commenti
Ciao Enzo & C.a
Da anafabeta matematico di ritorno (la 5° liceo risale a 47 aa fa...e al "corso di matematica” sono solo alla 28° lezione...), avevo riflettuto sul fatto che l'angolo sotto il quale Riva vede la porta vada da 0 per X = infinito a 0 per X= 0, passando attraverso un massimo, che è quello che cerchiamo, credo.
denominando ß l'angolo sotteso dall'apertura della porta (7 m) che si trova a 30 metri dalla linea dove corre il giocatore, la funzione sarebbe:
ß=arctang(37/x)-arctang(30/x)
Di questa funzione dovrei individuare il massimo (ove la derivata è una retta parallela all’asse delle ascisse?)
Qui mi perdo (ammettendo di non essermi già perso prima...)
caro Franco,
grazie per aver affrontato il problema e non aver avuto paura di metterti allo scoperto. E così che si fa!!! Hai centrato il punto sicuramente... Ora, lasciamo perdere l'arcotangente e rimaniamo nelle tangenti. A te interessa, in pratica, l'angolo beta da esprimere in funzione di x. E allora prova a scrivere direttamente
tan(beta)
come tangente di un angolo che è la differenza di due angoli...
E a questo punto devo ammettere che la colpa è mia!! Abbiamo usato spesso le formule della somma dell'addizione e sottrazione degli archi, ma mi accorgo che nel corso di matematica non erano ancora state riportate. L'avevo preso per buono. BENE, grazie a te ora vedrò di correggere l'errore e fare un articolo dedicato a loro...
Per poterti fare andare avanti da solo fino alla fine del problemino ti riporto, per adesso, la formula della differenza per la tangente:
tan(a - b) = (tan(a) - tan(b))/(1 + tan(a) · tan(b))
Poi nell'articolo vedremo come ricavarla...
Comunque, vedrai che ti viene fuori una bella espressione in funzione della sola variabile x...
Poi continui come hai detto, sapendo che se la tangente raggiunge un massimo, lo raggiunge anche l'angolo...
Non voglio dirti niente di più, dato che puoi riuscirci benissimo da solo!
Chiedo scusa a te e a tutti gli altri
che hanno provato a risolvere il quiz, ma che si sono bloccati davanti alla differenza di tangenti. Ero sicuro di averne parlato, ma deve essere stato in un articolo a se stante che non trovo nemmeno io (magari Scherzy ce la farebbe... 
)
L'articolo generale arriverà quanto prima!!!
Ho usato tutti i potenti mezzi del blog e di Google, ma ghe nient da fa'... l'articolo sulla differenza di tangenti non l'ho trovato
Mi sa che non esiste, ti toccherà rimediare!
Sarà fatto!!
grazie a Scherzy e a Franco!! Però vi beccate anche le dimostrazioni...
Quindi:
tan(ß)= 7x/(x^2+1110)
derivata di un rapporto di funzioni, uguagliata a 0, risulterebbe massimo della funzione per x=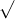
1110
?????
caro Franco,
dovresti scrivere meglio i passaggi che ti portano alla formula finale.. ricordando quanto valgono tan a e tan b...
e poi vedere cosa derivi... tan a e tan b li avevi già scritti... Comunque, se ti dei stufato non c'è niente di male... fai come preferisci...
caro Franco,
non vorrei essere stato male interpretato... Non ho detto che il risultato è sbagliato. Vorrei solo vedere tutti i passaggi, in modo che serva anche per gli altri lettori che non hanno osato intervenire..
Tra parentesi, il risultato è qualcosa di molto interessante, che ha un suo nome preciso...
Potresti chiamare h e d le due distanze e dare la formula finale in funzione delle due distanze, in modo da generalizzare il risultato.
Come dicevo nel testo, caro Franco... si può anche risolvere senza usare la trigonometria... Basta ricordare la proposizione 20 del III libro degli Elementi di Euclide (una cosa banale e molto usata) e il teorema di Pitagora...
Ti sto sfruttando per non scrivere la... risposta!
Ci provo, anche se mi incarto nello scrivere le formule. Euclide ! Che menti. Sono innamorato di Democrito..ma non divaghiamo.
Quindi: intendi "h" i 30 metri e "d" i 7 metri?
Chiamiamo allora α l'angolo che vede h (30) e β l'angolo che vede d (7)
Chiamiamo Α la somma di α+β (quindi l'angolo che vede h+d, = 37)
tan(β)=tan(A-α)=
Nel caso in esame:
tan(A)= (h+d)/x=37/x
tan(α)=h/x=30/x
quindi la 1) diventa:
tan(β)=((h+d)/x-h/x)/(1+(h+d)/x *h/d) con i nostri valori: (37/x-30/x)/(1+37/x*30/x)
tan(β)=((h+d-h)/x)/(1+(h+d)h)/x2)
tan(β)=(d/x)/(x2+ (h+d)h)/x2
tan(β)=d/x * x2/(x2+ (h+d)h)
tan(β)== dx/(x2+ (h+d)h)
con i nostri dati : tan(β)=7x/(x2+1110)
calcoliamo la derivata, è la derivata di un rapporto di funzioni , quindi:
y'= (d(x2+ (h+d)h)-dx(2x))/(x2+ (h+d)h)2
(d(x2+ (h+d)h)/(x2+ (h+d)h)2- 2dx2/(x2+ (h+d)h)2
Ponendo la tangente = 0 per determinare il massimo della funzione tang(β):
(d(x2+ (h+d)h)/(x2+ (h+d)h)2 = 2dx2/(x2+ (h+d)h)2
moltiplicando entrambi i membri per (x2+ (h+d)h)2
e semplificando
x2+(h+d)h=2x2
x2=(h+d)h
x=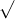
(h+d)h
Nel nostro caso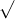
1110
Ora sotto con la matita rossa e blu
niente matita... caro Franco. Tutto bene!
Volevo solo far notare che scrivere √(ab) vuol dire scrivere la media geometrica tra a e b. Ne segue che la distanza dal fondo, da cui è meglio tirare, è la media geometrica tra le due distanze!!
Ma, se non vuoi fare calcoli di derivate e usare tangenti... c'è un modo più semplice per arrivare al... tiro! Euclide insegna
Prop. 20:
In un cerchio un angolo sul centro è doppio di uno sulla circonferenza, quando gli angoli abbiano come base lo stesso arco.
http://www.scienzaatscuola.it/euclide/home/libro3/prop3-20.htmlo
Che poi da questo si evinca quando deve tirare Riva....
Mo ci penso.
caro Franco...
ricorda che per tre punti passa una e una sola circonferenza...