Questo articolo è stato inserito nella sezione d'archivio "Sezione Aurea, spirale di Fibonacci e altre forme ricorrenti nell'Universo"

 

I numeri di Fibonacci e la sezione aurea sono concetti ricorrenti nell'armonia del Cosmo e anche nei capolavori concepiti dalla civiltà umana (specialmente nei suoi tempi migliori). Tuttavia, non smettono mai di stupire ed eccoli pronti a intervenire dove meno te l'aspetti.

In questo articolo, decisamente semplice, raccontiamo una delle solite "favole" o "fiabe" che siano, però, perfettamente realistiche nella loro "morale".

Attraverso la Relatività Generale abbiamo imparato a conoscere il mondo dei SEMPLI e dei COMPLI. I primi vivono senza chiedersi troppi "perché" e spesso si limitano ad accettare ciò che la Natura gli offre, traendone spesso conclusioni errate. Preferiscono, inoltre, credere ciecamente a chiunque si erga ad esperto o presunto tale. In tal modo fanno molta meno fatica a credersi sufficientemente "consapevoli".

I COMPLI  sono, a volte, molto noiosi, ma il loro linguaggio è la matematica, con la quale riescono a descrivere i fenomeni naturali. Spesso, purtroppo, si sentono portatori della verità assoluta e poco fanno per descriverla in modo semplice a chi non è al loro livello di consapevolezza (talvolta, però, fingono e non sono veramente così capaci)

I SEMPLI sono spesso faciloni e irritabili, dato che qualsiasi spiegazione appena appena troppo complicata li mette in imbarazzo. In qualche modo sono soprattutto "ignoranti" e, come frequentemente capita in questi casi, diventano arroganti quando gli si cerca di mettere in luce le imprecisioni e le conclusioni molto approssimative a cui giungono. I COMPLI sono pignoli e spesso rendono ancora più nervosi i SEMPLI, che non vorrebbero avere a che fare con dubbi e incertezze.

Due mondi che non riescono ad avere un vero linguaggio comune.

Un bel giorno un COMPLI si reca in visita nel mondo dei SEMPLI e, senza volere, ascolta un discorso senza capo né coda che viene declamato da un personaggio, circondato da un gruppo numeroso di ascoltatori, che sembrerebbe essere un uomo molto seguito e, soprattutto, deciso nelle sue affermazioni. Egli sta dicendo: "... E, quindi, vi ho dimostrato chiaramente che la "matematica" è priva di regole ben definite, roba da COMPLI, mentre la verità è ben altra. L'esempio che vi ho appena fatto è più che sufficiente a farvelo capire, dato che, come avete appena visto, 64 è perfettamente uguale a 65!"

Il COMPLI vorrebbe stare zitto, ma la corbelleria è più forte della sua pazienza, e interviene a gran voce: "Falso, se 65 fosse uguale a 64 sarebbe 65 e non 64. La matematica non è un'opinione di uno che parla senza conoscerla!".

Si accorge immediatamente di aver commesso una grave e pericolosa sciocchezza: il SEMPLI non è solo un loquace dispensatore di dubbie verità, ma è anche uno dei capi dell'intero mondo dei SEMPLI, un vera autorità, uno che può decidere tranquillamente il destino di chiunque gli si opponga. Infatti, senza nemmeno guardare negli occhi l'intruso, chiama a sé un gruppo di guardie armate  e gli ordina di tagliare u grosso telone in quattro forme geometriche: due trapezi e due triangoli perfettamente uguali tra loro, come mostrato in Fig.1.

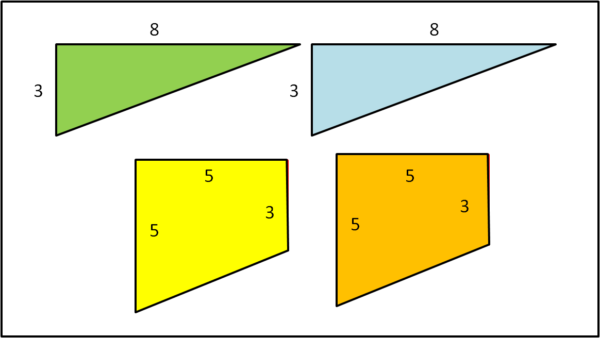
Poi ordina alle forze dell'ordine di trasportare le figure di tela, e il malcapitato COMPLI, su una grande piazza, dove aveva da poco svolto la sua esibizione.

Nella piazza (Fig. 2) sono disegnati per terra due poligoni molto semplici, uno è un quadrato di 8 metri per 8 metri e l'altro è un rettangolo di 5 metri per 13 metri.

Il SEMPLI fa disporre  i quattro teloni come mostra la Fig. 3 e copre l'intera figura disegnata per terra. Il che comporta che l'area  coperta perfettamente dai teloni sia di 64 metri quadrati (la moltiplicazione è qualcosa che sanno anche i SEMPLI...).

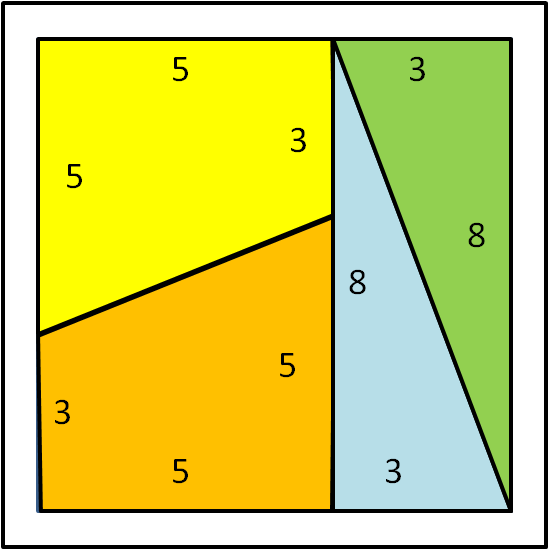
Poi comanda alle guardie di disporre i teloni sopra il rettangolo come mostra la Fig. 4.

Accidenti ... essi coprono nuovamente l'intera area. Con un ghigno malefico il SEMPLI esclama: "Caro COMPLI, con gli stessi identici teloni ho ricoperto esattamente sia un'area di 64 metri che una di 65, dato che 5 per 13 vale proprio 65! Hai visto che avevo ragione? Adesso sarai portato in galera per vilipendio delle regole base del nostro mondo, in attesa di un processo che ti condannerà a una pena severissima!". Poi continua: "E sappi che  che da noi esiste ancora la pena di morte per gravi offese alla nazione".

Il COMPLI ha solo un attimo di imbarazzo, ma poi mette in moto la  mente che trova immediatamente il baco nell'apparente "assurda" verità declamata dal SEMPLI.

N.B.: Volete risolvere voi l'apparente assurdità? Bene, fatelo prima di continuare a leggere!

Con un rapido scatto si porta sull'area rettangolare e invita il SEMPLI a guardare con attenzione cosa succede nel contatto tra le parti superiori e quelle inferiori: vi è uno piccolo, man ben visibile spazio vuoto. I teloni non coprono completamente l'area rettangolare! Il SEMPLI è costretto ad ammettere che è vero e rimane quasi impietrito, permettendo al COMPLI di spiegare brevemente la situazione, attraverso una geometria e matematica al livello dei SEMPLI.

Basta prendere la forma trapezoidale e tracciare la parallela all'altezza  e costruire un triangolo rettangolo. Il rapporto tra altezza (5) e differenza tra le due basi (2) quantifica la pendenza del lato diagonale (Fig. 5, a sinistra).

Tradotto in numeri:

2/5 = 0.400

Adesso basta fare la stessa cosa per il triangolo, che è già rettangolo, in modo da ricavare la pendenza dell'ipotenusa (Fig. 5, a destra). Essa risulta:

3/8 = 0.375

Lo stesso procedimento usato per meta del rettangolo (triangolo rettangolo di cateti 8 e 13 metri), porta a:

8/13 = 0.385

Il che dimostra che la diagonale del  rettangolo non coincide affatto con l'unione dei due lati diagonali dei teloni: questi ultimi cambiano pendenza e sono costretti a lasciare uno spazio vuoto. Non ci vuole molto a calcolare l'area di questo spazio vuoto, che altri non è che un parallelogramma molto sottile, come mostra la Fig. 6, in cui, per evidenziare grossolanamente la non coincidenza tra teloni e diagonale del rettangolo, non sono state mantenute le vere lunghezze.

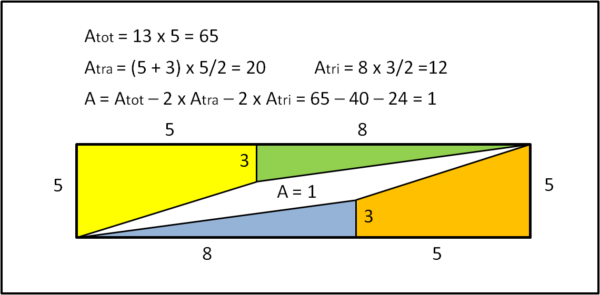
Tuttavia il conto è presto fatto...

Sia A_tot l'area del rettangolo, A_tra l'area del trapezio e A_tri l'area del triangolo. A è invece la differenza tra l'area del rettangolo e l'area dei due teloni, ossia l'area del sottile parallelogramma.

A_tot = 5 · 13 = 65 m²

A_tri = 8 · 3/2 = 12 m²

A_tra = (3 + 5) · 5/2 = 20 m²

A = A_tot - 2 A_tri - 2 A_tra = 65 - 24 - 40 = 65 - 64 = 1 m²

Dal pubblico che lo sta ascoltando scaturisce un "Ooooh" di meraviglia, mentre l'autorità e le guardie si dileguano in fretta e furia. Visto l'interesse sollevato, il COMPLI continua e dice: "Cari amici notate bene con che numeri abbiamo a che fare: 3, 5, 8, 13... A voi non dicono niente, ma nascondono un qualcosa di veramente universale, essenza stessa della natura e dell'armonia che voi amate tanto. Se volete ve li spiego in modo molto semplice e risulterà lampante quella differenza di un metro tra le due forme composte dai teloni che l'autorità SEMPLI voleva farvi credere fossero uguali. Mai fidarsi delle apparenze e usare sempre il cervello." I SEMPLI che sono aumentati di numero, rispondono all'unisono: "Siiiiii, spiegaci, spiegaci...!!!".

Il COMPLI inizia a spiegare la serie dei numeri di Fibonacci, dicendo che è facilissimo costruirla: dato il numero a e il successivo numero b, il numero seguente c è dato dalla somma di a e di  b. Quello ancora successivo, d, è dato dalla somma  di c e di b, e via dicendo

a

b

c = a + b

d = b + c

e = c + d

....

Nel nostro caso:

2        (a)

3        (b)

5 = 3 + 2      (c = a + b)

8 = 3 + 5      (d = b + c)

13 = 5 + 8     (e = c + d)

....

Poi, visto l'interesse, cerca di generalizzare il tutto, scrivendo le cose con più precisione e completezza:

"I numeri di Fibonacci sono:

F0 = 0

F1 = 1

F2 = 1

F3 = 2

F4 = 3

F5 = 5

F6 = 8

F7 = 13

...

e, come potete vedere facilmente, vale proprio quanto detto più rozzamente prima:

F2 = F0 + F1 = 0 + 1 = 1

F3 = F2 + F1 = 1 + 1 = 2

F4 = F3 +F2 = 2 + 1  = = 3

F5 = F4 + F3 = 3 + 2 = 5

F6 = F5 + F4 = 5 + 3 = 8

F7 = F6 + F5 = 8 + 5 = 13

...

L'autorità ha usato proprio  F5, F6 e F7

Nel nostro caso, però, va considerata un'altra proprietà dei numeri del signor Fibonacci: il quadrato di qualsiasi numero di Fibonacci è uguale al prodotto tra il numero precedente e quello successivo PIU' O MENO UNO. Ossia:

F_n-1 · F _n+1 = F_n² + (-1)ⁿ                      .... (1)

Volete la prova? Nel caso disegnato in piazza, abbiamo:

n = 6

Ossia:

F_n-1 = F₅ = 5

F_n+1 = F₇ = 13

Fn =F₆ = 8

Applicando la (1) abbiamo proprio:

5 · 13 = 8² +(-1)⁶ = 64 + 1 = 65

La stessa cosa succederebbe se considerassimo un quadrato di lato 5 e un rettangolo di lati 3 e 8. Avremmo  n = 5 e, quindi:

3 · 8 =  5 ² + (-1)⁵ = 25 - 1 = 24

Ma, ancora più semplicemente, guardate cosa succede se disegno un quadrato di lato 3 e un rettangolo di lati 2 e 5 (n = 4).

2 · 5 = 3² + (-1)⁴ = 9 + 1 = 10

Se il vostro SEMPLI avesse usato un quadrato e un rettangolo molto più grandi, la differenza sarebbe stata sempre di un  metro quadro e i teloni sarebbero sembrati sempre più perfetti anche per il rettangolo. Per dimensioni grandissime questa differenza tende veramente a zero, così come tende a un numero fisso il rapporto tra due numeri consecutivi di Fibonacci, il celebre rapporto aureo. Se poi ne voleste sapere di più vi invito a sfogliare il "bellissimo" blog L'Infinito Teatro del Cosmo e questa sezione, in particolare.

Mentre lui parla davanti a tante persone che sono rimaste a bocca aperta... sente qualcuno discutere ad alta voce: "Guardate! sto costruendo delle spirali, proprio come quelle che si vedono alla televisione sulle galassie, i cicloni, le lumache e moltissime altre cose... Ma allora la matematica è bella ed è seguita dalla Natura!".

I SEMPLI hanno imparato che, cercando di capire le cose e non solo accettandole per buone, ci si diverte un sacco e si diventa molto più riflessivi e critici verso chi cerca di ingannarci con prove del tutto false. In altre parole, si acquista consapevolezza di ciò che ci circonda, senza bisogno di portavoce.

Il COMPLI decide di andarsene in  silenzio, ma ha imparato anche lui una cosa: è molto più divertente cercare di spiegare le cose con semplicità piuttosto che discuterne soltanto con chi già le conosce. Anche lui ha acquistato consapevolezza del valore della semplicità, utilizzabile sempre quando si hanno le idee chiare.

E vissero tutti felici e contenti, mentre Fibonacci ridacchiava di nascosto...