Un quiz che ha ottenuto poco successo, ma che ha visto la risposta qualitativamente esatta di Daniela. Direi che vale la pena, comunque, di darne anche il risultato quantitativo.

Affrontiamo il problema con un minimo di metodo. La soluzione che per prima viene tentata è sicuramente quella di spostare le tovaglie mantenendo i loro lati paralleli. Per comodità e senza alterare la generalità del risultato, manteniamo quella gialla fissa e muoviamo le altre due. Il concetto di base è quello di cercare di aumentare in qualche modo il lato di quello considerato fisso. Il fatto stesso di voler ottenere un quadrato fa certamente pensare a una simmetria tra le posizioni delle due tovaglie vagabonde (blu e rossa).

La Fig. 1 ci mostra che sovrapporre i tre quadrati e poi spostare in direzione orizzontale o verticale  le due tovaglie libere di muoversi non porta assolutamente a nessun miglioramento. Si guadagna sia da un lato che dall'altro (come indicano le frecce), ma rimarrebbe sempre vuota la parte bianca indicata con il punto interrogativo. Niente da fare, la strategia è destinata a fallire.

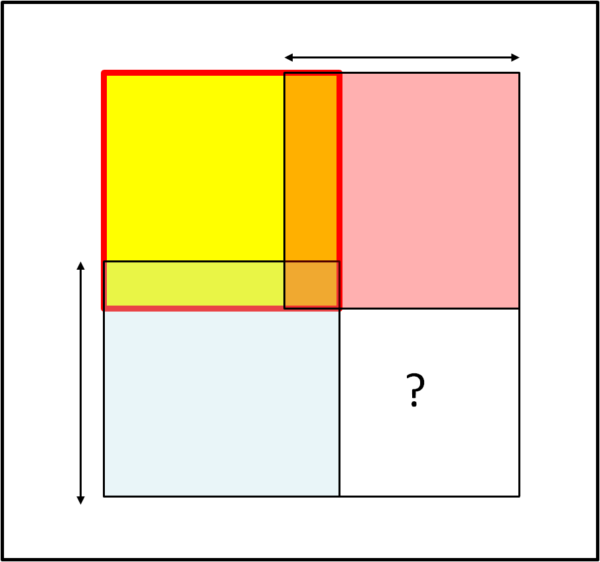
Analogo risultato avremmo spostando i quadrati "liberi" uno in verticale e l'altro in orizzontale. Le cose non cambiano assolutamente, dato che il quadrato che si riesce a coprire, senza lasciare spazi vuoti, è sempre quello di una singola tovaglia.

Non ci rimane che provare a ruotare le due tovaglie mobili. Per mantenere una simmetria molto ovvia basta ruotarli di 90°, come mostrato in Fig. 2.

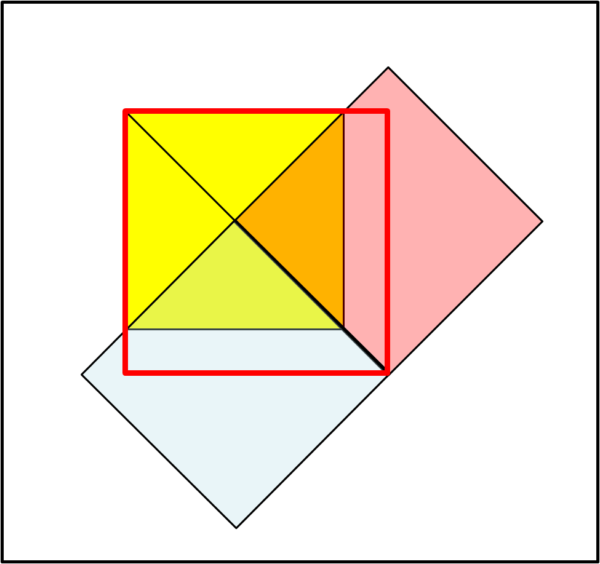
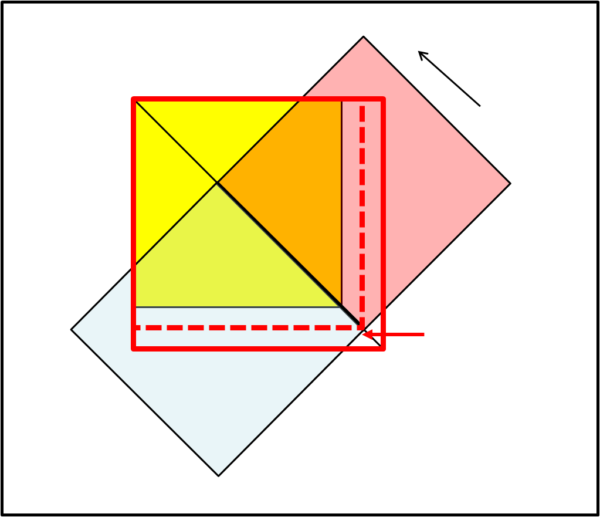
Accidenti... siamo riusciti nel nostro intento al primo colpo! Il quadrato che si può coprire, adesso, è decisamente maggiore di quello della singola tovaglia, come mostrato dal quadrato dal contorno rosso. Attenzione, però, che la manovra di rotazione e di sistemazione deve essere esattamente quella della figura. Se spostassimo i lati affiancati delle tovaglie rosse e blu verso l'alto (sempre lungo la diagonale della tovaglia gialla per ragioni di simmetria) nascerebbe uno spazio non coperto nella zona in basso a destra e il quadrato coperto diminuirebbe il proprio lato (perimetro tratteggiato) rispetto a quello precedente (Fig. 3a).

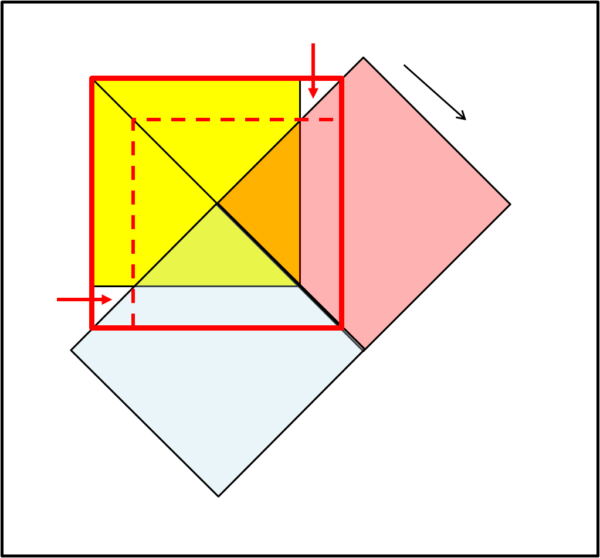
Risultato analogo se facessimo scorrere le due tovaglie verso il basso (Fig. 3b).

Va bene. qualcosa siamo riusciti a guadagnare. Non è nemmeno difficile calcolare la lunghezza del lato del quadrato dal contorno rosso, come mostra la Fig. 4.

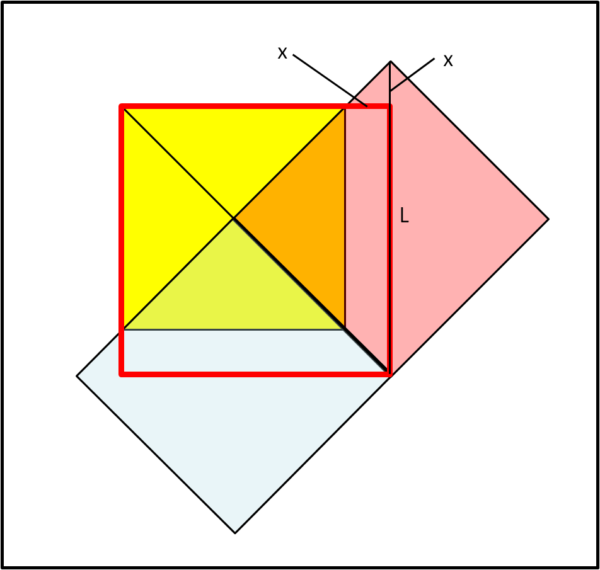
Chiamiamo x la parte in più del lato del nuovo tavolo rispetto a quello originario che è stato considerato unitario. Chiamiamo L la lunghezza del nuovo lato. Si ha subito che:

L = 1 + x

Ma anche che

L = √2 - x

Sommando le due relazioni sparisce x e otteniamo:

2L = 1 + √2

L = (1 + √2)/2 = 1.207...

Beh... un 20/% in più per il facoltoso e monumentale ospite.

Ma siamo sicuri che non si possa fare di meglio? Pensiamoci... e calcoliamo, se esiste, il nuovo valore di L.

Beh... Daniela (che con le tovaglie ci sa sicuramente fare) ha subito individuato una configurazione migliore, quella riportata in Fig. 5

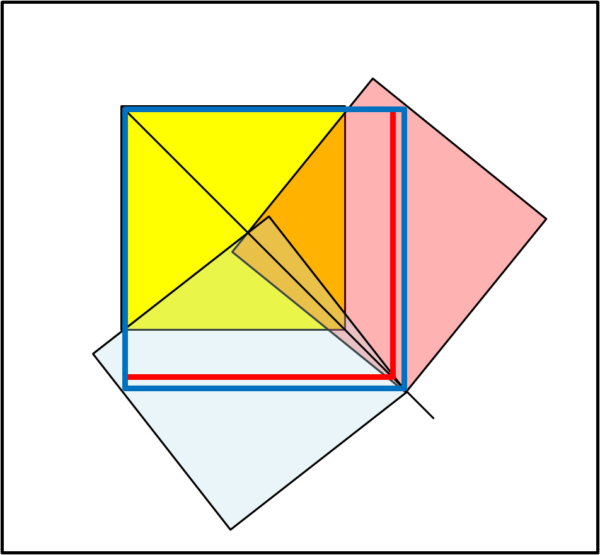
Riusciamo ad ottenere una superficie coperta quadrata delimitata dalla linea blu. Non molto, ma sempre meglio che niente. La configurazione deve essere però quella esatta, perché ruotando i due quadrati  (rosso e azzurro) di più o di meno spunterebbero subito delle zone "bianche", come mostra, ad esempio, la Fig. 6.

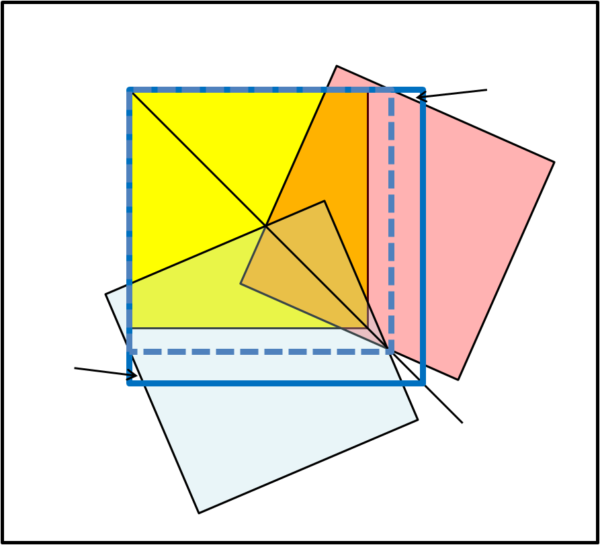
Non ci rimane che calcolare quantitativamente il nuovo valore di L e, per far ciò, usiamo la Fig. 7.

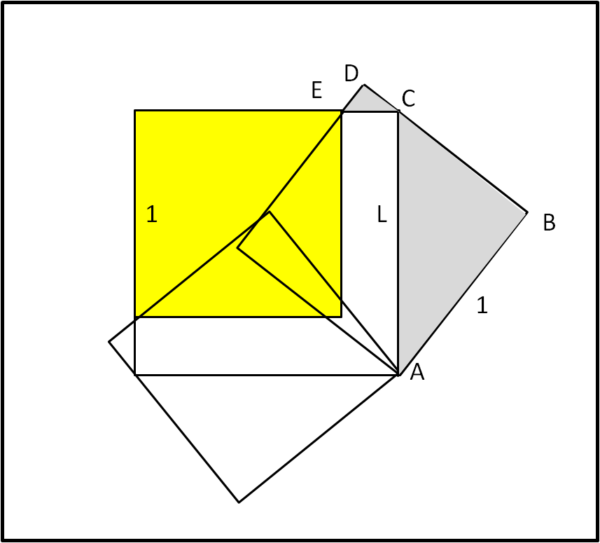
Consideriamo il triangolo rettangolo grigio ABC. Ovviamente AC = L e AB = 1. Attraverso Pitagora si calcola subito il cateto BC

BC = √(L² - 1)

Passiamo adesso al triangolo grigio più piccolo, CDE. Esso è simile al triangolo precedente e quindi possiamo scrivere la proporzionalità tra i lati. Sapendo che:

DC= 1 - √(L² - 1)

Possiamo scrivere:

AB/AC = DC/EC

1/L = (1 - √(L² - 1))/(L - 1)

- 1 =- L√(L² - 1)

1 = L²(L² - 1)

L⁴ - L²  - 1 = 0

Ponendo L² = x

x² - x - 1 = 0

x = 1/2 +/- √5/2

La soluzione accettabile è, ovviamente, quella col segno +.

Basta  scrivere:

L = √x

In cui si è preso nuovamente il segno + e si ha la soluzione:

L = √(1/2 + √5/2) = 1.272

Beh... il nostro "grassone" può finalmente sedersi!