Categorie: Matematica
Tags: esagono geometria quiz triangoli con la stessa area
Scritto da: Vincenzo Zappalà
Commenti:4
Un esagono particolare ***
In realtà questo quiz meriterebbe meno di tre asterischi, ma bisogna avere l'intuizione giusta e ricordare qualcosa che abbiamo imparato da poco.
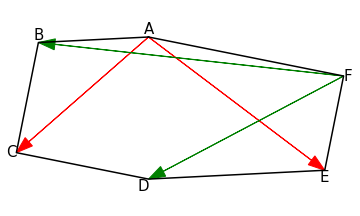
Consideriamo un esagono che abbia i lati a due a due paralleli (ma non uguali!). Sia esso ABCDEF, come nella figura che segue
Si chiede:
Dimostrare che i due triangoli ACE e BDF hanno la stessa area.
Non sono ammessi metodi analitici o trigonometrici.
N.B.: Per trovare la soluzione più rapida ed elegante dovete ricordarvi qualcosa che abbiamo presentato poco tempo fa e che ci ha aiutato ad ... allacciare le scarpe.
4 commenti
Ho letto l'articolo con il quiz e la relativa soluzione a cui fai riferimento in questo, caro Vincenzone. Tuttavia mi è venuto in mente questo metodo che, però, richiede un minimo di relazioni analitiche.
Con riferimento al triangolo marrone, riferito ad un sistema di assi cartesiani come in figura:
si ha immediatamente che
area triangolo marrone = area parallelogramma - area dei triangoli HDB, BGF e DEF cioè:
area marrone =y_{F}-\frac{1}{2}x_{E}(y_{A}-y_{F}))
che alla fine diventa
area marrone =)
Con riferimento al triangolo azzurro:
si ha immediatamente che
area triangolo azzurro = area parallelogramma - area dei triangoli HEC, EGA e ABC cioè:
area azzurra =(y_{A}-y_{C})-\frac{1}{2}(x_{B}+x_{E}-x_{A})y_{A})
che alla fine diventa
area azzurra =)
confrontando le espressioni area marrone area azzurra si nota che l'unica differenza è nei termini
ora, le espressioni (1) e (2) uguali. Infatti basta considerare i triangoli AGF e HDC. Essi sono simili, si dimostra immediatemente (hanno i tre angoli rispettivamente congruenti). Per cui, scrivendo la relazione di proporzionalità tra le basi e le rispettive altezze si trova proprio lpuguaglianza tra le espressioni (1) e (2). Quindi, le aree dei due triangoli marrone e azzurro sono uguali.
E lo so, il metodo è sicuramente fuori tema rispetto al suggerimento di applicare quanto scritto nel quiz del triangolo e le scarpe, ma stavolta mi è saltato in mente questo. Anche per scrivere che ogni tanti ci sono e seguo con molto picare questo bellissimo Circolo
che bello risentirti caro Arturo! Ma sì, sarà anche fuori tema, ma è sempre una bella soluzione!
Dall’articolo suggerito da Enzo prendo l’informazione che l’area di un triangolo può essere espressa come metà del modulo del prodotto vettoriale di due lati.
L’uguaglianza delle due aree equivale alla uguaglianza dei prodotti vettoriali che le rappresentano, nel nostro caso (facendo attenzione ai versi di rotazione di un lato sull’altro):
AC˄AE= FB˄FD (AC, AE ecc. sono vettori e ˄ è il simbolo del prodotto vettoriale)
che equivale a:
AC˄AE-FB˄FD=0
Questa è la relazione che cerco di dimostrare nei passaggi seguenti sviluppando il termine a sinistra.
Per fare questo sviluppo utilizzato alcune proprietà dei vettori e del prodotto vettoriale:
Seguendo in figura i percorsi tra gli estremi dei vettori, vedo che i quattro vettori possono essere espressi come:
1) AB+BC+CD+DE+EF+FA=0 poiché forma un percorso chiuso
2) il prodotto vettoriale di due vettori paralleli è nullo, es. AB˄ED=0
3) scambiando i fattori del prodotto vettoriale si inverte il segno, es. BA˄BC=-(BC˄BA). Non è commutativo.
4) due vettori uguali ma orientati in verso opposto danno somma nulla, es. AB+BA=0, vale a dire AB=-BA
5) per il prodotto vettoriale vale la proprietà distributiva, es. (AB+BC)˄AF=AB˄AF+BC˄AF
AC=AB+BC
AE=AF+FE
FB=FA+AB
FD=FE+ED
Sostituisco i vettori sopra con i loro equivalenti:
AC˄AE-FB˄FD=
(AB+BC)˄(AF+FE)-(FA+AB)˄(FE+ED)
espando i prodotti
AB˄AF+AB˄FE+BC˄AF+BC˄FE-FA˄FE-FA˄ED-AB˄FE-AB˄ED=
Poiché BC è parallelo a FE ed AB è parallelo ad ED, posso eliminare questi due prodotti vettoriali che sono nulli.
Posso eliminare anche i due termini +AB˄FE-AB˄FE, uguali e contrari.
Ottengo:
AB˄AF+BC˄AF-FA˄FE-FA˄ED
Noto che in tutti i termine appare AF o FA.
Per portarlo a fattor comune, cerco di portarlo al secondo termine del prodotto nella forma AF giocando sui segni.
Devo portarlo dalla stessa parte del prodotto vettoriale perché questa operazione non è commutativa.
-FA˄FE=AF˄FE=-FE˄AF=EF˄AF
-FA˄ED=AF˄ED=-ED˄AF=DE˄AF
Così posso portare a fattor comune AF:
AB˄AF+BC˄AF-FA˄FE-FA˄ED=AB˄AF+BC˄AF+EF˄AF+DE˄AF=
(AB+BC+EF+DE)˄AF
AB+BC+CD+DE+EF+FA=0 poiché forma un percorso chiuso,
allora AB+BC+DE+EF=-CD-FA, quindi:
(AB+BC+EF+DE)˄AF=-(CD+FA)˄AF
CD ed FA sono paralleli ad AF, quindi il loro prodotto vettoriale con AF è nullo
Così dimostro che la relazione AC˄AE-FD˄FB=-(CD+FA)˄AF=0 è valida e le aree dei triangoli ACE ed FBD sono uguali poiché i due prodotti vettoriali che le calcolano sono uguali.
come sempre molto interessante caro Fabry ... ma io pensavo a qualcosa di estremamente più semplice, tenendo conto solo dell'enunciato S(ABC) = S(PAB) + S(PBC) + S(PCA) ... più qualche triangolo con la stessa area...