Categorie: Matematica
Tags: abbassamneto di grado divisione Paolo Ruffini polinomio regola di Ruffini resto teorema di Ruffini
Scritto da: Vincenzo Zappalà
Commenti:5
Regola di Ruffini **
Questo articolo è inserito in Matematica e Geometria
La regola di Paolo Ruffini (1765 - 1822) viene facilmente (e ingiustamente) dimenticata. E' giunto il momento di rispolverarla.
Lo scopo di questa serie di operazioni ha lo scopo di abbassare il grado di un polinomio, una volta che è nota una sua radice. In altre parole, vogliamo trasformare un'equazione di grado superiore n al secondo nel prodotto di un polinomio di primo grado per un polinomio di grado n - 1.
Abbiamo un'equazione di grado n:
axn + bxn-1 + cn-2 + .... + d = 0
di cui vorremmo conoscere le "radici", ossia i valori di x che soddisfano l'equazione, ossia -ancora- che annullino il primo membro.
Affidiamoci al Teorema di Ruffini (su cui si basa la susseguente regola):
Un polinomio di grado n è divisibile perfettamente per un altro polinomio di primo grado se e solo se la radice del polinomio di primo grado soddisfa il polinomio di grado superiore.
In altre parole: se xo è una radice del polinomio di partenza, allora il "resto" della divisione DEVE essere zero e il polinomio di partenza può essere scomposto esattamente nel prodotto del polinomio di primo grado per un altro polinomio di grado n -1.
Ossia:
(x - x0)(a'xn-1 + b'xn- 2 + ... + c') = 0
In parole ancora diverse, dobbiamo riuscire ad abbassare il grado del nostro polinomio di grado n, dividendolo per l'equazione lineare (x - x0). Il che vuole dire trovare i nuovi coefficienti a', b', ..., c'.
Fondamentale è, a tal riguardo, la regola ideata dallo stesso Ruffini che ci permette di ottenerli con l'utilizzo di una semplice TABELLA.
Prima di mostrarla, però abbiamo bisogno di conoscere una radice del polinomio, in modo da determinare il polinomio di primo grado che è, perciò, della forma:
x - xo = 0
Questa ricerca si affida alla pazienza e all'occhio di chi deve eseguire la divisione. Normalmente si parte dai numeri più piccoli e si cerca di ragionare per esclusione.
Ammettiamo di averlo determinato e che quindi x0 sia una radice.
Disegniamo la Tabella 1:
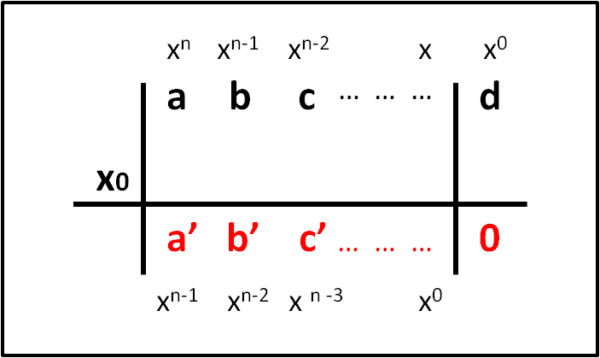
A sinistra, in basso, scriviamo la radice x0. Dentro le due righe verticali, in alto, scriviamo i coefficienti a, b, c, ... Al di là della seconda riga verticale scriviamo il termine noto d. Sopra di loro ho inserito, per non confonderci, la corrispondente potenza di x . Ovviamente, x0 = 1.
Tracciamo una linea orizzontale, in basso, dove compariranno i coefficienti a', b', c', ... del polinomio abbassato di grado (come indicano le potenze di x che ho aggiunto). Al di là della seconda riga verticale ho messo ZERO, dato che quella posizione corrisponde al RESTO, che nel nostro caso deve essere nullo. Se, dopo lo svolgimento delle operazioni non venisse ZERO significa che abbiamo commesso qualche errore di calcolo o che x0 NON era una radice.
Vediamo di calcolare i coefficienti scritti in rosso.
Il procedimento è molto semplice (attenzione ai segni!)
Abbassiamo direttamente a che diventa a'. Poi, moltiplichiamo questo a' (uguale ad a) per la radice x0 e inseriamo il risultato sotto la colonna del b. Lo sommiamo a b e il risultato diventa il nostro b'. Prendiamo questo b' e lo moltiplichiamo nuovamente per la radice. Il risultato lo inseriamo sotto a c e sommiamo, ottenendo c'. Continuiamo con questa operazione fono a terminare i coefficienti, ossia arrivando all'ultima moltiplicazione che sarà inserita sotto il termine noto d e che sommato a lui DEVE dare ZERO.
Il polinomio abbassato di grado dopo la divisione è quindi:
a'xn-1 + b'xn-2 + ... + c'
Facciamo subito un esempio numerico che ci permette di non usare simboli troppo lunghi e confusionari.
Il polinomio di partenza sia un polinomio di terzo grado:
x3 + 3x2 - 5x + 1
Troviamo una radice della corrispondente equazione:
x3 + 3x2 - 5x + 1 = 0
Proviamo con x0 = - 1
(- 1)3 + 3 · (-1)2 - 5 · (- 1)3 + 1 = -1 + 3 - 5 + 1 = 3 ≠ 0
No, non va bene...
Proviamo con x0 = 1
13 + 3 · (1)2 - 5 · (1)3 + 1 = 1 + 3 - 5 + 1 = 0
Perfetto! x0 = 1 è proprio una radice dell'equazione. Possiamo, allora scrivere la nostra Tabella 2.
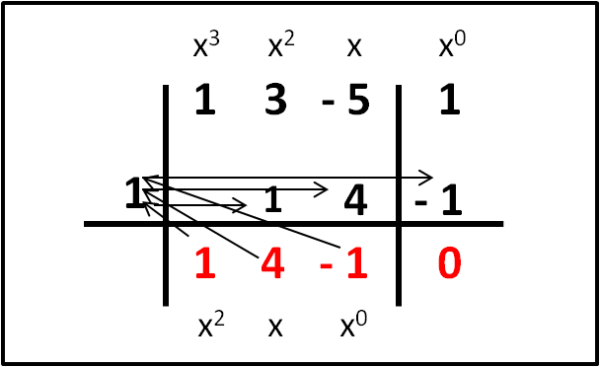
Abbassiamo il coefficiente di x3. Moltiplichiamolo per 1 (xo) e il risultato (1) lo inseriamo sotto il coefficiente 3 di x2. Facciamo la somma (4) e scriviamola in basso. Moltiplichiamo questa somma per 1 (xo), il risultato (4) lo inseriamo sotto il coefficiente - 5 di x. Facciamo la somma (-1) e scriviamola in basso. La prendiamo, la moltiplichiamo per 1 (x0) e la portiamo sotto il termine noto (1). La somma dà 0 come previsto.
Il polinomio di secondo grado che abbiamo ottenuto dividendo il polinomio di partenza per (x - 1) risulta essere:
x2 + 4x - 1
Possiamo perciò scrivere:
x3 + 3x2 - 5x + 1 = (x - 1)(x2 + 4x - 1)
L'equazione da risolvere è, quindi:
(x - 1)(x2 + 4x - 1) = 0
Una radice è, ovviamente, x0 = 1 , mentre le altre due si determinano trovando le soluzioni di una semplice equazione di secondo grado:
x2 + 4x - 1 = 0
x1,2 = - 2 +/-√(4 + 1) = -2 +/- √5
Bene, imparata la regola di Ruffini, teniamocela ben stretta perché ... potrebbe servirci quanto prima!






5 commenti
Molto utile questa regola veniva insegnata durante il biennio delle scuole superiori nel corso di algebra e dopo il capitolo della scomposizione dei polinomi in fattori ( dove "casca l'asino" come diceva la mia professoressa di matematica) ,
Spesso viene dimenticata ma serve sia come aiuto per la scomposizione dei polinomi in fattori, per lo studio delle disequazioni, per lo studio delle funzioni....ecc.
Bei tempi ... eravamo giovani
eh sì, caro Michele...
E' un piacere ritrovarla! Una cosa mi è sempre piaciuta dell'assistere i figli nei loro impegni scolastici: trovarsi a rispolverare regole e dimostrazioni imparate da studente e poi spesso rimaste inutilizzate. Ci si ricorda della loro esistenza, del nome che portano, della loro utilità ma i dettagli operativi....persi in un mare di altre dimenticanze. Poi, quando ti capitano davanti, le rispolveri e sembra quasi di ripercorrere i sentieri di un tempo e via via riconoscerne svolte e declivi....
Che nostalgia, mentre ti leggevo mi sono sfilati davanti i volti di tutti i miei insegnanti di matematica. Tutti morti, ovviamente.
In questi giorni sta circolando in rete un articolo su Huffpost di Alessandro Barbano intitolato "Se non si conosce l'analisi logica non si capiscono democrazia e pandemia. Solo nell'equilibrio tra esattezza e senso del limite si fonda la corretta tensione tra vaccini e libertà".
Voi direte: cosa c'entra ora l'analisi logica? C'entra, c'entra... È in questo delicato equilibrio che abbiamo avuto la grande fortuna di essere stati educati a partire dalle elementari "prima che la scuola e la cultura abbiano irresponsabilmente disdetto le basi della conoscenza sostituendolo con competenze e abilità".
https://www.huffingtonpost.it/entry/se-non-si-conosce-lanalisi-logica-non-si-capiscono-democrazia-e-pandemia_it_61c836cae4b0bcd2194b1338
Caro Albertone, c'entra... c'entra, eccome!
La scuola sta aiutando a far vincere l'incapacità logica e la voglia di scoprire. Ruffini è un esempio... va bene la regola, ma senza il teorema perde di senso. Va bene saper risolvere problemi già impostati, ma impostarli, e capire il perché, è la vera conoscenza!
Come ti capisco...