Abbiamo già parlato a lungo del paradosso della ruota di Aristotele (almeno così viene indicato), risolto in modo fantastico da Galileo attraverso un ragionamento che apre le porte al concetto di infinito. Quello era un paradosso essenzialmente fisico anche se sembrava coinvolgere la sola geometria. Di pura geometria si discute invece quando si descrive il paradosso della moneta, su cui avevamo proposto un paio di quiz (QUI e QUI) e che era stato descritto e risolto in vari modi, entrando nel regno di curve fantastiche come la cicloide, l'epicicloide, l'ipocicloide, e via dicendo e -perché no?- del moto della Luna e non solo.

Torniamo, oggi, su quest'ultimo paradosso e ne diamo una soluzione estremamente semplice e che evita formule di qualsiasi tipo. Una soluzione che ci permette di generalizzare completamente il paradosso di base e prevedere il risultato per tutti i casi che si vogliano.

Cominciamo con il semplice rotolamento di una moneta su un un tavolo piano. Ben, niente di più facile nel rispondere a una domanda altrettanto semplice: "Quanta strada percorre la moneta sul tavolo, dopo aver completato un giro attorno al proprio centro ?".

Prendiamo la nostra moneta rossa e segniamola con un punto bianco che stia, all'inizio del movimento nella parte più alta della moneta. Facciamola rotolare senza strisciare sul tavolo, fermandoci quando il punto raggiunga nuovamente la posizione di partenza.

Beh... penso che anche i bambini diano rapidamente una risposta: il tragitto della moneta sulla tavola è esattamente uguale alla lunghezza della circonferenza. Per convincersene immediatamente, basta, ad esempio, pensare a una moneta che abbia attorno alla sua circonferenza un nastro fissato al tavolo nel punto più basso (A). Mentre la moneta rotola il nastro si svolge e la moneta si ferma quando tutto il nastro è steso. La moneta ha ovviamente completato una rotazione attorno al proprio centro e il tragitto effettuato è pari alla lunghezza del nastro, ossia della sua circonferenza, come mostra la Fig. 1.

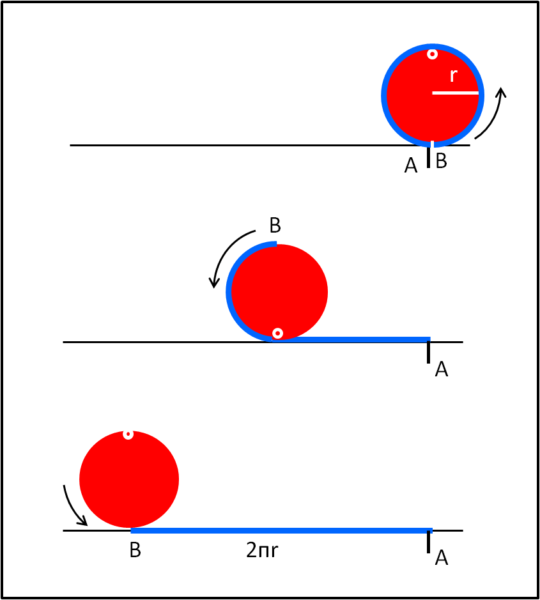
Bene, tralasciamo la... "cicloide" (il tragitto compiuto da punto bianco) e prendiamo come dato di fatto ciò che abbiamo osservato.

A questo punto, al posto del tavolo, prendiamo una moneta azzurra esattamente uguale alla moneta rossa. Poniamo la seconda sopra la prima, con il punto bianco nella parte alta. Ciò che vogliamo fare adesso è far rotolare esternamente, la moneta rossa attorno alla moneta azzurra, . Ci poniamo la domanda: "Quante rotazioni attorno al proprio centro deve fare la moneta rossa per rotolare attorno alla moneta azzurra e tornare nelle condizioni iniziali ?".

Una logica affrettata sembrerebbe darci la risposta velocemente: il percorso che la moneta rossa esegue attorno alla moneta azzurra è lungo esattamente come la circonferenza della moneta azzurra. Ma, la moneta azzurra è identica alla moneta rossa, per cui il percorso compiuto dalla moneta rossa deve anche essere pari alla propria circonferenza. Risulta apparentemente ovvio, ricordando la Fig. 1, che durante un rotolamento di lunghezza pari alla circonferenza la rotazione della moneta rossa debba essere una e una sola.

Vogliamo provare?

Consideriamo la Fig. 2 e facciamo rotolare la moneta rossa lungo la circonferenza della moneta blu, fermandoci in posizioni particolari del suo movimento.

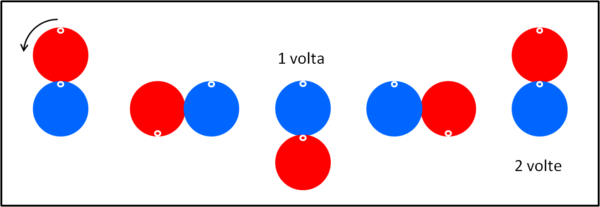
Accidenti, c'è qualcosa che non va... la moneta rossa durante il suo rotolamento lungo il bordo della moneta azzurra viene a trovarsi con il punto bianco nella sua parte alta non una sola volta, ma ben due volte. Il che implica che la moneta rossa ha eseguito due rotazioni attorno al proprio centro. Eppure, accidenti, ha compiuto un tragitto del tutto uguale, in lunghezza, a quello della Fig. 1.

Prima di andare a fondo della questione, complichiamoci ancora un po' la vita e facciamo un esperimento analogo, prendendo, però, la moneta rossa con un raggio pari alla metà di quello della moneta azzurra.  Nuovamente, sembrerebbe ovvia la risposta... la moneta rossa ha una circonferenza che è pari alla meta di quella azzurra. Se deve compiere un rotolamento completo attorno a lei è obbligata a percorrere un percorso che è doppio di quello che le è necessario per ruotare attorno al proprio centro (Fig. 1): la moneta rossa "deve" ruotare esattamente due volte attorno al proprio centro.

Non ci resta che provare e rappresentare il nostro tentativo nella Fig. 3, che richiama esattamente quanto fatto nella Fig. 2.

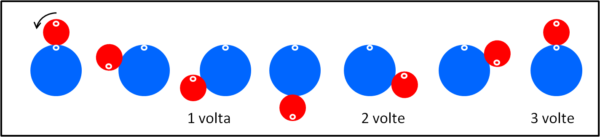
Ci eravamo illusi... Anche questa volta le nostre attese non sono state confermate dai fatti. La moneta rossa, infatti, per tornare nella condizione iniziale deve effettuare ben tre rotazioni attorno al proprio centro. Il mistero si infittisce!

Ma, il bello, deve ancora venire...

Questa volta, consideriamo le due monete del caso precedente, ma inseriamo la moneta rossa all'interno della moneta azzurra (non chiedetemi come farlo praticamente e consideratela come prova fattibile). Partiamo sempre dalla stessa posizione, ossia con il puntino bianco verso l'alto (in questo caso il puntino bianco della moneta rossa coincide con quello della pallina azzurra). Facciamo rotolare la moneta rossa verso sinistra fino a completare il rotolamento lungo il bordo interno della moneta azzurra. Cerchiamo di ragionare con un minimo di logica, tralasciando le apparenti assurdità già riscontrate nei casi precedenti. Il percorso che deve eseguire la moneta rossa è esattamente lo stesso del caso di Fig. 2. Poco importa se rotola esternamente o internamente, questo percorso è nuovamente uguale alla circonferenza della ruota azzurra. Accidenti e ancora accidenti... questa volta non possiamo sbagliarci e dobbiamo concludere che le rotazioni eseguite dalla moneta rossa attorno al suo centro non possono che essere tali e quali al caso precedente di Fig. 2: stesso percorso, stesse rotazioni!

Abbiamo quasi paura a provare (e ne abbiamo ben donde...), ma lo facciamo in Fig. 4.

No! impossibile... non solo il numero di rotazioni è diverso da prima, ma si riduce addirittura a una soltanto!

A questo punto vien voglia di mettersi le monete in tasca e non pensarci più... e, invece, è il momento di ragionare con calma, aiutati, magari, da qualche formuletta. Chi vuol fare questo, trova pane per i suoi denti in questo articolo.

Tuttavia, si può anche comprendere ciò che è sembrato assurdo, ragionando in modo più empirico, utilizzando un nastro avvolto attorno alla moneta azzurra.

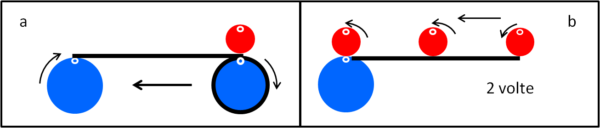
Cominciamo col caso delle due monete uguali e svolgiamo delle semplici operazioni (Fig. 5).

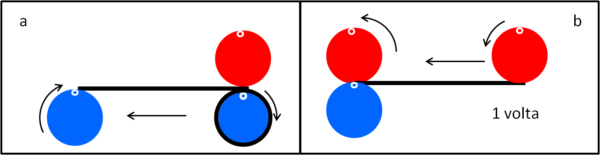
(a) Lasciamo ferma la moneta rossa e facciamo rotolare verso sinistra la moneta azzurra in modo che svolga completamente il nastro nero che la circonda. In questa operazione siamo sicuri che la moneta azzurra ha ruotato una sola volta attorno al proprio centro.

(b) Facciamo rotolare la moneta rossa in modo che vada a posizionarsi nuovamente sulla moneta azzurra, come all'inizio di tutto. Adesso sì che le cose sembrano essere perfette: la moneta rossa ha eseguito un percorso uguale alla srotolamento del nastro e ha ruotato una volta sola attorno al suo centro. Non ci rimane che concludere che avevamo sbagliato prima...

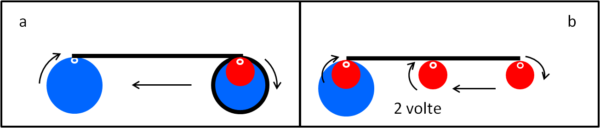
Ripetiamo le due operazioni anche con la moneta rossa pari alla metà di quella azzurra (Fig. 6)

Ma sì, tutto torna, adesso. Abbiamo ottenuto due sole rotazioni, come prevedibile. Avevamo di nuovo sbagliato. Sembra quasi di avere a che fare con il celebre esperimento della doppia fenditura di Feynman...

Non ci resta che provare, in Fig. 7, anche con il rotolamento interno e sperare ardentemente che le rotazioni siano solo due. D'altra parte cosa cambia girare sopra o sotto una linea che rimane sempre la stessa (la circonferenza della moneta azzurra)?

Tutto bene, ciò che finisce bene? Mica tanto... Le Fig.re 2, 3 e 4 sembravano proprio convincenti. Le operazioni (a) e (b) sono realmente sufficienti allo scopo? Un momento, un momento... abbiamo realmente raggiunto le condizioni iniziali? No, assolutamente no, dato che il nastro è tutto svolto. No, così non va, dato che nel rotolamento lungo la circonferenza il nastro non si svolge, ma resta dov'è. In altre parole, abbiamo fatto rotolare la moneta rossa su un piano, ma l'abbiamo anche fatta muovere di un tragitto pari alla circonferenza della moneta azzurra. Non ci resta che ripristinate le condizioni iniziali, lasciando ferma la moneta rossa che ha compiuto il suo lavoro. Ci resta un'ultima operazione da compiere per completare la Fig. 5: arrotolare nuovamente il nastro, tornando indietro verso destra, facendo rotolare la moneta azzurra, mantenendo, però, immobile la moneta rossa rispetto a quella azzurra (Fig. 5bis). In tal modo azzeriamo il forzato movimento della moneta azzurra.

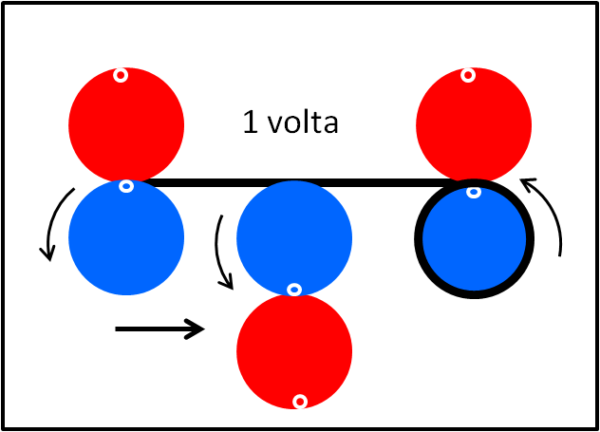
Adesso sì che possiamo contare le rotazioni della ruota rossa; una per raggiungere la ruota azzurra e una eseguita restando ferma e muovendosi solidalmente con quella azzurra: una più una uguale a due rotazioni.

Non ci resta che fare la stessa cosa, in Fig. 6bis, con la moneta rossa che ha un raggio pari alla metà di quella azzurra.

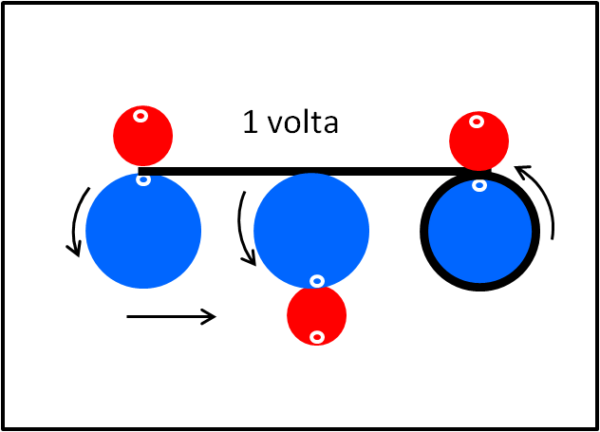
Ormai, sappiamo come fare: facciamo rotolare la moneta azzurra fino a riprendere la configurazione iniziale. In questo ultimo tragitto la moneta rossa è del tutto passiva, ma esegue una nuova rotazione attorno al suo centro. Conclusione: due più una uguale a tre rotazioni.

Tutto risolto? Nemmeno per sogno, accidenti... Svolgiamo la stessa operazione nel caso della moneta rossa che rotola internamente (Fig. 7bis).

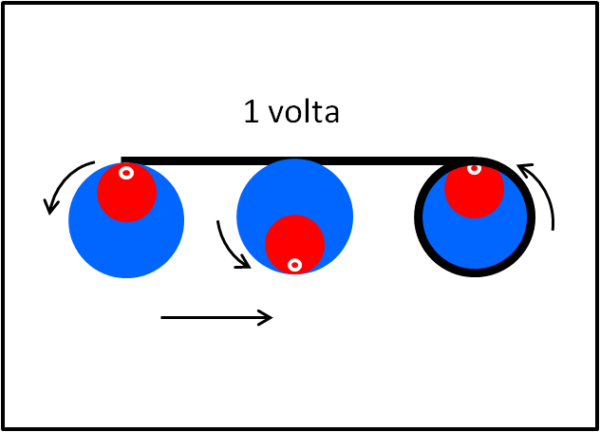
Tutto appare esattamente simile al caso precedente: due rotazioni della moneta rossa più una rotazione del sistema moneta azzurra-moneta rossa. Dovremmo trovare tre rotazioni... e, invece ne abbiamo osservato, direttamente, solo una. Dove l'inghippo? Presto detto: nell'ultimo caso il primo rotolamento della moneta rossa si effettua in senso ORARIO, mentre quello della moneta azzurra con la moneta rossa attaccata, si svolge in senso ANTIORARIO. Dobbiamo tener conto di questa inversione di verso e dare un segno negativo, per esempio, all'arrotolamento orario. Finalmente, le cose tornano:  due rotazioni orarie meno una rotazione antioraria è uguale a una sola rotazione oraria, proprio quella che avevamo osservato in Fig. 4.

Nei casi precedenti, le somme erano giustificate, dato che le rotazioni avvenivano tutte in senso antiorario e andavano sommate. Nell'ultimo caso, invece, il rotolamento della moneta rossa avviene in senso orario e quello di ritorno della moneta azzurra in senso antiorario.

Non abbiamo dato una vera dimostrazione geometrica o analitica che dir si voglia, ma abbiamo dato una spiegazione apparentemente empirica che ci permette, però, di risolvere, senza fare nessuna prova, qualsiasi altro caso con rapporti di raggio diversi tra le due monete, sia esternamente che internamente. Provare per credere...

Come già detto, per una dimostrazione più rigorosa basta andare a leggere questo articolo...