Una moneta che rotola... non solo un QUIZ. Seconda parte ***
Un piccolo corollario per chi non ne ha avuto abbastanza.... invece di avere due monete, abbiamo un anello e una moneta. La circonferenza dell'anello è tre volte quella della moneta.
Disponiamo l'anello sul piano verticale e ci mettiamo sopra la moneta (disco verde) la situazione è la medesima che conosciamo, la monetina verde, rotolando esternamente all'anello, farà quattro giri su se stessa e finirà per posizionarsi come alla partenza.
Adesso, leviamo la monetina blu e mettiamone una rossa, appesa (magneticamente) all'anello, come la vediamo nella figura.
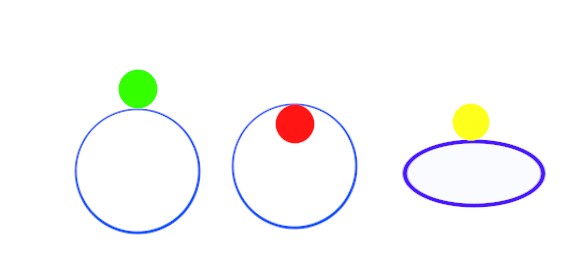
Ovviamente la domanda è : quanti giri compirà la moneta, rotolando all'interno dell'anello, prima di riposizionarsi come si trovava all'inizio?
Infine, tolta di mezzo la monetina rossa, sdraiamo l'anello sul piano orizzontale ( lo vedete come una ellisse) poi posiamo in verticale la monetina gialla. Ora è chiaro che la monetina nel fare il giro dell'anello, (come la ruota di un trenino sul binario circolare) farà una giravolta su se stessa, come una ballerina. Ma quanti giri completi avrà fatto questa volta ?
Adesso che avete tutte le risposte la domanda per la lode. se il piano della monetina non è coincidente né perpendicolare al piano su cui giace l'anello, cosa succede?
Volendo metterci la faccia (rigosamente da da schiaffi!), ecco la stessa figura di prima con le dovute aggiunte…
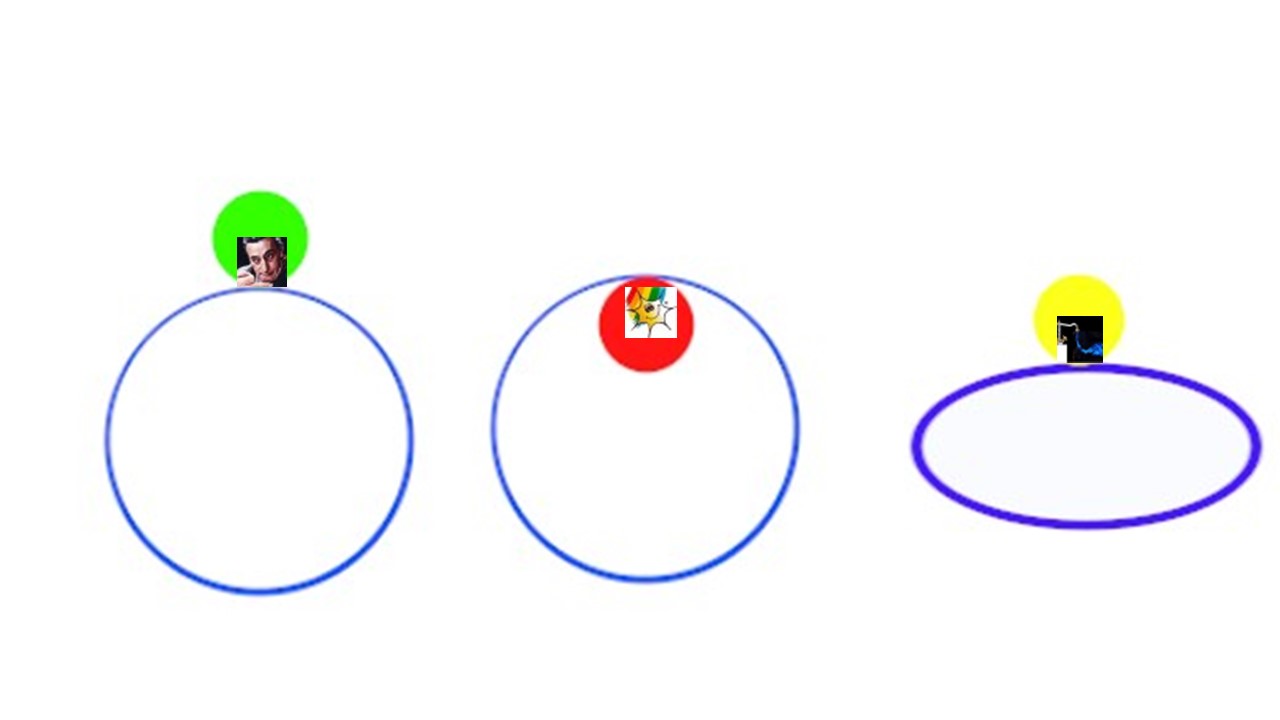
QUI la soluzione






26 commenti
1) Nel primo caso, rientriamo nell’ambito del quiz proposto, dove la distanza AB tra il centro del cerchio fisso B e il centro del cerchio rotante A è pari a 1 + 1/3 = 4/3 e il rapporto: (raggio fisso + raggio rotante) / (raggio rotante) = (4/3) / (1/3) = 4, sta ad indicare il numero di giri compiuti dal cerchio rotante prima di ritornare alla posizione iniziale;

regola generale:
(1 + 1/n) / (1/n) = [(n+1)/n]/(1/n) = n + 1,
con n = {raggio cerchio fisso} / {raggio cerchio rotante},
1 giro del cerchio rotante intorno al suo centro ogni 360° / (n+1) spazzati dalla distanza tra i 2 centri (raggio AB), con centro nel cerchio fisso (B):
360° / 4 = 90°
2) Nel secondo caso (cerchio rosso rotante all’interno del cerchio blu fisso), stesso rapporto raggio fisso / raggio rotante = 3, ma la distanza AB sarà pari a:
R(1 – 1/3) = (2/3)R;
rapporto (raggio fisso - raggio rotante) / (raggio rotante) = (2/3) / (1/3) = 2, che sta ad indicare il numero di giri compiuti dal cerchio rotante prima di ritornare alla posizione iniziale;
regola generale:
(1 - 1/n) / (1/n) = [(n-1)/n]/(1/n) = n – 1,
con n = {raggio cerchio fisso} / {raggio cerchio rotante},
1 giro del cerchio rotante intorno al suo centro ogni 360° / (n-1) spazzati dalla distanza tra i 2 centri (raggio AB), con centro nel cerchio fisso (B):
360° / 2 = 180°.
È interessante notare che in questa ipotesi, nel caso in cui cerchio rotante incluso e cerchio fisso includente abbiano lo stesso raggio, i due cerchi sono contemporaneamente “sovrapposti” e coincidenti, contemporaneamente uno fisso e se stesso in rotazione e l’ipotetica e irrazionale rotazione dell’uno con sé stesso avverrebbe ogni 360° / 0 = infinito spazzati dal raggio AB: la matematica ci dice col suo affascinante linguaggio che c’è qualcosa che non va.
3) Nell’ultimo caso, infine, si ha una sorta di movimento “cicloideo” di un cerchio che, anziché viaggiare su un binario retto, viaggia su un binario curvo a curvatura costante per tutti i suoi punti, e il numero di rotazioni del cerchio rotante per ritornare alla posizione iniziale è pari a:
2πR / [2πR(1/3)] = 3;
regola generale: 1 / (1/n) = n,
1 giro del cerchio rotante intorno al suo centro ogni 360° / n spazzati questa volta dalla proiezione della distanza AB sul piano dove giace la circonferenza di raggio R e centro in B:
360° / 3 = 120°.
Nulla cambia se il piano del cerchio rotante è diversamente incidente rispetto al piano del cerchio fisso: il cerchio di raggio (1/3)R e lunghezza 2πR(1/3) compirà sempre lo stesso percorso di lunghezza 2πR e come poc'anzi, la proiezione della distanza AB sul piano dove giace la circonferenza di raggio R e centro in B, spazza lo stesso angolo, come prima, per ogni rotazione del cerchio rotante intorno al proprio centro.
Io proporrei di mettere come "faccine da schiaffi", non autori e/o collaboratori e/o partecipanti al blog, tutte persone degne e rispettabili, ma le faccine di figure politiche sia italiane che internazionali, (tanto per non discriminare nessuno), che sul piano della dignità e rispettabilità magari hanno ben poco o niente da collocare.

Caro Andy, mi sembra che tu stia diventando una specie di Killer dei quiz...
Trovo particolarmente interessante la tua osservazione sulla moneta incastrata in un anello di pari circonferenza. Da un punto di vista fisico la sua rotazione rotolante è molto ambigua per quanto riguarda il punto di contatto, vuoi centro istantaneo di rotazione, perché i punti di contatto sono infiniti, sono contemporaneamente tutti i punti delle due circonferenze. Forse è questa la ricaduta sul piano della concretezza fisica, di quel risultato con cui la matematica ci lancia un avvertimento.
Mettere le faccine dei cattivi mi starebbe bene, ma come si fa poi, in pratica , a prenderli a schiaffi? Perché quella sarebbe, davvero, la grande soddisfazione...
Caro Oreste,
concordo con te, sarebbe una semplice soddisfazione "virtuale";
magari si potrebbe proporre una petizione per la non "sanzionabilità" dello schiaffo di monito morale al politico (solo uno, più di uno rientrerebbe nella "sanzionabilità" )
)
siete grandi, amici miei... scusate, ma io mi sto occupando del simbolo cinese Ying e Yang e di quella doppia "faccia da schiaffi" di Giapeto.... L'idea di Andy (un vero maestro...) è comunque mooooolto interessante, anche politicamente parlando!!!! Secondo me riuscirà a fregare Nobody prima di Pippo e Pappo nel prossimo quiz pappiano... (beccati questa Maurizio!!!!)
(beccati questa Maurizio!!!!)
Ecco il primo caso con una faccia da schiaffi tipica della nostra politica... Si vedono bene le 4 facce siderali e le tre sinodiche... (più una rovesciata... tanto per gradire...).
Con tutte queste facce da schiaffi da gestire dispiace di avere solo due mani....
Provo a inserire il grafico di Arturo anche qui... ma attenti con le mani!
https://ggbm.at/thw7ZKeN
Visto che abbiamo traslocato qui, riporto l'ultimo commento postato sulla prima parte...
Splendida dimostrazione che rende concretamente visibile tutto il meccanismo, Bravo Arturo !
Però, andando a rileggere il primissimo commento, ( nel quiz di partenza) ora che tutto è evidente a tutti, direi che anche nella affermazione di Oreste c'era una certa logica...
Ecco... brutto cattivo! Le mie faccine alla Pippo non ti sono piaciute eh?! Attento a te... che stanno per tornare!!!!
Oddio, Mi sento già male...
Piuttosto , che epicicli tiri fuori se ti blocco i centri delle due monete? Eccoti la figura...
Mi dichi... se i centri delle due ruote sono inchiodati, si osa dire che mentre quella grigia fa un giro quella gialla fa tre giri. E qui non ci pioviggina.
Ma gli epicicli... Gli epicicli delle facce da schiaffi , sono sempre gli stessi di prima? Io dico di sì, ma un povero disgraziato, uno che vede l'epiciclo già fatto... come fa a capire , se l'epiciclo è quello da fermo o quello con il giramento?
Aspettiamo, comunque, una bella animazione, con la solita faccia da schiaffi, anche della moneta interna...
mi era scappato...
scusa Oreste, ma se i centri sono bloccati ogni punto delle due circonferenze descrive solo e soltanto una circonferenza... non capisco...
Io non rotolo e nemmeno striscio per colpa di voi papalliani.
MLL Movimento liberazione della Luna.
Giusto, Leandro!
Diamo a Cesare... ops... alla Luna quel che è della Luna!!
Come si muove noi papalliani lo abbiamo spiegato qui
http://www.infinitoteatrodelcosmo.it/2017/02/11/i-racconti-di-ciccio-e-astericcio-appendice-alla-9-puntata-dalla-mela-alla-luna/
Giusta osservazione, Enzo. La domanda è questa:
Assumendo come sistema di riferimento quello solidale con la ruota grigia ( origine nel suo centro) il punto ( o puntacchio ) della ruota gialla che inizialmente è in contatto con la grigia descrive un epiciclo. Quanti giri ha fatto la ruota gialla al termine del primo epiciclo?
fammi capire meglio Pau...
il sistema di riferimento è solidale con la ruota grigia, ossia è un sistema rotante. Tu vuoi sapere come la rotazione della ruota gialla si vede considerando un sistema rotante di riferimento?
O sbaglio... mi sembra di essere tornato a Coriolis.....
Se è come dico io non dovrebbe cambiare niente. Basta considerare fisso il sistema rotante grigio e la ruota gialla non fa che rotolare attorno come prima... ma forse non ho capito...
Riguardo alla Luna sarebbe bello vedere come cambia il moto dell'epiciclo sul deferente cambiando la distanza Terra Luna rispetto al Sole posto sempre alla stessa distanza....
La Luna e la Terra si comportano proprio come i pianeti di Tolomeo... (La Terra sarebbe il centro dell'epiciclo e la Luna il pianeta che percorre l'epiciclo, considerando l'orbita terrestre come deferente).
Proprio così, il fatto che i due centri li vediamo fissi, perché siamo solidali con essi, non ci deve ingannare...non cambia nulla quando studiamo il loro moto relativo: il centro della ruota giallo, visto dalla ruota grigia, le ruota attorno.
E' chiaro che una vecchia volpe come te non si fa prendere in castagna...
Arturo, credo che ce l'abbia con te.... (spero)
Intanto che aspettiamo che Arturo torni dalla spiaggia....
https://www.youtube.com/watch?v=Ye8AxqndVYY
Perfetto Oreste! proprio quello che cercavo... Si vede molto bene come il moto retrogrado degli epicicli tolemaici si potrebbe trovare anche sulla Luna vista dal Sole se solo l'orbita lunare fosse più grande. Ci starebbe proprio bene un articoletto, così come uno per le soluzioni delle monete e (con calma) uno sulle curve varie dei rotolamenti. Vuoi occuparti di loro? O, almeno in parte... Vedo che sei molto ferrato!!!! Insieme ad Artù e magari Andy potreste mettere su un bell'articolo di casi vari con un po' di teoria (soluzione dei due quiz). Poi penseremo alle epicicloidi e cose del genere.... Io, intanto, sono arrivato quasi automaticamente al teorema di Copernico e vorrei parlare di quello...
Se fai il bravo, rimando il rientro di Pippo e Pappo...
Sì, bravo , parla di Copernico e lascia stare i Pappi, altrimenti finirà che mi devo fare operare di epicicloidi.
va bene, va bene, Ory (ti piace?), ma tu intanto organizzati con il geoArtù e con Andykiller per scrivere una bella risposta ai due quiz, con tanto di epicicli lunari....
Patti chiari e ... Pappi lunghi....
A mio modestissimo avviso, è anche interessante notare che, conoscendo misura del raggio del cerchio fisso R e frazione di "rivoluzione" in gradi (x°) della retta su cui giace il raggio vettore unente i due centri, necessaria al cerchio rotante per compiere 1 giro su se stesso, si può determinare la misura del raggio del cerchio rotante in funzione del raggio del cerchio fisso, secondo la relazione:
360° / (n+1) = x° ==> x°(n+1)=360° ==> n+1=360°/x° ==> n=360°/x° - 1
con n=(raggio cerchio fisso) / (raggio cerchio rotante).
Nell'esempio del quiz:
n=360/90 -1=3 ==> R=3r r=(1/3)R.
Ovviamente, invertendo i dati noti, ovvero conoscendo misura del raggio del cerchio rotante e frazione di rivoluzione del cerchio rotante intorno al cerchio fisso, si può determinare con la stessa relazione di prima, la misura del raggio del cerchio fisso.
Quello che comanda è la rotazione del raggio vettore che unisce i centri dei due cerchi.
In tutto questo ambaradan, abbiamo trascurato la velocità angolare del cerchio rotante (ma per la costruzione delle due figure nel quiz, questa è ininfluente ai fini della determinazione dei giri compiuti dal cerchio rotante intorno al cerchio fisso per ritornare alla posizione di partenza, sempre secondo la costruzione dei due cerchi come nel quiz).
Ma se cerchio di riferimento e cerchio orbitante ruotano entrambi, con la retta che unisce i due centri e che intercetta istante per istante non 3 punti (2 centri + 1 punto di contatto tra i cerchi), bensì 4 punti (2 centri + 1 punto sul cerchio di riferimento + 1 punto sul cerchio riferente), con velocità angolari differenti (addirittura anche con verso di rotazione opposto) le cose si complicano un pochino:
e qui interviene Enzo che ci straccia tutti
caro Andy,
mi sembra che sia tu che stia stracciando tutti! Cerchiamo, però, di non esagerare altrimenti ai poveri lettori le monete cominciano veramente a girare in testa come le rotelline del cervello... C'è abbastanza materiale per dare la risposta ai due quiz. Fate un buon lavoro, mi raccomando (sempre che tu sia disponibile a collaborare con quello screanzato di MauPau...). Io torno a Copernico....