Categorie: Matematica
Tags: Fibonacci funzione inversa quiz rapporto aureo Ruffini soluzione
Scritto da: Vincenzo Zappalà
Commenti:4
Soluzione del qualcosa in comune ****
Andy è stato bravissimo a risolvere il quiz. La "cosa in comune" non era altro che la soluzione delle due equazioni. Entrambe sono infatti soddisfatte dal celeberrimo rapporto aureo φ.
Cominciamo con la prima, ossia risolviamo l'equazione:
(x - 1/x)1/2 + (1 - 1/x)1/2 = x
Si potrebbe pensare di eseguire il quadrato di entrambi i membri...
(x - 1/x) + (1 - 1/x) + 2√((x - 1/x)( 1 - 1/x)) = x2
(x2 - 1 + x - 1)/x + 2√((x2 - 1)(x - 1))/x = x2
potremmo anche proseguire, ma dovremmo ancora eliminare una radice quadrata e il grado del polinomio salirebbe... No, non è la strada più comoda, si può dar di meglio, eseguendo un paio di sostituzioni "ad hoc". Torniamo alla nostra equazione di partenza.. e poniamo:
(x - 1/x)1/2 = u
(1 - 1/x)1/2 = v
da cui
u + v = x .... (1)
Moltiplichiamo, adesso, entrambi i membri per (u - v)
(u - v)(u + v) = x(u - v)
u2 - v2 = x(u - v)
Tuttavia sappiamo quanto valgono u e v e, di conseguenza, sappiamo anche quanto vale la differenza dei loro quadrati:
(x - 1/x) - (1 - 1/x) = (x2 - x)/x = x - 1
Da cui:
(x - 1) = x(u - v)
(x - 1)/x = u - v
Possiamo, allora, fare sistema tra questa e la (1):
x = u + v
(x - 1)/x = u - v
Sommiamo le due equazioni
x + (x - 1)/x = 2u
(x - 1/x) + 1 = 2u
u2 - 2u + 1 = 0
(u - 1)2 = 0
u = 1
Ma sappiamo che u vale anche (x - 1/x)1/2, per cui otteniamo:
(x - 1/x)1/2 = 1
quadrando
x - 1/x = 1
x2 - x - 1 = 0
Eh sì, è un'equazione che conosciamo bene e che porta come risultato proprio:
x = (1 + √5)/2 = φ
In realtà, avremmo anche un'altra soluzione
x = (1 - √5)/2 < 0
ma questa non è una soluzione accettabile per l'equazione di partenza. Infatti, il primo membro è la somma di due radici quadrate che DEVE essere sempre uguale a un numero positivo, mentre nel nostro caso avremmo che questa somma sarebbe uguale a una x negativa. L'unica soluzione reale è quindi quella che ci "regala" il rapporto aureo.
Ribadisco ancora che questa soluzione è stata trovata esattamente nello stesso modo dal nostro Andy. Bravo, veramente bravo!!
Passiamo alla seconda equazione...
2(2x + 1)1/3 = x3 - 1
Quanto detto da Andy è perfettamente corretto. Tuttavia, dato che abbiamo inserito anche la I vicino alla Q di "quiz" otteniamo la soluzione facendo uso di un concetto che penso non si sia mai trattato nel Circolo. Intendo parlare della funzione inversa.
Possiamo definirla in modo molto semplice: data una funzione f indichiamo con f-1 e la chiamiamo inversa quella funzione che ci permette di invertire la x con la y. In parole matematiche...
y = f(x)
x = f-1(y)
Un caso semplicissimo, ad esempio, è dato dalla funzione "elevamento a quadrato":
y = x2
la sua inversa esiste ed è, ovviamente, la funzione "estrazione della radice quadrata":
x = √y
Come fare a disegnarle su piano cartesiano? Beh... basta disegnare due funzioni che siano date dalle equazioni:
y = x2
y = √x
Ragioniamoci sopra un attimo: se avessi messo in grafico y = x2 e x = √y avrei disegnato due volte la stessa funzione. Scambiando x con y, invece, posso vedere come differiscono una certa funzione e la sua inversa. D'altra parte, poco conta quale variabile sia a sinistra o a destra, quello che conta è la funzione, ossia l'operazione che si deve svolgere su una certa variabile. Per poter confrontare realmente una funzione e la sua inversa è necessario scriverle entrambe come y = f(x) e y = f-1 (x).
Agendo in questo modo, ci accorgiamo subito che abbiamo introdotto una importante simmetria nel nostro grafico: avendo scambiato x con y risulta ovvio che gli unici punti che una funzione e la sua inversa possono avere in comune sono quelli per cui y = x, ossia quelli che stanno sulla retta y = x.
Ne segue che se ho una funzione e la sua inversa e voglio determinare gli eventuali punti in comune, è sufficiente che consideri una qualsiasi delle due funzioni e cerchi le sue intersezioni con la retta y = x.
Mostriamo la faccenda nel caso di y = x2 e y = √x. Le due funzioni sono una l'inversa dell'altra. Cerchiamone i punti in comune, ossia, risolviamo il sistema
y = x2
y = √x
Otteniamo subito l'equazione:
x2 = √x
Ma avremmo ottenuto lo stesso risultato facendo sistema tra una delle due funzioni, a piacere, e y = x
y = x2
y = x
da cui:
x2 = x
x (x - 1) = 0
Oppure
x = √x
x2 = x
x (x - 1) = 0
Riassumendo: se ci troviamo davanti un 'equazione che implica l'uguaglianza tra una funzione e la sua inversa non è necessario scrivere l'equazione risolvente, ma basta scrivere l'uguaglianza tra una delle due funzioni e la retta y = x.
Analizziamo, allora, la nostra equazione:
2(2x + 1)1/3 = x3 - 1
Scriviamola così:
(2x + 1)1/3 = (x3 - 1)/2
Poniamo
y = (2x + 1)1/3
vediamo se esiste la sua funzione inversa (basta esplicitare x in funzione di y)
y3 = 2x + 1
2x = y3 - 1
x = (y3 - 1)/2
Accidenti, Il secondo membro della nostra equazione è proprio la funzione inversa! In altre parole, la nostra equazione non è altro che l'uguaglianza tra una funzione e la sua inversa. Sappiamo allora che è inutile risolvere lei, dato che troviamo le stesse soluzioni uguagliando una delle due funzioni con y = x.
Facciamo allora sistema tra y = x e il secondo membro, ossia y = (x3 - 1)/2
y = x
y = (x3 - 1)/2
da cui un'equazione decisamente più semplice che ci assicura, per come è stata costruita, le stesse radici dell'equazione di partenza.
x = (x3 - 1)/2
x3 - 2x - 1 = 0
La simmetria ovvia tra una funzione e la sua inversa la vediamo anche graficamente inserendo la figura preparata da Andy per il nostro caso particolare:
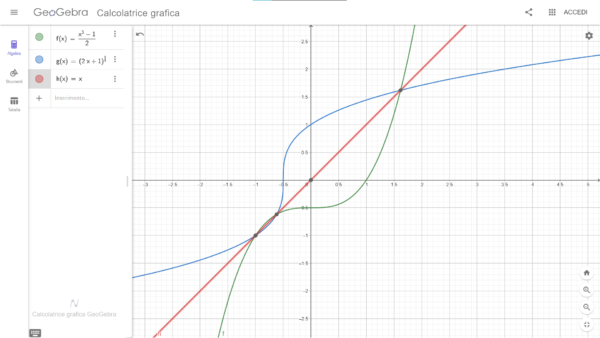
A questo punto si prosegue come fatto da Andy, ossia cercando una radice "semplice" del polinomio di grado 3.
x = - 1 fa proprio al nostro caso, per cui possiamo dividere il polinomio di terzo grado per il polinomio di primo grado (x + 1). Per far ciò basta ricordarsi la regola di Ruffini che abbiamo spiegato da poco...
Dividendo (x3 - 2x - 1) per (x + 1), Ruffini ci permette di trovare il polinomio di secondo grado che, moltiplicato per quello di primo grado, corrisponde esattamente al polinomio di terzo grado di partenza. Ossia:
(x + 1)(x2 -x - 1) = x3 - 2x - 1
Uguagliamo a zero il prodotto
(x - 1)(x2 -x - 1) = 0
dove, a parte la soluzione x = - 1, ci troviamo assolutamente come nel caso della prima equazione e il rapporto aureo è proprio la soluzione in comune.
Ancora un bravo ad Andy, che ho deciso di insignire del titolo di Primo Matematico del Circolo
Il quiz lo trovate QUI






4 commenti
Caro Enzo, sono onorato dei tuoi apprezzamenti, ma ritengo che nel Circolo ci sono Persone ben più preparate di me. La mia è una semplice passione per le Scienze Matematiche, ma grazie a Te e al Circolo, la mia "scintilla matematica" viene spesso accesa
Ti ringrazio Andy,
ma quando dico che sei veramente bravo sono sincero, credimi... E poi, cosa fondamentale, riesci sempre a far volare la fantasia, rendendo la matematica una scienza che tutto è meno che monotona e ripetitiva!
A presto Gran Primo Matematico!
Errata corrige:
Tuttavia sappiamo quanto valgono u e v e, di conseguenza, sappiamo anche quanto vale la SOMMA dei loro quadrati
Tuttavia sappiamo quanto valgono u e v e, di conseguenza, sappiamo anche quanto vale la DIFFERENZA dei loro quadrati
grazie Marco!