Bravissimo Andy che è arrivato alla soluzione. Io cercherò di arrivarci in modo diverso, più "lungo", ma forse più comprensibile.

Prima di passare all'azione, dobbiamo ricordare due importanti concetti legati alla trigonometria:

(1) Dato un punto P qualsiasi nel piano (x,y), di coordinate (a,b), determinare le coordinate (a’, b’) di P’, ottenuto ruotando P attorno ad O di un angolo ϑ

Disegniamo la Fig. 1 e ricordiamo due importanti relazioni trigonometriche (*):

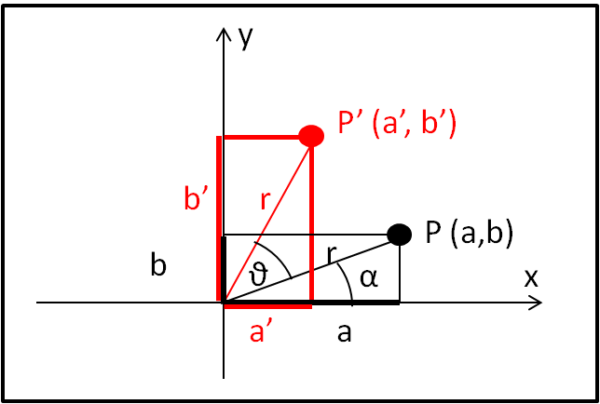
cos (α + ϑ) = cos(α) cos(ϑ) - sin(α) sin(ϑ)

sin (α + ϑ) = sin(α) cos(ϑ) + cos(α) cos(ϑ)

Applichiamole nel nostro caso

a’ = r cos(α + ϑ) = r cos α cos ϑ – r sin α sin ϑ = a cos ϑ – b sin ϑ

b’ = r sin(α + ϑ) = r cos α sin ϑ – r sin α cos ϑ = a sin ϑ + b cos ϑ

a' = a cos ϑ – b sin ϑ            .... (1)

b' = a sin ϑ + b cos ϑ

(2) Data una qualsiasi figura piana di Area A, se essa viene ruotata di un angolo f, la sua proiezione sul piano di partenza è sempre uguale a:

Ap = A cos f                          .... (2)

Proviamolo facilmente per il quadrato, ma vale per qualsiasi forma (Fig. 2).

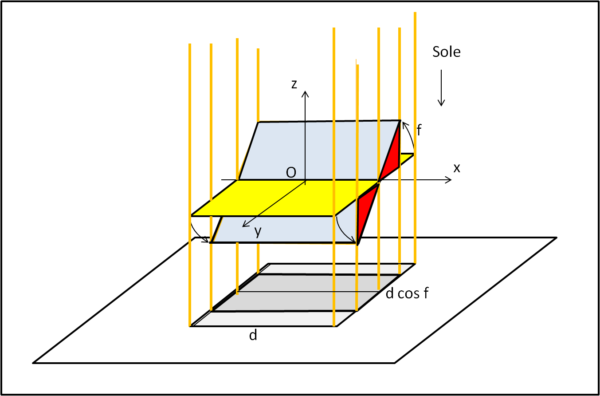
Il quadrato di lato d (giallo) è posto su un piano parallelo a quello di proiezione. L'asse z indica, infatti, la direzione del Sole. L'ombra grigio chiara è tale e quale al quadrato di partenza, la cui area è A = d².

Ruotiamo il quadrato attorno all'asse x di un angolo f, ottenendo il quadrato azzurro. Proiettiamo la sua ombra. Il lato parallelo all'asse x si conserva, mentre il lato parallelo all'asse y si contrare e vale d cos f. La nuova ombra (grigio scuro) vista dall'alto diventa un rettangolo di lati d e d cos f, la cui area vale proprio:

Ap = d d cos f = d²cos f = A cos f

Notiamo che pari risultato si sarebbe ottenuto ruotando il quadrato attorno all'asse y. Questo già ci dice che, data la simmetria della forma, per ottenere una configurazione qualsiasi del cubo, bastano due sole rotazioni.

Facciamo tesoro di quanto enunciato e dimostrato e passiamo al calcolo dell'area del cubo

Mi rendo conto che non è facile visualizzare correttamente un solido nello spazio a 3 dimensioni, per cui cerco di usare, per quanto possibile, proiezioni bidimensionali.

Consideriamo il nostro cubo messo in una posizione favorevole rispetto ai tre assi, ossia con l'asse z perpendicolare alla faccia superiore del cubo.  Ovviamente, in queste condizioni, l'ombra su un piano parallelo al piano (x,y) è cosa banale ed è proprio uguale all'area del quadrato di base. Andiamo per gradi e iniziamo con la prima rotazione, quella attorno all'asse z. Disegniamo, allora, il cubo visto dall'asse z (Fig. 3).

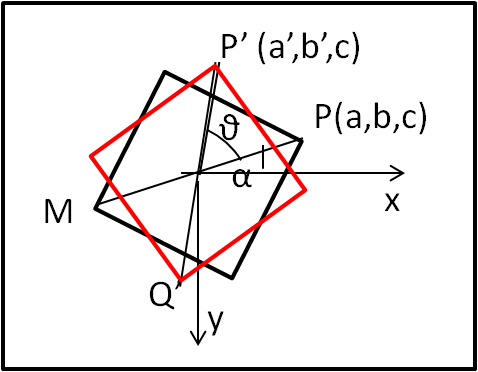
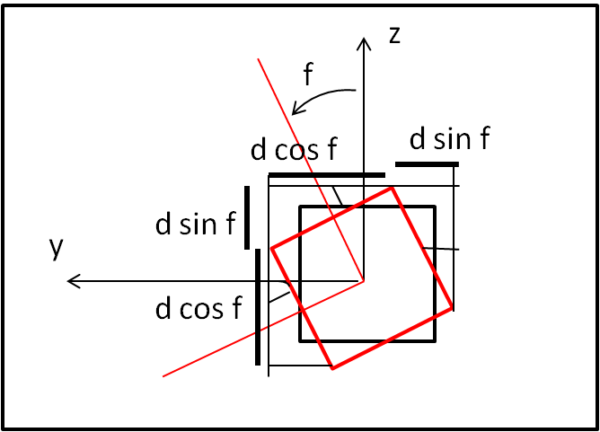
Risulta ovviamente un quadrato, qualsiasi sia la sua posizione sul piano (x,y). Per una trattazione generale, preferiamo pensare che il vertice del cubo P, nelle condizioni di partenza, sia ruotato di un certo angolo α iniziale rispetto all'asse x. In tal modo siamo pronti ad applicare la formula (1), ossia ricavare le coordinate a' e b' del punto P' a partire dalle coordinate a e b del punto P.

Possiamo scrivere:

a' = a cos ϑ – b sin ϑ         

b' = a sin ϑ + b cos ϑ

c' = c

abbiamo inserito anche la coordinata rispetto all'asse z che, ovviamente, rimane costante durante la rotazione.

A questo punto disegniamo la Fig. 4, ossia la proiezione del cubo visto dall'asse x, ossia nel piano (y,z).

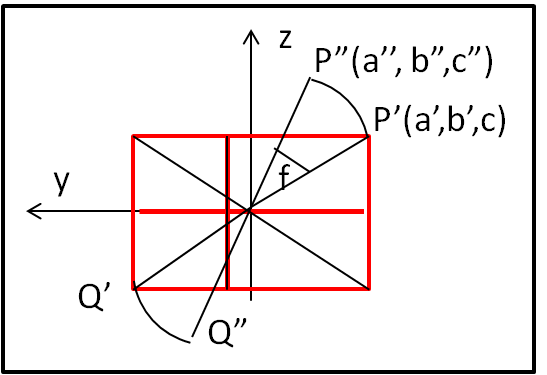
La proiezione del cubo è diventata un rettangolo, dato che la lunghezza della proiezione lungo l'asse y è maggiore di quella lungo l'asse z. Ciò che dobbiamo fare è ruotare il tutto attorno all'asse x di un angolo f. La situazione è tale e quale a quella che avevamo nel piano(x,y) dove però, le coordinate di partenza sono adesso a', b', c'= c.

In particolare, la nuova coordinata b', si comporta come la a nel caso precedente, mentre la c' si comporta come la b. In questa rotazione, ovviamente si conserva la coordinata a', dato che la rotazione avviene attorno a x. Possiamo scrivere nuovamente la (1) seguendo le piccole variazioni da apportare e determinare le coordinate del punto P":

a" = a'

b” = b’ cos f – c' sin f

c" = b’ sin f + c’ cos f

Non ci resta che sostituire a', b' e c' con i valori ottenuti precedentemente:

a” = a cos ϑ – b sin ϑ

b” = (a sin ϑ + b cos ϑ )cos f – c sin f

c” = (a sin ϑ + b cos ϑ) sin f + c cos f

Bene, abbiamo ottenuto ciò che volevamo nel modo più generale possibile. Ci possiamo, adesso, permettere di semplificare la faccenda e scegliere la posizione iniziale del cubo. Beh... come già suggerito  poniamo il suo centro nell'origine degli assi e i suoi lati paralleli ad essi. Le coordinate iniziali del punto P  diventano tutte uguali a d/2, così come quelle del punto Q diventano tutte - d/2.

Il punto essenziale che vogliamo raggiungere è scrivere la componente verticale della distanza tra P" e Q" ( h). Ciò vuole anche dire che ci basta considerare la componente z due punti finali P" e Q".

In altre parole:

la z del punto P" vale:

c"_P  = ((d/2) sin ϑ + (d/2) cos ϑ) sin f + (d/2)cos f

c"_P  = d/2 ( sin ϑ sin f + cos ϑ sin f + cos f)

Data la perfetta simmetria, il punto Q"  ha una coordinata z pari a:

c"_Q = - d/2( sin ϑ sin f + cos ϑ sin f + cos f)

Ne segue per ottenere h basta fare la differenza delle due relazioni, ossia:

h = c"P - c"Q = d(sin ϑ sin f + cos ϑ sin f + cos f))                   .... (3)

Lasciamo un attimo da parte questa fondamentale relazione e vediamo di applicare il secondo concetto. Esso ci serve per calcolare l'area dell'ombra sul piano (x,y).

Prendiamo il nostro cubo e indichiamo i vertici con delle lettere in modo da rendere più semplice la visione delle proiezioni e aggiungiamo anche i colori nelle facce del cubo (Fig. 5)

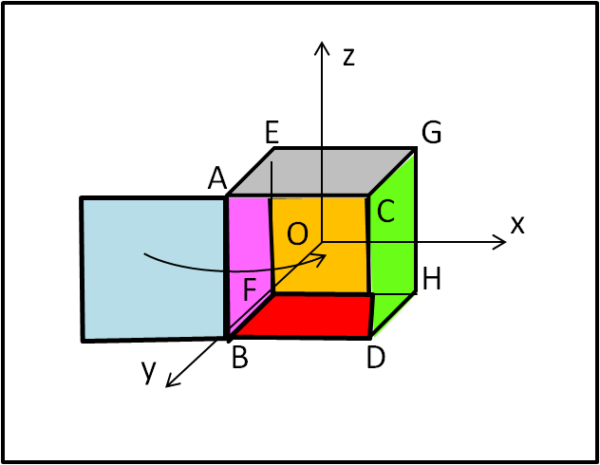
Disegniamo adesso la Fig. 6, dove in alto vediamo il cubo nel piano (x.y), ossia dall'alto, mentre in basso lo vediamo nel piano (x,z), ossia di lato. Per maggiore chiarezza usiamo segmenti colorati quando le facce si vedono "di taglio".

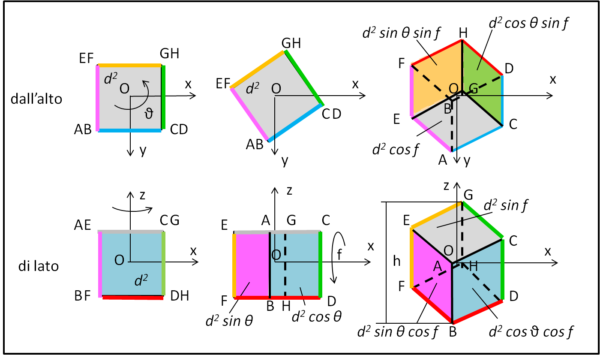
Una rotazione del cubo di un angolo θ attorno a z, non comporta nessun cambiamento nell'area vista dall'alto, che vale sempre d², mentre le facce laterali ruotate di un angolo teta danno luogo a due aree che valgono d² sin θ e d² cos θ, seguendo il risultato del secondo concetto (ricordando, ovviamente, che cos (90 - θ) = sin θ).

Le due facce così individuate NON si vedono nel piano (x,y), dove lasciano soltanto un segmento rettilineo che indichiamo nel cubo visto dall'alto.

Non ci resta adesso che ruotare il nostro cubo attorno all'asse x di un angolo pari a f . In basso abbiamo la proiezione vista di lato, ma a noi interessa quella vista dall'alto che è rappresentata nella parte superiore della figura. Per una migliore comprensione di ciò che si visualizza, usiamo anche la Fig. 7, dove il nostro cubo è visto nel piano (y,z). Una rotazione attorno ad x mostra molto bene le relazioni tra le facce del cubo viste lungo l'asse y (visione laterale) e lungo l'asse z (visione dall'alto).

Cosa concludiamo dalla Fig. 6?  Moltissimo! In particolare possiamo scrivere l'area vista dall'alto, sommando le aree delle tre aree visibili:

A_P = d²sin ϑ sin f + d²cos ϑ sin f + d²cos f

A_p = d(d sin ϑ sin f + d cos ϑ sin f + d cos f)

Ma la quantità dentro parentesi non è altro che la h data dalla (3). Ne consegue che:

A_p = d h

In poche parole, per qualsiasi configurazione del cubo, la sua ombra sul piano (x,y) è data dall'altezza h, ossia dalla differenza tra le "z" dei due vertici diagonalmente opposti P e Q.

Per semplicità, poniamo il lato d uguale a 1, in modo che l'area risulti uguale proprio all'altezza h.

Non è difficile, a questo punto, determinare l'area massima della proiezione sul piano (x,y).

Ruotiamo pure il cubo di 45° attorno all'asse z (massima lunghezza se visto dall'asse x o y, pari a √2) e poi ruotiamolo attorno all'asse x da 0 a 90°. Possiamo vedere i due casi limite, tridimensionale, nella Fig. 8, con le proiezioni (giallo e rosa) sui piani (y,z) e (x,y).

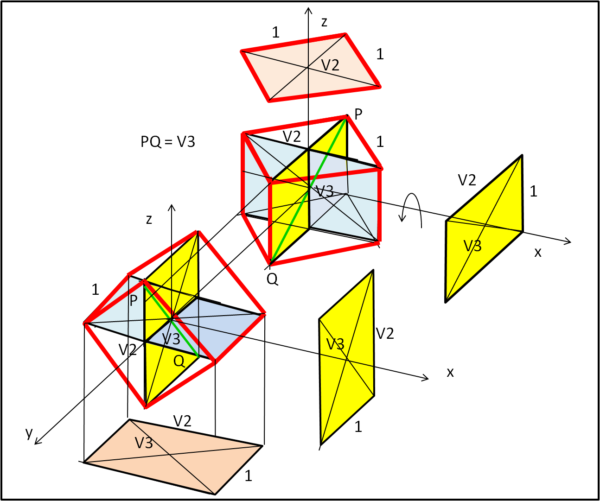
Tornando nei piani (x,y) e (y,z) rappresentiamo alcune configurazioni della proiezione gialla e della corrispondente proiezione rosa, in Fig. 9.

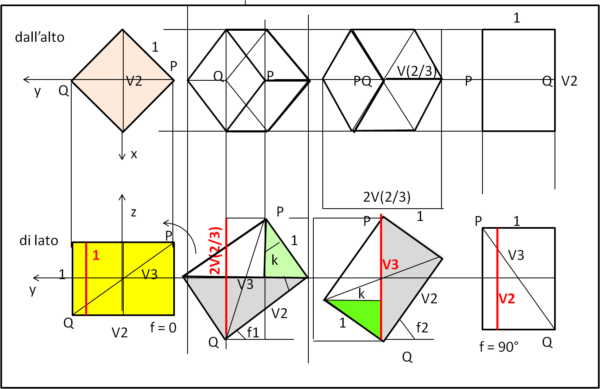
A sinistra abbiamo un rettangolo di lati 1 e √2 nella visione laterale, in cui la differenza di z tra P e Q vale proprio 1. Nella visione dall'alto abbiamo, infatti, un quadrato di area 1. Nella seconda configurazione abbiamo il solito rettangolo ruotato nella visione laterale, ma i due triangoli grigio e verde ci regalano il valore della differenza di z tra P e Q. Infatti, i due triangoli sono ovviamente simili e possiamo scrivere:

k : 1 = √2 : √3

da cui:

k = √2/√3

Ne segue che l'altezza h vale:

h =  2k = 2√2/√3

che è anche l'area dell'esagono nella visione dall'alto.

Continuiamo a ruotare e fermiamoci sulla configurazione più interessante: quella in cui la differenza di zeta tra P e Q è proprio uguale a √3. Questa è la configurazione con la massima altezza h e quindi con la massima area nella visione d'alto. Quest'ultima è un esagono regolare che ha il centro nei punti P e Q che si sovrappongono esattamente. La massima area della proiezione del nostro cubo vale quindi √3. I due triangoli grigio e verde sono ovviamente simili e k  ci regala il lato dell'esagono:

k = √2/√3.

L'ultima configurazione porta a una visione dall'alto di un rettangolo con l'altezza h che risulta essere  √2.

Per ottenere una visione diversa dello stesso risultato, possiamo considerare la formula trigonometrica che ci ha descritto h:

h = sin ϑ sin f + cos ϑ sin f + cos f

Poniamo θ = 45° , ossia

cos θ = sin θ = √2/2

h = √2/2 sin f + √2/2 sin f + cos f

h = √2 sinf + cos f

Per avere tutti i valori dell'area proiettata basta mettere in grafico questa funzione, con h (area) come asse y e f come asse x (Fig. 10)

Si ritrovano, ovviamente, i valori delle configurazioni di Fig. 9 con il massimo proprio uguale a √3.

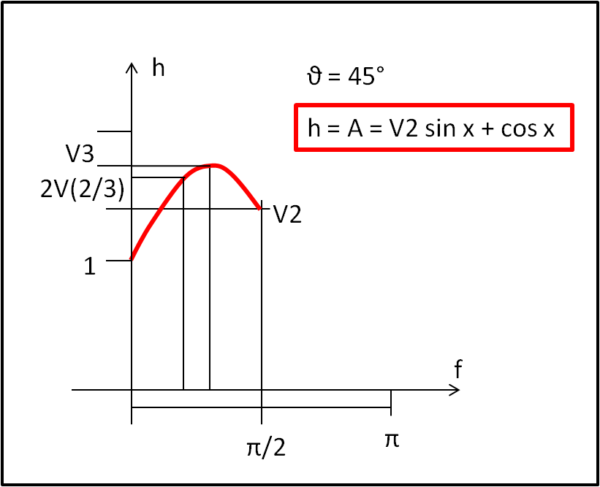
Si ritrovano, ovviamente, i valori delle configurazioni di Fig. 9 con il massimo proprio uguale a √3.

Per completare l'opera non ci resta che determinare gli angoli f1 e f2, attraverso la Fig. 9.

√2 sin f1 = √2/√3

sin f1 = 1/√3 = √3/3

f1 = 35.26° ...

√2 cos f2 = √2/√3

cos f2 = 1/√3 = √3/3

f2 = 54.74°...

Beh... una discreta fatica per avere a che fare con un cubo... Figuriamoci con un poliedro molto più complicato!

(*) Le ho sicuramente dimostrate da qualche parte, ma non ricordo più dove... nessun problema, possiamo sempre ricavarle di nuovo!

Il quiz lo trovate QUI