Categorie: Riflessioni
Tags: età logica quadrati perfetti quiz
Scritto da: Vincenzo Zappalà
Commenti:9
(Q) che età hanno le due amiche? **/***
Anna ha AB anni
Bruna ha CD anni
A, B, C e D sono singoli numeri interi di una sola cifra.
N.B.: AB non è il prodotto di A per B, ma un numero di due cifre, la prima delle quali è A e la seconda è B.
Il numero di 4 cifre (ABCD) è un quadrato perfetto
Tra 11 anni
Anna avrà EF anni
Bruna avrà GH anni
Il numero di 4 cifre (EFGH, che NON è il prodotto di EF per GH) è ancora un quadrato perfetto.
Che età hanno oggi Anna e Bruna?
QUI la soluzione
9 commenti
Mi manca un pezzetto... ma intanto:
siano x la radice quadrata di ABCD e y la radice quadrata di EFGH.
La differenza dei quadrati di y e x è 1111, cioè:
(y+x)(y-x)=1111
Ora vedo che 1111=91+93+95+97+99+101+103+105+107+109+111, somma di 11 numeri dispari.
Un quadrato differisce dal prossimo per un numero dispari, quindi segue che il quadrato di y è undici volte 'dopo' il quadrato di x, in altre parole:
y-x=11 [ECCO il pezzetto che mi manca, credo che questo lo si possa dimostrare assai meglio che così]
Mettendo insieme le due relazioni tra x ed y si ottiene x=45 e y=56, quindi attualmente Anna ha 20 anni e Bruna 25.
Mamma mia che velocità Francesco! Non dico ancora niente sulla bontà della soluzione...
Caro Enzo il mio ragionamento è questo:
Se ABCD è un numero intero di 4 cifre, allora deve essere
√1000 =< √ABCD =< √9999 ovvero:
32 =< √ABCD =< 99 (31 è da escludere perché 31^2 = 961 < 1000)
Tra 11 anni una ragazza avrà un’età EF = AB + 11, l’altra GH = CD + 11,
cioè EFGH = ABCD + 1111.
Dopo 11 anni si avrà che
√ABCD + 11 = √(ABCD + 1111) (1)
pongo √ABCD = x (allora x sarà un numero di 2 cifre compreso uguale tra 32 e 99)
e la (1) si potrà scrivere: x + 11 = √(x^2 + 1111)
quadrando entrambi i membri:
(x + 11)^2 = x^2 + 1111 → x^2 + 22x + 121 = x^2 + 1111
le due incognite al quadrato si annullano e raggruppando al primo membro il termine con l’incognita e al secondo i termini noti:
22x = 1111 – 121 → 22x = 990 → x = 990 / 22 = 45
ma poiché si era posto √ABCD = x → ABCD = x^2 = 45^2 = 2025
Quindi una ragazza ha 20 anni (AB = 20) l’altra 25 (CD = 25)
√2025 = 45
Tra 11 anni la prima ragazza ne avrà 20 + 11 = 31 (EF = 31) l’altra 25 + 11 = 36 (GH = 36)
√3136 = 56
...son proprio stupidino! È la (1) di Andy che non capisco. Per 'dimostrare' la (1) ho fatto quella stramba somma di 11 numeri dispari tra 91 e 111... Mah! Spero che qualcuno me la spieghi. O la (1) è evidente a tutti ma non a me?
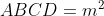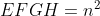Se
, 
e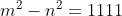 
allora
quindi devono valere queste due relazioni che formano un sistema di 2 equazioni in 2 incognite
La soluzione di questo sistema è (fortunatamente) fatta da interi
Poichè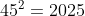
Le età di Anna e Bruna dovrebbero essere rispettivamente di
20 e 25 anni
Per controprova sommo a ciascuna 11 ed ottengo 31 e 36 e
3136 è proprio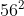
Scusate, le prime due relazioni sono invertite
Ecco come si fa, bravo Fabrizio!
Sapevo che si poteva far meglio del brutto pasticcio che ho fatto io!
Probabilmente il quiz rappresenta un caso particolare di una regola generale:
Ponendo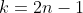
, k rappresenta il numero di anni affinché una coppia di età (2 cifre per coppia, AB e CD) iniziali che "affiancate" (ABCD) formano un quadrato perfetto, dopo un k numero di anni formano un'altra quadrupla (EFGH) di 2 coppie (EF e GH) affiancate.
Una tabella visualizza meglio:
con la quadrupla in rosso che indica la coppia di età affiancate e la quadrupla in verde la coppia che rappresenti un quadrato perfetto dopo k anni.
Le ultime 2 colonne confermano quanto scritto da Fabrizio, ovvero che la somma delle radici di ABCD e EFGH si ripete secondo la costante 101, mentre la differenza tra le radici è pari al numero k di anni.
Il limite di n = 9 e di conseguenza k = 17 è dovuto al fatto che se n = 10 → k = 19
si avrebbe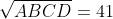
→ 
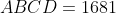cioè la coppia di età iniziali è 16 e 81, ma aggiungendo il valore di k = 19 le età diverrebbero 35 e 100 che affiancate (35100) eccedono il limite di 4 cifre imposto dal quiz, anche se matematicamente l'equazione viene rispettata
( n = 10 → k = 19 , 19 × 101 = 1919 , x = 41 ,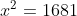
, 
, 
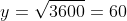
y + x = 101 , y - x = k = 19).
Grande Andy! Nelle tue mani anche un semplice quiz riesce a dar luogo a generalizzazioni veramente interessanti.
OK, OK... bravi Fabrizio e Francesco e, ovviamente, anche Andy