23/10/22

AROGATIP *

Categorie: Matematica Tags: generalizzazione geometria poligoni simili teorema di Pitagora Scritto da: Vincenzo Zappalà Commenti:15

Non vi spaventi il titolo... basta pensarci un po' e salta all'occhio che non è altro che il nome Pitagora al contrario. Il perché è nato da un suggerimento del nostro amico Frank che ho accolto senza titubanze. In realtà, il tutto sta a significare che ho ideato (magari non sono il primo...) una dimostrazione del famoso teorema, proprio lavorando... al contrario.

Il teorema di Pitagora è probabilmente il teorema più conosciuto e usato in geometria. Esso era sicuramente noto ben prima di Pitagora, sia tra i babilonesi che tra i cinesi, gli indiani e gli antichi egizi. Tuttavia, la sua prima dimostrazione sembra essere quella di Pitagora e, quindi, accettiamo pure il suo nome.

Oggi, si contano più di cento dimostrazioni differenti del teorema, tra cui quelle date da persone completamente diverse, come Einstein e un presidente degli Stati Uniti (QUI). Alcune di queste dimostrazioni sono più o meno eleganti, altre più o meno complicate, ma potremmo chiederci: "Qual è la più rapida di tutte?".

Bene, ciò che sto per descrivere è probabilmente la più breve in assoluto. Anzi, voglio dimostrare che il teorema di Pitagora nasce direttamente come caso particolare di qualcosa di ben più generale.

Accettiamo per buoni che la similitudine dei poligoni e il calcolo dell'area del triangolo siano cosa ben note e, allora, partiamo proprio da una conseguenza facilissima da dimostrare (lo faremo in appendice): le aree di due poligini simili stanno tra loro come i quadrati dei lati corrispondenti.

Ne segue, immediatamente che

A1/A2 = d1²/d2²

Bene questa è già una versione del teorema di Pitagora. Conoscendo lei vuol dire dimostrare il teorema di Pitagora nella sua versione più generale. Non stupitevi, ma è proprio così.

Consideriamo infatti tre segmenti di dimensioni crescenti, tali che:

d1 ≤d2 <d3

ed essi siano i lati corrispondenti di tre poligoni simili qualsiasi. Possiamo scrivere:

A1/A3= d1²/d3²

A2/A3 = d2²/d3²

sommando:

(A1 + A2)/A3 = (d1² + d2²)/d3²

Scelti d1, d2 e d3 possiamo concludere che il secondo membro è una costante per qualsiasi poligono si sia scelto costruibile sui tre segmenti.

Questa conclusione va, ovviamente, considerata come nozione già acquisita a priori, basandosi solo su aree e su similitudini. Ma è proprio lei che ci dimostra immediatamente il teorema di Pitagora. La (1), infatti, ci dice che la somma di due aree diviso la terza è indipendente dalla forma del poligono costruita sui segmenti corrispondenti.

Ma, cosa succederebbe se A1 + A2 fosse uguale ad A3? Bene, sarebbe valida per qualsiasi tipo di poligono.

Non ci resta che prendere un qualsiasi triangolo rettangolo e tracciare la perpendicolare dal punto in cui si trova l'angolo retto fino all'ipotenusa, come mostra la Fig. 1.

Non ci resta, adesso, che ribaltare i due triangoli minori e quello completo (ma se ne potrebbe anche fare a meno) e notare che i tre triangoli così ottenuti sono simili tra loro e che la somma dell'area A1 e dell'area A2 è proprio uguale all'area A3. Ma se sono simili deve anche valere la (1), ossia: la somma dei poligoni costruiti sui cateti è uguale al poligono costruito sull'ipotenusa (poligoni simili, ovviamente). Ne segue che questa conclusione vale per qualsiasi poligono e, quindi, anche per il quadrato.

Voglio ancora rimarcare che, normalmente, prima si dimostra il teorema di Pitagora per il quadrato e poi si generalizza ad ogni tipo di poligono (ma anche a figure curvilinee qualsiasi). Noi, invece, abbiamo dimostrato immediatamente il caso generale e poi considerato il teorema di Pitagora come caso particolare.

A questo punto lascio un piccolo compitino ai nostri mate-moschettieri: La relazione precedente potrebbe anche valere per una figura con un numero di lati qualsiasi, ossia potremmo generalizzare il tutto dicendo che: dato un poligono qualsiasi, di n lati, la somma delle aree di qualsiasi poligono costruite su di loro potrebbe essere uguale all'area del poligono costruito sul lato maggiore (o qualcosa del genere). Chissà se può capitare... lascio ai mate-moschettieri (ma non solo, ovviamente) qualsiasi tentativo di risposta (non l'ho ancora studiata per bene, ma mi appare impossibile...).

Appendice:

Dati due poligini simili, le loro aree stanno nello stesso rapporto dei quadrati di due lati corrispondenti.

Dimostrazione:

Qualsiasi poligono può essere diviso in triangoli, per cui basta dimostrare la tesi nel caso di due triangoli.

Consideriamo due triangoli simili di aree A1 e A2, mentre d1 e d2 sono due lati corrispondenti (Fig. 2).

Come ben sappiamo se due triangoli sono simili il rapporto tra le altezze è uguale al rapporto tra i lati, per cui:

d1/d2 = h1/h2 .... (2)

Sicuramente è anche valida l'identità:

d1/d2 = d1/d2

Facciamone il prodotto:

d1²/d2² = (h1 d1)/(h2 d2) = 2A1/2A2 = A1/A2

c.v.d.

15 commenti

Andy

25/10/2022 at 00:14
Caro Enzo,

se non ho interpretato male, se si assume che: "dato un poligono qualsiasi, di n lati, la somma delle aree di qualsiasi poligono costruite su di loro potrebbe essere uguale all'area del poligono costruito sul lato maggiore", affinché ciò sia possibile, deve essere soddisfatta la condizione:

$\sqrt{{a{_1}^2}+a{_2}^2+a{_3}^2+....+a{_{n-1}}^2} = b$

dove b è il lato maggiore e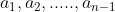 $a_1,a_2,.....,a_{n-1}$ sono gli altri lati

(ovviamente con $b<a_1+a_2+.....+a_{n-1}$ affinché la poligonale sia chiusa)

questo potrebbe avvenire a condizione che il poligono qualsiasi (con n > 3):
1. sia scaleno
2. non possieda assi di simmetria
3. non presenti lati paralleli
le condizioni dovrebbero essere necessarie, non so se sufficienti.

per n = 4 , ho trovato alcune "quaterne pitagoriche" che rispettano la condizione, ad esempio

(1, 4, 8, 9) ; (2, 3, 6, 7) ; (2, 5, 14, 15) ; ecc...

come si vede, i poligoni possono essere sia concavi che convessi, e la condizione di perpendicolarità tra due lati non contrasta con l'assunto iniziale. Ho disegnato solo alcune configurazioni, ma "smontando" e "rimontando" i lati secondo angoli sempre differenti, si dovrebbero ottenere innumerevoli poligoni con una specifica quaterna (pitagorica o con radici).

Probabilmente, così come il numero di terne pitagoriche tende all'infinito, lo stesso dovrebbe essere per le quaterne.

Per n = 5 ho solo disegnato un'immagine, ma non ho approfondito (anche se, per estensione, potrebbe essere valido il ragionamento sin qui fatto)
Vincenzo Zappalà

25/10/2022 at 08:12

Beh... direi che abbiamo esteso il teorema di Pitagora esteso... penso che ci sia modo di lavorarci sopra parecchio. Chissà se vale per qualsiasi numero di lati e se vi deve essere un legame tra loro? Mi affido a te - se vuoi e puoi, ovviamente!
Andy

25/10/2022 at 17:18

Forse un altro passettino in avanti:

la condizione che supponeva il poligono scaleno, cessa di essere valida perché vi possono essere quadrilateri con 2 lati uguali e rispettare lo stesso l'assunto iniziale:

sembrerebbe che possa valere l'identità:

$\sqrt{k^2 + m \times (2k)^2 + (2 m k)^2} = k(2m+1)$ con m = n - 3 e k = lato minore

per esempio nella prima figura k = 2 → m = 1

$\sqrt{2^2 + 1 \times (2 \times 2)^2 + (2 \times 1 \times 2)^2} = 2(2 \times 1 +1)$ ↔ $\sqrt{2^2 + 4^2 + 4^2} = 6$

nella seconda k = 3 → m = 1

$\sqrt{3^2 + 1 \times (2 \times 3)^2 + (2 \times 1 \times 3)^2} = 3(2 \times 1 +1)$ ↔ $\sqrt{3^2 + 6^2 + 6^2} = 9$

Per un poligono a 5 lati con 2 lati uguali:

m = 5 - 3 = 2 e k = 3

$\sqrt{3^2 + 2 \times (2 \times 3)^2 + (2 \times 2 \times 3)^2} = 3(2 \times 2 +1)$ ↔ $\sqrt{3^2 + 6^2 + 6^2 + 12^2} = 15$

Provo per un poligono a 6 lati di lato minore 5

m = 6 - 3 = 3 ; k = 5

$\sqrt{5^2 + 3 \times (2 \times 5)^2 + (2 \times 3 \times 5)^2} = 5(2 \times 3 +1)$ ↔ $\sqrt{5^2 + 10^2 + 10^2 + 10^2 + 30^2} = 35$

ma stavolta i lati uguali tra loro diventano 3.

Sembrerebbero tutti casi particolari (anche se numerosi), perché i lati sono multipli tra loro, quindi probabilmente per un poligono d n lati, data la dimensione del lato minore, si avrebbe una somma di quadrati pari a quello del lato minore più n-3 volte il suo doppio più 2(n - 3) volte la sua misura. Il lato maggiore sarebbe 2(n - 3) + 1 volte il minore.

Giusto per curiosità: poligono di 7 lati, lato minore 7, m = 4 (allora 4 lati uguali)

$\sqrt{7^2 + 14^2 + 14^2 + 14^2 + 14^2 + 56^2} = 63$
Vincenzo Zappalà

25/10/2022 at 18:13

ti sto seguendo con molta attenzione... come hai tirato fuori la radice? E se ci fossero due lati minori uguali?

Forse si potrebbe iniziare a lavorare solo sulle quaterne e studiare tutti i casi possibili. Vedi tu... il teorema di Andy sta formandosi
Vincenzo Zappalà

25/10/2022 at 18:19

In altre parole: per le terne il triangolo deve essere rettangolo. E per le quaterne, qual è la condizione? Di sicuro non può avere un angolo retto.
Andy

25/10/2022 at 23:21

La radice è "figlia" di numerosi tentativi "sperimentali"; ero partito dall’ipotesi del lato minore unitario, e facendo varie prove con numeri piccoli:

$1^2+2^2+2^2 = 3^2$

Però ho anche notato, procedendo sempre per tentativi e con valori gradualmente più grandi, che secondo e terzo addendo del primo membro “giravano” secondo un numero costante che ho scoperto poi fosse il numero di lati meno 3: quindi per un quadrilatero m = 4 – 3 = 1;

per cui, con numeri leggermente maggiori, sono passato a 2 come lato minore:

$2^2 + m(2 \cdot 2)^2 + (2\cdot m \cdot 2)^2$ , ma m = 1 quindi: $2^2 + (2 \cdot 2)^2 + (2\cdot 2)^2$ = $2^2+4^2+4^2=6^2$

con lato minore 3:

$3^2 + m(2 \cdot 3)^2 + (2\cdot m \cdot 3)^2$ → $3^2 + 1(2 \cdot 3)^2 + (2\cdot 1 \cdot 3)^2$ = $3^2 + 6^2 + 6^2 = 9^2$

ovviamente estraendo la radice quadrata della somma dei quadrati, ottengo la radice quadrato dell’ultimo lato (che è quello maggiore perché somma di 3 quadrati minori).

Successivamente, ho potuto sperimentare che l’algoritmo sembrava funzionare anche per poligoni con un numero di lati maggiore a 4, dove la misura dei lati mediani si ripeteva costantemente secondo multipli del lato minore e da questo è nata la formula sotto radice

$\sqrt{k^2 + m \times (2k)^2 + (2 m k)^2} = k(2m+1)$

es., per un poligono a 100 lati di lato minore 11, m = 97:

$\sqrt{11^2 + 97 \cdot (2 \times 11)^2 + (2 \times 97 \times 11)^2} = 11(2 \times 97 + 1)$ →

$\sqrt{11^2 + 97 \cdot 22^2 + 2134^2} = 2145$

Se ci fossero i due lati minori uguali non ho verificato, ma se non venisse fuori la quaterna pitagorica, considerando il terzo lato intero, l'ultimo lato avrebbe comunque un valore sotto radice, seguendo sempre il teorema di Pitagora:

Ma forse ho trovato l’algoritmo che genera quadruple pitagoriche di numeri non tutti multipli tra loro, in base ad una congettura: considero il lato minore 2, poi il primo dei lati mediani pari ad un numero dispari superiore a 2, e sempre per tentativi, ottengo queste quadruple:

2 3 6 7

2 5 14 15

2 7 26 27

2 9 42 43

Chiamando con a1, a2, a3 e a4 i termini della quadrupla, con n il primo dei numeri naturali positivi (funge da contatore) e partendo dalla prima:

per n = 1: a1 = 2, a2 = 2n+1 = 3, a3 = 2(2×1+1) = 6, a4 = a3 + 1 = 7

per n = 2: a1 = 2, a2 = 2n+1 = 5, a3 = 2(2×3+1) = 14, a4 = a3 + 1 = 15

per n = 3: a1 = 2, a2 = 2n+1 = 7, a3 = 2(2×6+1) = 26, a4 = a3 + 1 = 27

per n = 4: a1 = 2, a2 = 2n+1 = 9, a3 = 2(2×10+1) = 42, a4 = a3 + 1 = 43

per n = 5: a1 = 2, a2 = 2n+1 = 11, a3 = 2(2×15+1) = 62, a4 = a3 + 1 = 63

…...

Noto che nel termine a3 il moltiplicatore del 2 dentro parentesi varia in sequenza 1, 3, 6, 10, 15,…

che è la stessa sequenza della regola di Gauss per il calcolo della somma dei primi n naturali: n(n+1)/2;

allora sostituendo questo formula dentro la parentesi che fa da moltiplicatore per determinare a3:

2(2×n(n+1)/2 +1) = 2( n·(n+1) + 1);

per esempio:

per n = 8; a1 = 2, a2=2×8+1 = 17, a3 = 2(8×9+1) = 146, a4 = 147

$2^2+17^2+146^2=147^2$

Dovrebbe funzionare per ogni n positivo, per cui si dovrebbero avere un numero di quadruple che tende all’infinito e di conseguenza anche un numero → ∞ di quadrilateri scaleni ai quali è applicabile il teorema di Pitagora esteso.

L'angolo retto non dovrebbe ostacolare la formazione di quadrilateri dotati di quadrupla pitagorica:
Vincenzo Zappalà

26/10/2022 at 09:03

Sull'angolo retto hai pienamente ragione... Anzi, è proprio lui che permette la seguente costruzione geometrica...

Anche questo mi sembra un passo geometrico in avanti...
Vincenzo Zappalà

26/10/2022 at 09:22
Vincenzo Zappalà

27/10/2022 at 17:48

ERRATA CORRIGE:

Nel commento del 26, ore 9:03, nella seconda figura, l'ultima riga va letta:

a² + b² + d² + f² = g²
Andy

27/10/2022 at 19:59

Ok, ma mentre per un triangolo condizione indispensabile e unica affinché sia applicabile il teorema di Pitagora è che contenga un angolo retto, nel caso dei quadrilateri tale condizione non è unica perché si è visto che possono o meno contenerlo, possono essere sia concavi che convessi, ed essere lo stesso pitagorici.

Se si parte da un triangolo rettangolo, si ottengono per costruzione (con la condizione di perpendicolarità all'ipotenusa di un segmento passante per il vertice opposto a quello che contiene l'angolo retto) quadrilateri pitagorici, ma lo stesso si ottiene se si usa come condizione il fatto che se il quadrilatero possiede un lato di misura pari e un secondo lato di misura dispari (e viceversa), e viene essere soddisfatta l’equazione generale:

$\sqrt {a^2 + b^2 + c^2} = d$ ponendo la condizione d = c + 1,

per cui l’equazione precedente diventa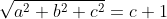 $\sqrt {a^2 + b^2 + c^2} = c + 1$ e sviluppando si otterrà

$c = \frac{a^2 + b^2 - 1}{2}$

allora è pitagorico;

es.: a = 1 , b = 2 , → c = 2 , d = 3

a = 6 , b = 11 , → c = 78 , d = 79

a = 2 , b = 13 , → c = 86 , d = 87

a = 7 , b = 10 , → c = 74 , d = 75

a = 10 , b = 19 , → c = 230 , d = 231

Nel primo esempio, si può notare che i lati mediani sono uguali, e questo può avvenire se i due lati mediani sono il doppio del lato minore e di conseguenza il lato maggiore è il triplo del lato minore:

$\sqrt {a^2 + b^2 + c^2} = d$ con b = c = 2a → $\sqrt {a^2 + (2a)^2 + (2a)^2} = 3a$

e in questo caso, i requisiti sono soddisfatti anche per a numero reale positivo non intero;

ma si possono ottenere quadrilateri pitagorici anche se i lati uguali sono i minori, partendo sempre dall’equazione generale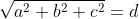 $\sqrt {a^2 + b^2 + c^2} = d$ ponendo le condizioni a = b e d = c + 2 cioè

$\sqrt {a^2 + a^2 + c^2} = c + 2$ sviluppando si avrà che $c = \frac{a^2 - 2}{2}$

es.: a = 4 , b = 4 , → c = 7 , d = 9

a = 12 , b = 12 , → c = 71 , d = 73

come è facile notare, per ottenere numeri interi, a deve essere intero pari.

E tutto ciò è limitato dal fatto di voler ricercare solo valori di misura interi, perché nulla impedisce di avere quadrilateri con uno o più lati di misura differente dai numeri interi ed essere pitagorici.

Quella che comanda è la regola generale:

$\sqrt{{a{_1}^2}+a{_2}^2+a{_3}^2} = a_4$

se le misure dei lati la rispettano allora il quadrilatero è pitagorico, altrimenti no.

Sicuramente non possono essere quadrilateri pitagorici il quadrato, il rettangolo, il parallelogramma, il rombo, il deltoide.
Andy

28/10/2022 at 00:12

Limitatamente alle n-uple pitagoriche, per il caso generale:

se indico con $n$ il numero di lati di un poligono ( $n> 3$ ),

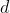con $d$ un qualsiasi intero dispari, con 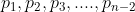$p_1,p_2,p_3,....,p_{n-2}$ una serie di interi pari qualsiasi (un singolo 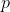$p$ può anche ripetersi più volte), la n-upla deve soddisfare la condizione:

$\sqrt {d^2 + p_1 ^2 + p_2 ^2 + p_3 ^2 + ....+ p_{n-2} ^2 + m^2} = m + 1$

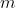con $m$ che è un intero pari;

elevando tutto al quadrato: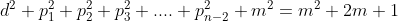 ${d^2 + p_1 ^2 + p_2 ^2 + p_3 ^2 + ....+ p_{n-2} ^2 + m^2} = m^2 + 2m + 1$

eliminando i due $m^2$ al primo e al secondo membro e isolando $m$

$m = \frac{d^2 + p_1 ^2 + p_2 ^2 + p_3 ^2 + .... + p_{n-2} ^2 - 1}{2}$

Es.: per un ennagono di lati 3, 2, 8, 14, 22, 6, 4, m, m + 1

$m = \frac{3^2 + 2^2 + 8^2 + 14^2 + 22^2 + 6^2 + 4^2 - 1}{2} = 404$

la condizione è verificata: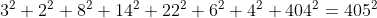 ${3^2 + 2^2 + 8^2 + 14^2 + 22^2 + 6^2 + 4^2 + 404^2} = 405^2$
Vincenzo Zappalà

28/10/2022 at 08:10

Sì, vi sono vari modi per ottenere il risultato voluto. Quello da me proposto è puramente grafico e mi ha fatto riscoprire un teorema greco che non conoscevo...

Io penso di scrivere qualcosa a riguardo, mentre a te chiedo di cercare di riunire il tutto in una visione generale, sia per interi che per non interi. Cerca, però, di non eliminare passaggi e di non dare conclusioni che non siano spiegate molto semplicemente. Pensiamo a chi è diretto, mi raccomando...
Andy

29/10/2022 at 12:11

Su invito di Enzo,

ho cercato di creare un quadro generale ma sintetico e più ordinato, limando inesattezze ed eliminando errori presenti nei miei interventi precedenti.

Ogni osservazione e correzione è ben gradita!
Vincenzo Zappalà

29/10/2022 at 15:29

Ottimo Andy! Vale proprio la pena di pubblicare questa trattazione come articolo del blog. Se mandi la versione originale a Daniela lei riuscirà a riportarla come articolo. Temo solo che per il latex esistano i problemi che conosciamo (ossia spariscono dopo un po'). Ma le formule si possono facilmente scrivere normalmente.

Mancherebbe solo un "cappello" iniziale che spieghi molto semplicemente cosa si intende trattare e un minimo di conclusioni. Sempre che tu voglia, ovviamente... e che lo voglia anche Dany
Daniela

29/10/2022 at 17:06

Andy invia l'articolo definitivo a infinitoteatrocosmo@gmail.com e vediamo di trovare il modo tecnicamente migliore per pubblicarlo.

Riguardo a Latex, meglio lasciare perdere... non esiste più la possibilità di scrivere formule sulla piattaforma online e di trasferirle negli articoli: lo usa mia figlia per elaborare testi matematici in ambito universitario ed è un vero e proprio linguaggio di programmazione decisamente laborioso sia da installare che da usare.

Lascia un commento Cancel Reply

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.

AROGATIP *

Articoli correlati

Soluzione (una delle tante possibili) al problema del numero primo ****

Facciamo sul serio ... ****

La spirale aurea è un nostra creazione... accontentiamoci dei numeri irrazionali **

Un problema “olimpico” abbastanza complicato ***

15 commenti

Lascia un commento Cancel Reply