Vogliamo proporvi un simpatico problema che ha attirato l'attenzione di matematici per molti anni e che per varie volte ha visto migliorata la sua conclusione. Probabilmente si può fare ancora di meglio...

Il problema è molto semplice:

Un pescatore si dirige al largo in modo rettilineo, perpendicolarmente alla costa, ma, giunto esattamente a 1 km dal punto di partenza, cala improvvisamente una fittissima nebbia e il pescatore non riesce a vedere niente anche alla distanza di un solo metro. Egli non ha a disposizione apparati radar o cose del genere e può solamente misurare con precisione un'eventuale rotazione dell'asse della barca oltre che la distanza che percorre. Purtroppo nel momento in cui cala la nebbia la barca ruota un po' su stessa e quindi la direzione in cui stava puntando prima del calar della nebbia è andata perduta. In poche parole, non può ruotare esattamente di 180° e tornare sui suoi passi.

Quale strategia può utilizzare per tornare a riva?

Bene, la più ovvia e sicura è quella di dirigersi in una direzione qualsiasi e percorrere esattamente 1 km. Poi ruotare la barca di 90° e descrivere un cerchio attorno al punto in cui era calata la nebbia. Quest’ultima operazione non è del tutto ovvia, ma l’esperienza del pescatore la consente.  Alternativamente, avendo sempre a bordo chilometri di corda, poterebbe calare l’ancora e poi muoversi circolarmente, mantenendo tesa la corda. Succede qualcosa come quello che riportiamo in Fig. 1.

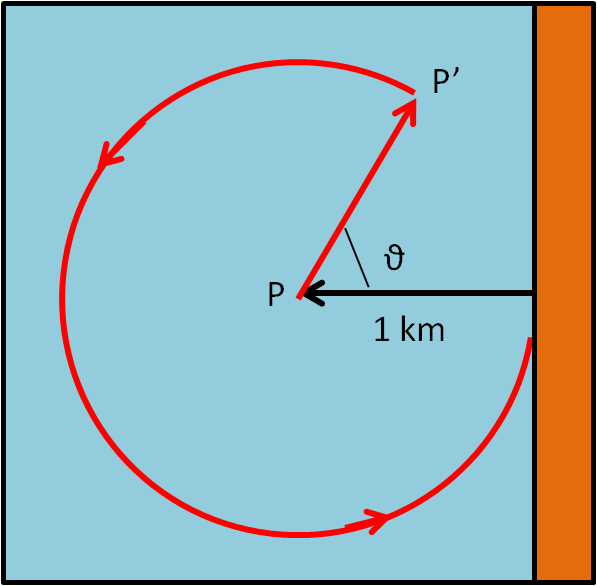
Il pescatore da P va al punto P', che dista 1 km da P, e poi si muove di moto circolare attorno a P. Nel caso della figura se gira verso destra arriva velocemente alla riva, mentre se gira verso sinistra è obbligato a fare un percorso più lungo, ma il ritorno è assicurato.

Il problema, però, è un altro: lui non ha carburante a disposizione per il caso più sfortunato. Infatti, il pescatore ha carburante solo per un percorso di 6.4 km. Qual è questo caso? È facile descriverlo in Fig. 2.

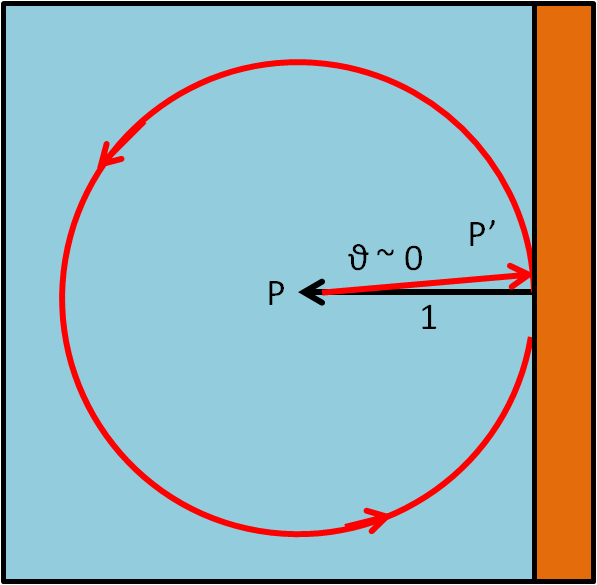
Il pescatore si dirige quasi esattamente verso il punto di partenza e, dopo 1 km, si trova QUASI a riva, ma la nebbia non gli permette di scorgerla. Cosa fare? Beh, come già detto, ruotare la barca di 90° in una direzione qualsiasi. Nel caso più sfortunato fa il percorso verso sinistra che lo costringe a compiere praticamente tutta la circonferenza di raggio 1 km e di centro P. In altre parole, il percorso s più sfortunato risulta essere:

s = 1 + 2π = 7.28 

In questo caso sfortunato il carburante non basta. Deve cercare una strategia che, anche nel caso peggiore, gli permetta di compiere un tragitto più corto.

Un miglioramento è senz’altro quello di percorrere un arco minore di quello di Fig. 2. Basta infatti che dopo 270° di percorso curvilineo prosegua per la tangente (Fig. 3)

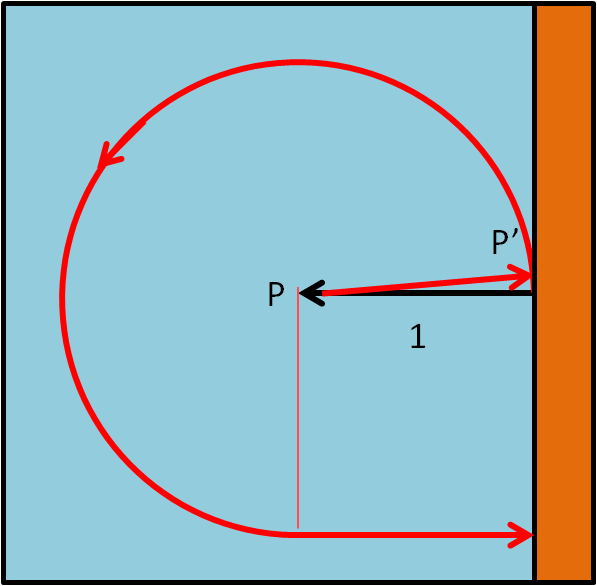
In tal caso s si riduce a:

s = 1 + (3/2)π + 1 = 6.71

Un bel miglioramento ma ancora non basta. Notiamo bene che per una direzione iniziale qualsiasi la configurazione della rotta da seguire non cambia e, ovviamente, il percorso risulta sempre minore, di quello più sfortunato, come mostra l’animazione che segue.

 

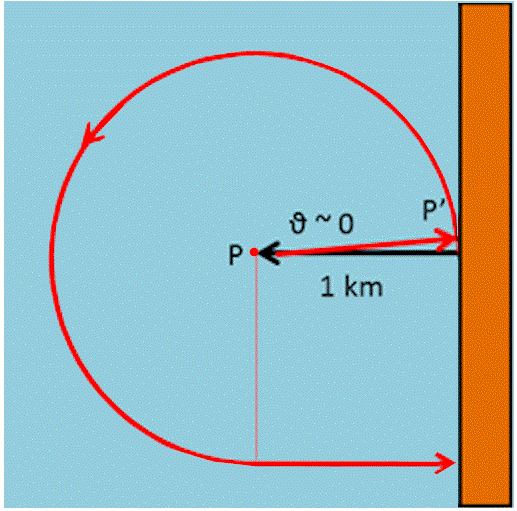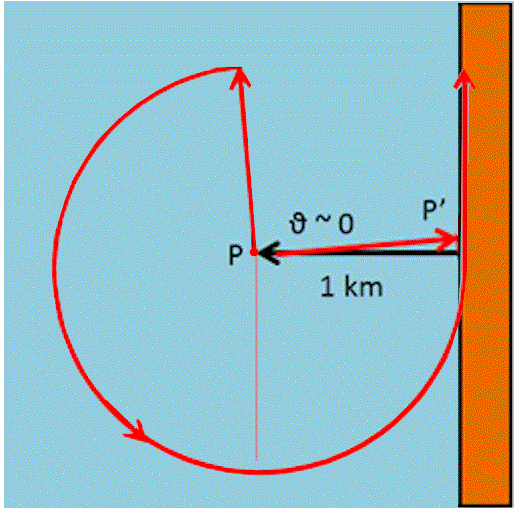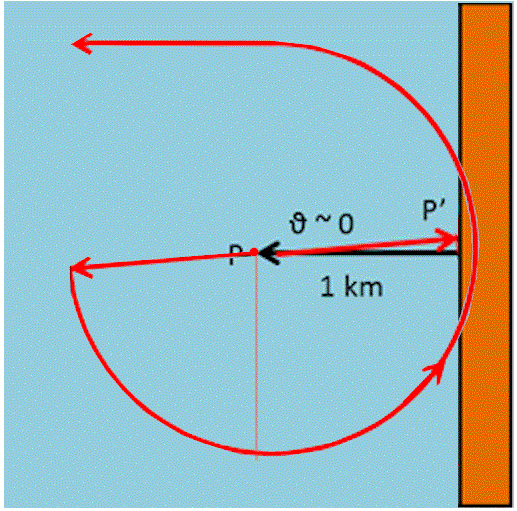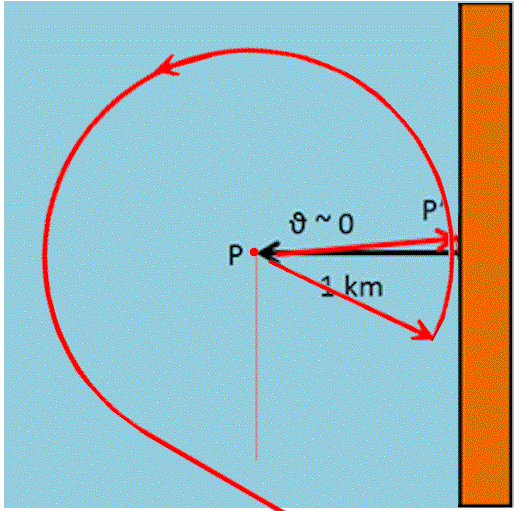
Seconda strategia  

La barca si dirige nuovamente verso una direzione qualsiasi, ma aumenta il raggio, ossia percorre una certa distanza d > 1. Nuovamente, il caso più sfortunato è quello in cui, pur aumentando il percorso d si viene a trovare vicinissimo alla riva. Le cose sembrano peggiorate, dato che deve nuovamente ruotare la barca di 90° e iniziare il suo percorso circolare con un raggio maggiore. Tuttavia, deve percorrere un arco minore di 270°, dato che parte da un angolo ϑ maggiore di zero. Cosa succede, in questo caso? Aumentando il tragitto iniziale il pescatore aumenta anche il raggio del cerchio e quindi l’arco da percorrere; tuttavia, quest’ultimo, corrisponde ad un angolo minore.

La situazione viene illustrata in Fig. 4.

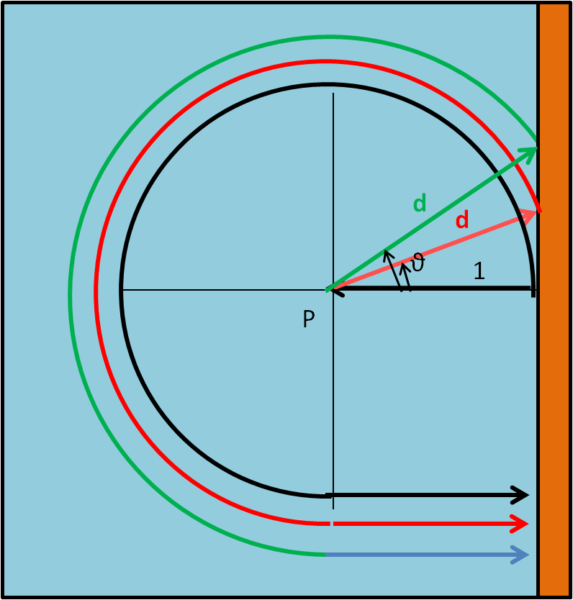
La strategia è una sola, ma le configurazioni dipendono dalla scelta di d e, di conseguenza, dell’angolo ϑ.

s  = d + d((3/2)π – ϑ) + 1

Ma d = 1/cos ϑ

Per cui ϑ = arccos (1/d)

Il percorso diventa:

s  = d + d((3/2)π – arcos (1/d)) + 1

Questa è una funzione di d, per cui è possibile metterla in grafico e calcolare il valore minimo di s ottenibile al variare di d. In altre parole, si cerca un d > 1 che permetta di compiere un percorso minore pur nelle peggiori condizioni. La Fig. 5 riporta la funzione s(d):

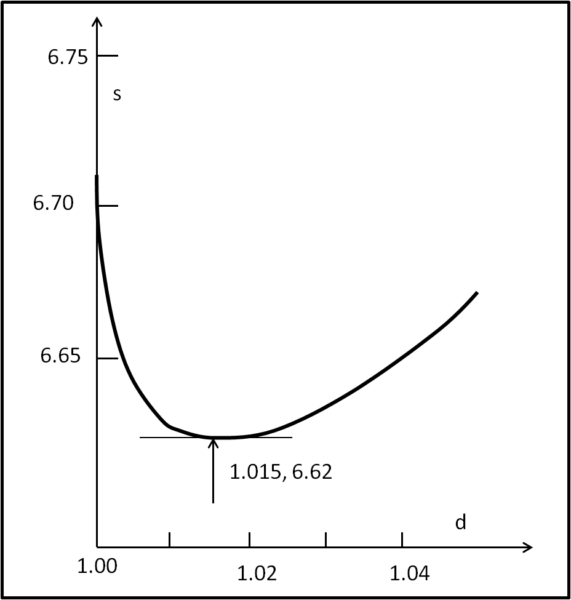
Non ci stupisce certo il fatto che per un angolo di 0° si ottiene di nuovo s = 7. 21. Il minimo si ha per d = 1.015 e questo minimo vale 6.62, minore del 6.71, ottenuto con la strategia precedente. Un valore di d = 1.015 comporta un angolo di

 ϑ = 10°

Come si traduce praticamente questo risultato? La barca si dirige verso una direzione qualsiasi per una lunghezza d = 1.015. Poi ruota di 90°, gira per 270° – 10° = 260° e, infine, va dritta per la tangente. Nel caso più sfortunato il percorso è di 6.62 km (Fig. 6).

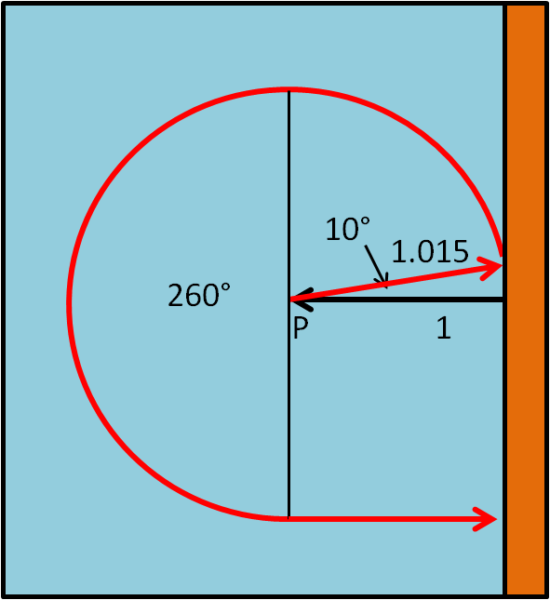
Tutto si accorcia partendo da una direzione qualsiasi diversa da 10°, come mostra l’animazione.

Purtroppo, però, il percorso è ancora troppo lungo per il carburante a disposizione. Dobbiamo fare di meglio.

Riuscite a immaginare una strategia migliore? Bene, descrivetela nei commenti e non andate avanti a leggere. Chi, invece, non si vuole mettere alla prova può continuare …

Terza strategia

La barca si dirige nuovamente verso una qualsiasi direzione e ha la solita sfortuna di avvicinarsi moltissimo alla riva, senza poterla vedere. Poco male. Chiamiamo nuovamente θ l'angolo che la direzione presa fa con la linea orizzontale. Ne segue che il primo tratto rettilineo compiuto dalla barca risulta essere √(1 + tan²θ). A questo punto ruotiamo la barca, rispetto alla direzione iniziale, di 90° - θ e avanziamo di tan θ, come mostra la Fig. 7

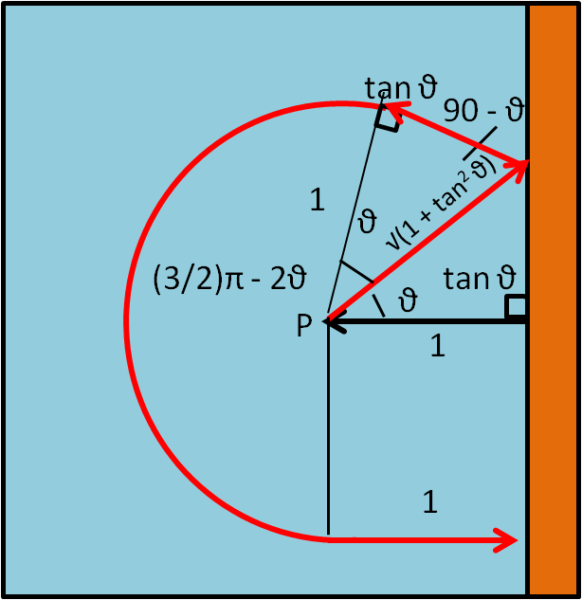
Dopo questa operazione la barca si ritrova a una distanza 1 rispetto al punto d'inizio e può iniziare il suo moto circolare che finisce dopo 270 - 2ϑ, quando può proseguire per la tangente. Il percorso risulta essere:

s = √(1 + tan²ϑ) + (3/2)π - 2 ϑ + tan ϑ + 1

Non ci resta che fare il grafico di questa funzione e cercare il valore di θ che dia s minimo. Otteniamo la Fig. 8

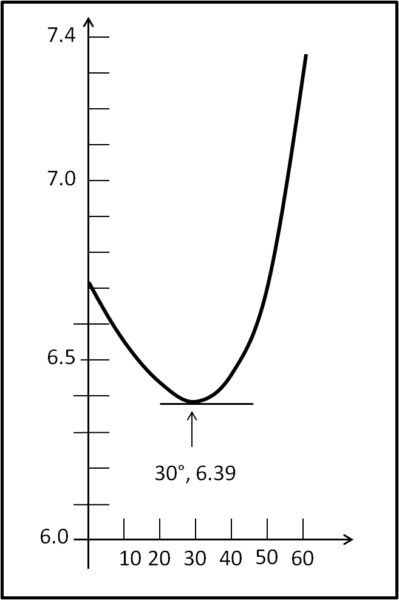
Il minimo esiste, corrisponde a un angolo θ = 30° e comporta un percorso d di soli 6.39 km. Si sceglie quindi l’angolo di 30° e si procede come illustrato in Fig. 9

Questo è ovviamente il caso più sfortunato. Se la barca si dirige verso una direzione qualsiasi, il percorso risulta decisamente più corto, come mostra la solita animazione: