Introduzione

Il principio su cui si basa l'analisi di Fourier è la constatazione del fatto che spesso in natura un segnale oscillante si presenta non come una oscillazione ad una singola frequenza (o lunghezza d'onda) "pura", ma come una sovrapposizione di frequenze (o lunghezze d'onda) differenti. Esempi classici si trovano nell'ottica (la luce bianca è una sovrapposizione di differenti colori, cioè frequenze, che possono essere decomposte facendo passare la luce attraverso un prisma), in musica (i suoni "armonici" non sono altro che la sovrapposizione di una frequenza fondamentale del suono, con sovrapposte tutte le frequenze multiple della fondamentale), nelle comunicazioni (un segnale radio, o TV, è costituito da un segnale "portante" ad alta frequenza, che serve a trasportare il segnale a grandi distanze, con sovrapposta una modulazione a bassa frequenza, che è il segnale vero e proprio, da filtrare dal resto per poterlo estrarre), ecc.

Lo scopo dell'analisi di Fourier è di dare un metodo per separare le varie frequenze contenute in un segnale e analizzare qual è il contributo delle singole frequenze alla ricostruzione del segnale di partenza.

Premettiamo che attraverso la serie di Fourier si riesce da esprimere una certa funzione PERIODICA attraverso una combinazioni di funzioni trigonometriche. In tal caso compaiono solo sottomultipli del periodo base. Ben diversa è la trasformata di Fourier che permette di fare lo stesso per funzioni non periodiche. Ciò implica che invece di limitarsi a una sommatoria di termini, è obbligatorio scandagliare tutta la gamma di frequenze, anche non intere, attraverso integrali e non sommatorie. Noi ci limiteremo (almeno per adesso) alla serie di Fourier, che  -come vedremo- è già abbastanza “faticosa”.

Come sempre, per poter iniziare una nuova trattazione di matematica non banale, è bene avere a disposizione un buon bagaglio iniziale. E’ proprio per questo che, prima di affrontare la nostra serie, ci dedicheremo alla definizione di funzioni pari e dispari e alle proprietà di ortogonalità delle funzioni trigonometriche .

Funzioni pari e dispari

Data una funzione

y = f(x)

diciamo che essa è una funzione PARI, se:

f(- x) = f(x)

ossia se è simmetrica rispetto all’asse y

Diciamo, invece, che essa è DISPARI se:

f(-x) = - f(x)

ossia se è simmetrica rispetto all’origine degli assi.

Se non sussiste nessuna delle due condizioni la funzione non è né pari né dispari.

Da cosa deriva il nome “pari” e “dispari”? Semplicemente dal fatto che lo sviluppo in serie di Taylor della funzione contiene solo potenze pari o dispari.

Facciamo qualche esempio banale di funzioni pari, dispari e né pari né dispari.

Prendiamo pure la retta più semplice, ossia:

y = x

Applichiamo la condizione di essere pari:

f(-x) è uguale a f(x) ? No, y = -x non è uguale a y = x

la funzione non è pari

y= (-x) è uguale a – y(x)? Sì, - x = - x

la funzione è DISPARI

Passiamo alla parabola:

y = x²

(-x)² = x² ? Sì, la funzione è PARI

L’ovvio risultato si può facilmente vedere. facendo il grafico di alcune funzioni pari e dispari  in Fig. 1.

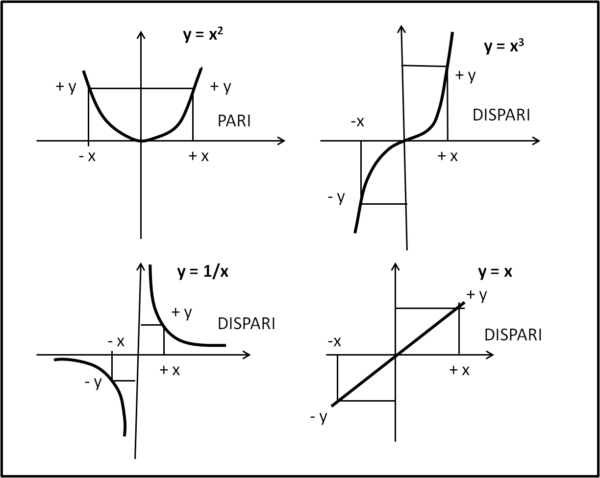
Se prendiamo, invece, la funzione:

y = x + 1

f(-x) = - x + 1 = f(x) = x + 1         NO

f(-x) = - x + 1 = - f(x) = - (x +1) = - x – 1   NO

La funzione non è né pari né dispari.

Un consiglio? Per non confondersi, conviene sempre fare il grafico e vedere direttamente se la simmetria è rispetto all’asse  y, oppure rispetto all’origine o, ancora, non c'è per niente.

Potremmo giocare con qualche polinomio, ma questo è un esercizio che potete fare da soli, ricordando che se l’esponente della x è dispari, la funzione è dispari, mentre se è pari, la funzione è pari. Se vi sono sia termini di grado pari che dispari la funzione non è né pari né dispari.

Vediamo qualche altra funzione, ad esempio:

y = 1/x

Essa è una iperbole e segue che

f(- x) = (1/(-x)) = - 1/x = - f(x)

la funzione è ovviamente dispari.

Proviamo a passare al logaritmo …

y = log (x)

Bene, non possiamo neanche cominciare, dato che non è definito per x < 0.

 

Molto più interessanti per noi sono le funzioni trigonometriche di tipo sinusoidale, ossia il seno e il coseno.

y = sin(x)

f(-x) = sin(- x) = - sin(x) = - f(x)

La funzione è DISPARI

y = cos(x)

f(-x) = cos(-x) = cos(x) = f(x)

La funzione è PARI

Quanto detto si può vedere subito costruendo il cerchio goniometrico o facendo il grafico di y= sin(x) e y = cos(x), come mostrato in Fig. 2.

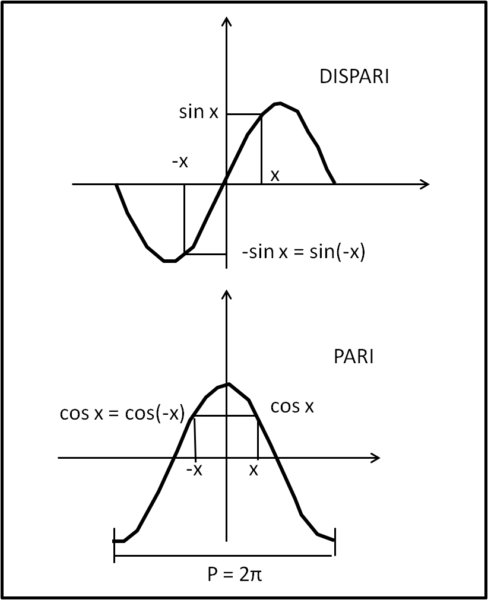
Facciamo, adesso, un passo in avanti e occupiamoci delle operazione tra funzioni pari e dispari.

Consideriamo due funzioni PARI, f(x) e g(x).

Iniziamo con la somma:

Vogliamo sapere se f(x) + g(x) è pari o dispari.

Scriviamo la relazione:

f(-x) + g(-x)

dato che f e g sono pari, possiamo scrivere:

f(-x) + g(-x) = f(x) + g(x)

Ossia cambiando x in – x abbiamo  lo stesso risultato: la somma di due funzioni pari è una funzione pari.

Cosa dire di f(x) – g(x)? Banale …

Scriviamo nuovamente la relazione:

f(-x) – g(-x) = f(x) – g(x)

Anche la differenza è pari.

Passiamo al prodotto:

f(-x) g(-x) = f(x) g(x) dato che sia f che g sono pari.

Cambiando x in – x la funzione prodotto rimane la stessa. Ne segue che anche il prodotto è una funzione pari.

Non ci sarebbe nemmeno bisogno di fare il rapporto, ma trattiamolo per completezza

f(-x)/g(-x) = f(x)/g(x) e quindi il rapporto è una funzione pari.

 

Passiamo alle funzioni DISPARI …

Le funzioni sono dispari, perciò f(- x) = - f(x) e g(-x) = - g(x)

f (-x) + g(-x) = - f(x) + (-g(x)) = - f(x) – g(x) = - (f(x) + g(x))

Cambiando x in – x la somma delle due funzioni cambia di segno quindi la somma è ancora una funzione dispari.

Analogo risultato anche per la differenza.

La somma (e differenza) di due funzioni dispari è una funzione dispari.

Vediamo, invece, il prodotto:

f(-x) g(-x) = - f(x) (- g(x))  = f(x)g(x). Cambiando x in – x il prodotto rimane inalterato.

Il prodotto di due funzioni dispari è una funzione pari

Analogamente lo è anche il rapporto.

 

Una funzione f(x) è PARI e una g(x) è DISPARI

Scriviamo la somma

f(-x) + g(-x) = f(x) – g(x)

non è né pari né dispari

Lo stesso vale per la differenza

Eseguiamo ora il prodotto di una funzioni dispari e di una pari (o viceversa).

f(x)  pari, ossia f(-x) = f(x)

g(x)  dispari, ossia g(-x) = - g(x)

cambiamo x in – x e scriviamo

f(-x) g(-x) = f(x) (- g(-x) = - f(x)g(x)

Il prodotto risulta essere una funzione dispari, infatti cambiando x in – x si ottime il valore negativo del prodotto.

Il tutto può essere facilmente memorizzato, prendendo come funzioni le potenze di x  e ricordando una proprietà del loro prodotto

y = x⁴     y = x²   pari

y = x³    y = x⁵  dispari

Prodotto funzioni pari

x⁴ x² = x^{(4 + 2)} = x⁶              funzione pari

Prodotto funzioni dispari

x³ x⁵ = x^{(3 + 5)} = x⁸               funzione pari

Prodotto funzioni pari e dispari

x⁴ x³ = x ^{(4 + 3)} = x⁷             funzione dispari

Possiamo, perciò, concludere, riguardo alle funzioni trigonometriche, che

sin²x    funzione pari  

cos²x    funzione pari

sin x cos x    funzione dispari

Tanta fatica per così poco? Fidatevi, assimilare benne le proprietà delle funzioni riguardo alla loro parità sembra (ed in effetti lo è) cosa banale, ma spesso sono le cose più banali che creano la maggiore confusione. Disegniamo in Fig. 3 le tre funzioni trigonometriche appena calcolate.

 

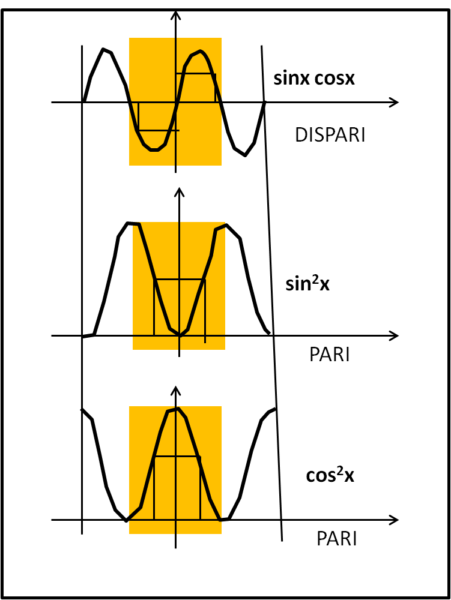
continua...

 

La serie di articoli dedicati alla serie di Fourier è disponibile QUI

e fanno parte del corso completo di matematica