La volta scorsa abbiamo visto come il problema dei cappelli sia risolvibile nel caso di due soli prigionieri. Tuttavia, la strategia usata sembrerebbe applicabile solo a questo caso particolare, in quanto il prigioniero A dice di avere in testa lo stesso cappello di B, mentre B dice di avere in testa un cappello diverso da quello di A.  E se ci fosse un terzo prigioniero C, cosa potrebbe mai dire?

Dobbiamo dimostrare che esiste una strategia risolutiva generalizzabile a qualsiasi numero di prigionieri, in cui rientra anche il caso di due soli prigionieri.

Anticipiamo che la strategia deve essere una e una sola, in modo da poterla decidere prima dell'inserimento dei cappelli, ma tale da essere applicata da ogni singolo prigioniero con uno scopo  diverso (concordato a priori). In tal modo si evitano possibili sovrapposizioni di risultati postivi da parte di più di un prigioniero e, di conseguenza, anche il rischio di non avere nessuna risposta esatta.

Posso anche anticipare che il caso di dieci prigionieri è quello di più facile descrizione, per motivi che vedremo tra non molto. Tuttavia, preferisco partire da due prigionieri proprio per dimostrare che la strategia della volta scorsa può essere descritta in modo diverso e facilmente generalizzabile. Per la spiegazione delle procedure da eseguire sono necessari solo i "concetti" di divisione e resto, oltre che la conoscenza della somma e della sottrazione. Una descrizione veramente alla portata di TUTTI.

Iniziamo introducendo qualche semplice simbolo che ci sarà particolarmente utile.

Chiamiamo con una lettera alfabetica i prigionieri: A e B

Definiamo con un numero il colore dei cappelli. Nel caso di due prigionieri diamo il valore 0 al bianco e  1 al cappello nero. Ovviamente nel caso di due prigionieri, i cappelli in gioco sono solo due: 0 e 1

Chiamiamo SP_A la somma parziale dei numeri dei cappelli che vede il prigioniero A e SP_B quella che vede B.

Nel caso N = 2, le somme parziali di A e di B possono essere solo 0 e 1. In altre parole, qualsiasi sia la configurazione finale, A può vedere solo uno o nessun cappello sulla testa di B. Lo stesso succede per B. Le uniche configurazioni possibili sono, infatti, le quattro che abbiamo analizzato la volta scorsa, ossia: A ha un cappello 0 e B un cappello 1; A ha un cappello 1 e B ha un cappello 0; A e B hanno entrambi un cappello 0; A e B hanno entrambi un cappello 1.

Notiamo che la somma totale ST dei cappelli inseriti sulle teste di A e B può essere 0, 1 o 2, ossia 0 + 0, 1 + 0, 0 + 1, 1 + 1.

A vede SP_A  sulla testa di B. A assume che la ST (che non può conoscere) sia un numero perfettamente divisibile per 2, ossia 0 oppure 2. Ciò implica che se vedesse una SPA = 0, sarebbe obbligato ad avere 0 sulla sua testa, dato che sarebbe l'unico modo per avere una ST uguale a 0 (non potrebbe certo avere un cappello 2, dato che non esiste). Se, invece vedesse una SP_A = 1, sarebbe obbligato ad avere 1 sulla testa, essendo l'unico modo per ottenere una ST  = 2 (non potrebbe certo avere un cappello con valore negativo!). In entrambi i casi otterrebbe un resto della divisione per 2 uguale a ZERO (0 : 2 = 0 con resto 0; 2: 2 = 1 con resto ZERO)

B vede SP_B  sulla testa di A. B assume che la ST (che non può conoscere) sia un numero NON divisibile per 2, ossia 1 . Ciò implica che se vedesse una SP_B = 0, sarebbe obbligato ad avere 1 sulla sua testa, dato che sarebbe l'unico modo per avere una ST uguale a 1. Se, invece vedesse una SP_B = 1, sarebbe obbligato ad avere 0 sulla testa, essendo l'unico modo per ottenere una ST  =  1. Solo agendo in tal modo otterrebbe sempre un resto uguale a UNO (1:2 = 0 con resto  UNO)

Questa strategia è esattamente la stessa che ha avuto successo  la volta scorsa. Proviamo a controllare?

(1) A ha un cappello 0, B ha un cappello 0

A vede una SP_A uguale a 0 e, quindi, ne consegue che è obbligato a dire che anche lui ha 0 sulla testa, in modo da avere come ST proprio 0.

B vede una SPB uguale a 0 e, quindi, è obbligato a dire di avere 1 sulla  testa, in modo da avere come ST 1.

A dice zero e B dice uno. La risposta di A è esatta.

(2) A ha un cappello 1, B ha un cappello 1

A vede una SP_A uguale a 1 e, quindi, l'unico modo per ottenere una ST uguale a 2 è quello di avere anche lui un cappello 1.

B vede una SP_B uguale a 1 e, quindi,  è obbligato a dire di avere zero in testa, in modo da ottenere una ST uguale a 1.

A dice di avere 1 e B dice di avere zero. La risposta esatta è quella di A.

(3) A ha un cappello 0 e B un cappello uguale a 1.

A vede una SP_A uguale a 1 e, quindi, è obbligato a dire di avere in testa 1.

B vede una SP_B uguale a 0 ed è obbligato a dire di avere in testa un cappello 1.

A dice dice di avere uno e B dice di avere in testa uno. La risposta esatta è quella di B.

(4) A ha un cappello 1 e B un cappello uguale a 0.

A vede una SP_A uguale a 0. Non può che dire 0.

B vede una SP_B uguale a 1. Non può che dire o.

A dice di avere 0 e B di avere 0. La risposta esatta è quella di B.

Tutto torna perfettamente: un solo prigioniero dà ogni volta la risposta esatta, proprio come volevamo. Ogni prigioniero adotta la stessa strategia, ossia, fa in modo che il resto della divisione per 2 sia qualcosa di obbligatorio per entrambi, ma il primo ha come resto da ottenere 0, mentre il secondo ha come resto da ottenere 1. Uguale strategia totale di A e B, ma con resto della divisione diverso.

Il risultato è esattamente quello ottenuto la volta scorsa, ma la sua generalizzazione è adesso estremamente  evidente. Basta, infatti, cambiare il resto ogni volta e il numero di prigionieri può essere qualsiasi. Ad, esempio se N fosse 3, A si occuperebbe di dare un risultato che comporti una somma totale divisibile per 3 (resto ZERO), B di ottenere un resto della divisione uguale a UNO, C di ottenere un resto uguale a DUE.

Ogni prigioniero si occuperebbe di un resto diverso. In tal modo tutte le possibilità vengono dichiarate e nessuno può mai dare un risultato che soddisfi più di un solo prigioniero.

Prima di considerare N = 10 (caso più semplice da calcolare!), proviamo con N = 5.

A deve ottenere un resto di 0, B di 1, C di 2 , D di 3 e E di 4. Ovviamente il resto 5 non può esistere dato che N è proprio 5.

Non abbiamo bisogno di ripetere tutti i passaggi eseguiti con 2 prigionieri... Basta fare una semplice tabella per qualsiasi distribuzione C dei 5 cappelli si voglia. I cappelli in gioco sono 0, 1, 2, 3 e 4. Inseriamo 3 su A, 0 su B, 2 su C, 2 su D e 4 su E. Accanto a ogni prigioniero indichiamo il resto R che si è imposto di ottenere.

C    P     R

3    A      0

0    B      1

2    C      2

2    D      3

4    E      4

La somma totale (che può vedere solo il re) è data dalla somma dei cappelli, ossia 11

Ogni prigioniero vede una certa SP. Riportiamola in tabella:

C    P    R         SP

3    A     0    11 - 3 = 8

0    B     1     11 - 0 = 11

2    C     2     11 - 2 = 9

2    D     3     11 - 2 = 9

4    E     4      11 - 4 = 7

Ogni prigioniero calcola il resto della divisione per 5 di SP.

Il prigioniero A deve fare 8: 5. Una divisione che comporta un resto, ossia 8 : 5 = 1 con resto di 3. A, però,  deve fare in modo che il resto venga esattamente 0. Perché  questo sia possibile deve aggiungere alla sua SP il  numero 2, ossia fare 8 + 2 = 10 che è esattamente divisibile per 5. Il suo cappello (Cap) deve, perciò, essere uguale a 2 e lo dice a gran voce .

B deve ottenere un resto di UNO. La sua SP è 11, ossia è un numero che diviso per 5 dà già come resto 1. Questo è proprio quello che si è imposto e B non può che dire di avere un cappello uguale a ZERO.

Il prigioniero C si è imposto un resto di 2. Vede una SP di 9. Per potere avere un resto di 2 deve fare in modo che aggiungendo il suo cappello alla SP ottenga una ST tale da dare un resto di 2 dopo la divisione per 5. Per far ciò deve aggiungere 3 (9 + 3 = 12 che diviso per 5 dà come resto 2). Deve dire che il suo cappello è TRE.

E via dicendo...

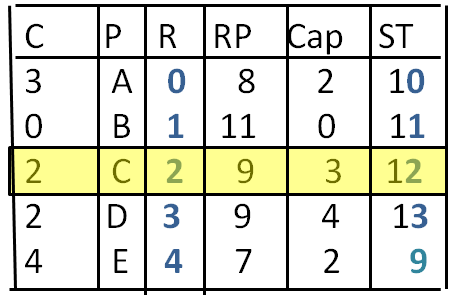
La ST di ciascuno risulta tale che la sua divisione per 5 dia proprio il resto impostosi da ogni prigioniero 10:5 resto 0, 11:5 resto 1, 12:5 resto 2, 13:5 resto 3, 9:5 resto 4.

Ogni prigioniero ha eseguito il suo compito che non era quello di cercare di dare la risposta giusta, ma di coprire, indipendentemente dal SUO risultato, l'eventualità di avere un certo resto. Ogni prigioniero si è imposto un resto diverso, il che vuol dire che uno e uno solo di loro ha dato sicuramente la risposta giusta (i resti possibili erano solo 5, ossia 0, 1, 2, 3 e 4). Nel caso appena trattato è il prigioniero B  a dare la risposta giusta, che li salva tutti. Per lui (e solo per lui) il Cap è uguale a C.

E' abbastanza ovvio intuire perché avere dieci prigionieri sia un gran vantaggio per il calcolo: i multipli di 10 terminano sempre per 0. Il che vuole  dire che il resto finale che deve ottenere ogni prigioniero è proprio la cifra finale della sua ST: 12 ha resto 2, 24 ha resto 4,  31 ha resto 1 e via dicendo...

Concludiamo facendo un esempio proprio per 10 prigionieri, utilizzando la tabella precedente:

Provate pure con numeri di cappelli diversi (magari tutti uguali o tutti diversi tra loro) e vedrete che vi sarà sempre uno e uno soltanto tra i prigionieri a dare la risposta giusta!