Categorie: Matematica Riflessioni
Tags: karatsuba moltiplicazione
Scritto da: Oreste Pautasso
Commenti:5
Per una moltiplicazione in meno
Per una moltiplicazione in meno
Il fluire nitido e spedito di una dimostrazione matematica non rispecchia generalmente il processo mentale che l'ha generata. Come l'acqua di un fiume che scorre placidamente a valle, non racconta nulla delle cascatelle e dei vortici del suo percorso iniziale.
Perché le idee difficilmente nascono secondo un preciso percorso lineare, come quello descritto nella loro “dimostrazione ufficiale”. Le idee emergono per associazione, per riconoscimento di strutture e analogie, per improvvise illuminanti rivelazioni che hanno loro percorsi sotterranei nel subconscio.
Se fosse possibile registrare il pensiero, potremmo vedere attraverso quali spiraleggianti sentieri si arriva al nocciolo del problema e alla sua soluzione.
Mentre l'applicazione di regole note per risolvere un problema dai contorni ben definiti non è altro che una operazione di routine, la ricerca di nuove regole che risolvano più efficacemente quel problema richiede un distacco dall'ovvio e una esplorazione di visioni originali che svelino le possibili alternative. Non si tratta quindi di un processo ordinato, di una procedura rigida, anche se, a cose fatte, la sua enunciazione e la sua dimostrazione saranno costituite da una precisa concatenazione di passi logici.

Prendiamo la moltiplicazione, quella che abbiamo imparato nei primissimi anni di scuola.
La classica moltiplicazione in colonna con i due moltiplicandi, sotto i quali sfilano i risultati parziali, ordinatamente accodati ed allineati in attesa della somma finale che darà il risultato.
La moltiplicazione è la “via breve” che sostituisce un numero di somme che in certi casi potrebbe essere sterminato.
Niente da dimostrare, basta eseguire meticolosamente la procedura.
Ma se dobbiamo moltiplicare numeri veramente grandi, come avviene nella crittografia dei dati, che protegge le nostre comunicazioni e le nostre carte di credito, usando numeri primi di centinaia di cifre moltiplicati tra loro, allora la “via breve” potrebbe non essere abbastanza breve.
Eseguire una moltiplicazione è molto più impegnativo (per noi ma anche per un computer) quanto più grande è il numero delle cifre di moltiplicatore e moltiplicando. Quindi meno moltiplicazioni sono in gioco, minore è la complessità del calcolo ed il tempo necessario per la sua esecuzione.
Vediamo più in dettaglio quante moltiplicazioni elementari sono richieste per moltiplicare due numeri tra loro: ciascuna cifra del moltiplicando va moltiplicata per ciascuna cifra del moltiplicatore.
Quindi se moltiplico due numeri di 4 cifre dovrò eseguire 16 moltiplicazioni elementari.
Se potessi in qualche modo ridurre questo numero otterrei il risultato più velocemente.
Una prima idea è di considerare ciascun numero di 4 cifre come la somma di due numeri; uno più grande per le centinaia, l'altro più piccolo che completa il numero.
Ad esempio 1234 = 1200 + 34 e, altro esempio: 5678 = 5600 + 78
Diamo un nome a questi valori con opportune lettere:
1200 = a* 10^2 34 = b 5600 = c*10^2 78 = d.
Adesso la nostra moltiplicazione la posso indicare in questo modo:
(a *10 ^2 + b ) * (c*10^2 + d) = ac*10^4 + (ad+bc) 10^2 + bd
Tuttavia anche con questa diversa notazione le moltiplicazioni restano sempre 16 perché:
a*c richiede 4 moltiplicazioni elementari , e lo stesso vale per ad , bc e bd.
Occorre intervenire in un modo “innovativo”, osservando specialmente quel binomio ad + bc con la determinazione di trasformare quelle due moltiplicazioni in un sola.
Facciamo una parentesi “geometrica” per vedere meglio quali interventi siano possibili.
 |
I due rettangoli di area a*d e b*c sono una parte del rettangolo grande (a+b)*(c+d) e la loro somma è proprio il valore che ci interessa.
Gli altri due rettangoli hanno area rispettivamente a*c e b*d. Ma guarda che combinazione... quei due prodotti li conosciamo già: ac è il coefficiente del termine più grande (10^4) e bd è il coefficiente del termine più piccolo (10^0). |
Quindi, calcolando l'area complessiva (a+b)*( c+d) e sottraendo ac e bd ( i cui risultati sono già disponibili), otterrei esattamente il valore (ad + bc) coefficiente del termine intermedio (10^2).
La differenza tra i due calcoli non è nel risultato ma nel fatto che, riutilizzando i risultati delle due moltiplicazioni già eseguite (ossia a*c e b*d, che hanno già richiesto 8 moltiplicazioni elementari) posso ridurre il numero di moltiplicazioni restanti da due (ad e bc) a una sola (a+b)*(c+d) previa l'esecuzione delle somme in parentesi.
Così aggiungerò solo 4 moltiplicazioni elementari invece di 8.
Il totale delle moltiplicazioni elementari passa quindi da 16 a 12, come desideravamo.
La soluzione del problema di abbattere il numero di moltiplicazioni necessarie con il metodo classico è stata trovata nel 1962 dal matematico russo Karatsuba. Il suo algoritmo è poi stato migliorato in modo significativo da altri matematici che hanno ottenuto progressivamente negli anni successive drammatiche riduzioni della complessità di calcolo.
Ma tornando al punto, possiamo dire che Karatsuba ha formulato la sua idea nel modo in cui è descritta ufficialmente? Oppure è più probabile che abbia seguito una intuizione (come quella che ho raffigurato geometricamente) per arrivare alla sua ottimizzazione dell'algoritmo?
Questo algoritmo è descritto in rete da molti autori, in modi leggermente diversi che tuttavia non ricostruiscono il possibile percorso logico con cui Karatsuba è arrivato a formularlo.
Non fanno alcun riferimento, ad esempio, allo schema geometrico che ho proposto, ma introducono ex abrupto il passaggio risolutivo.
La mia personale convinzione è che Karatsuba concentrandosi sull'idea vincente di capitalizzare sui risultati già ottenuti, riciclandoli nel calcolo mancante, abbia avuto in mente qualcosa di simile al semplice schema dei rettangoli o qualche altra analogia che lo ha guidato verso la soluzione.
Cuneo, agosto 2023






5 commenti
Ma questi matematici successivi a Karatsuba dalle nostre 12 operazioni elementari a quante di meno sono riusciti ora ad arrivare?
La convenienza degli algoritmi di moltiplicazione rispetto a quelli tradizionali ( in termini di tempo di esecuzione del calcolo computerizzato) è significativa per numeri di grandi dimensioni.
Tipicamente l'algoritmo di Karatsuba ha come punto di riferimento numeri superiori a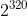 che corrisponde a
che corrisponde a 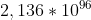
La moltiplicazione Toom-Cook è la generalizzazione più veloce dell'algoritmo di Karatsuba e risale al lontano 1963. Toom e Cook migliorarono questo metodo dividendo i numeri in r blocchi (invece di 2 come aveva fatto Karatsuba).
Ad esempio in una moltiplicazione di due numeri di 8 cifre ciascuno, il calcolo completo richiede solo 27 prodotti a due cifre invece dei 64 del metodo normalmente usato.
Questo metodo, fastidioso a mano, rivela tutta la sua potenza nella esecuzione da parte di una macchina.
Per numeri di 1.000 cifre le operazioni sono nell'ordine di 50.000 invece di 1.000 000.
L'algoritmo di Schönhage-Strassen è un algoritmo di moltiplicazione rapido per grandi numeri interi, sviluppato da Arnold Schönhage e Volker Strassen nel 1971.
L'algoritmo di Schönhage-Strassen era asintoticamente il più veloce metodo di moltiplicazione conosciuto tra il 1971 ed il 2007, finché non è stato annunciato l'algoritmo di Fürer che ha complessità asintotica minore, però al momento risulta vantaggioso solo per numeri astronomicamente grandi e non è utilizzato praticamente.
In pratica, l'algoritmo di Schönhage-Strassen è più veloce di metodi vecchi come quello di Karatsuba e di Toom-Cook per i numeri da 2^215 a 2^217 (10.000 a 40.000 cifre decimali) ed basato sull'uso della Fast Fourier Transfomation (trasformata veloce di Fourier).
Non posso esimermi a questo punto dal segnalare i fondamentali articoli di Enzo sulla Analisi di Fourier che tutti dovrebbero leggere.
Attenzione a non confondere Fourier (che ci ha lasciato nel 1830) con il nostro contemporaneo Fürer
Anche tu vedo che parli di numeri astronomici. Mi fai venire in mente una battuta di Feynman che parlando del numero di stelle in una galassia e del numero di galassie commenta: 2 mila miliardi sono ormai il debito pubblico di una nazione; ormai bisognerebbe chiamarli numeri economici!
Sono d'accordo, economici, però li considero piuttosto "costosi" ...