Nel precedente articolo intitolato “il pavone planò e cosa vide?” avevo promesso che avrei ripreso l'argomento utilizzando un quadro prospettico in posizione mobile (a distanza costante dall'osservatore).  Questo accorgimento permette di risolvere il problema di rappresentare, in prospettiva centrale, la visione durante la planata in base a semplici relazioni che legano le variabili.

Come disegnare l'immagine prospettica senza riga né compasso

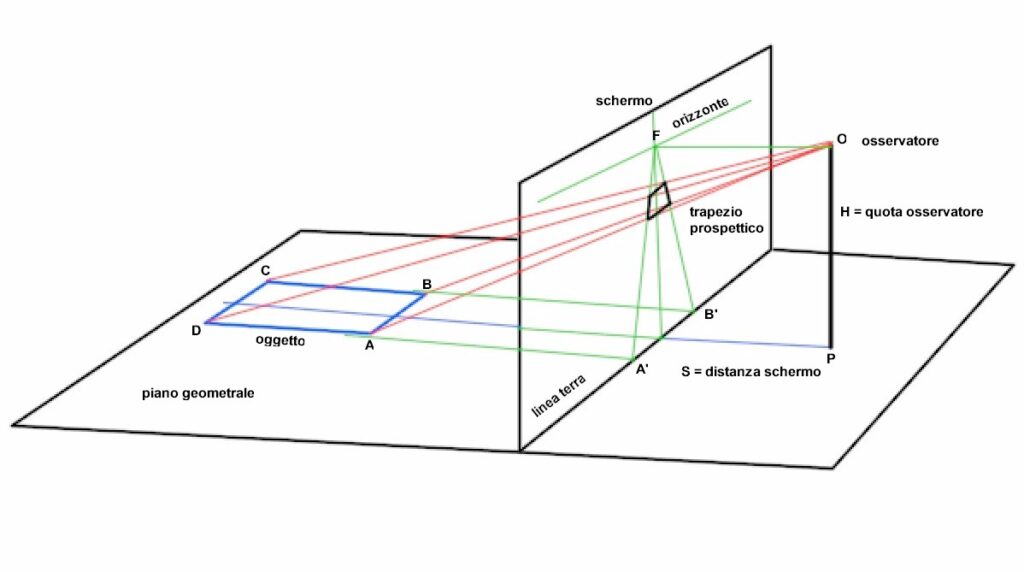
In questa prima figura è rappresentata la visione che ha un osservatore O dell'oggetto (rettangolo blu) disegnato sul piano orizzontale, guardandolo attraverso lo schermo posizionato in verticale ad una certa distanza.

Data la simmetria del rettangolo e la posizione dell'osservatore, sulla linea mediana, l'immagine che si formerà sullo schermo avrà la forma di un trapezio isoscele.

I lati inclinati del trapezio si trovano sulle rette prospettiche che si intersecano nel punto di fuga F, posto sull'orizzonte frontalmente all'osservatore.

Intendiamo esprimere le misure di base maggiore e minore e le quote a cui sono rispettivamente posizionate, in funzione delle posizioni dell'osservatore O e dello schermo S, nonché delle misure dei lati del rettangolo ABCD.

La collocazione del punto P rispetto allo schermo non deve introdurre aberrazioni prospettiche, ossia l'angolo sotto cui da P si vedono i punti A e B non deve superare un certo limite. Poniamo quindi che l'angolo APB sia di 90°, ossia che la distanza di P dal piano dello schermo sia AB/2.

Calcolo della misura delle basi del trapezio

Esaminiamo ora nella seconda figura due viste “dall'alto” che mettono in evidenza le relazioni tra le misure dei segmenti AB e CD e le corrispondenti misure delle loro immagini sullo schermo.

A sinistra vediamo la percezione dell'osservatore della distanza A'B' sullo schermo a rappresentare il segmento AB.

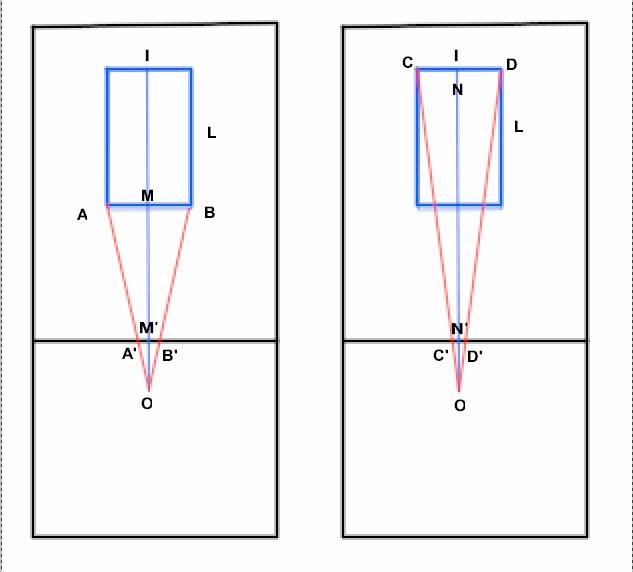
Dalla similitudine dei triangoli ABO e A'B'O deduciamo che:

A'B' : M'O = AB: MO da cui A'B' = M'O * AB/MO

M'O è la distanza tra osservatore e schermo, nella ipotesi che abbiamo posto

questa distanza vale AB/2 = l/2 ( ossia larghezza rettangolo/2)

AB è la larghezza l del rettangolo e MO la distanza (che chiamiamo d ) tra l'osservatore ed il lato AB.

Pertanto A'B' = l/2 * l / d = l² / 2d misura della base maggiore del trapezio

Con lo stesso ragionamento, applicato ai triangoli simili CDO e C'D'O, nella figura di destra, troviamo la relazione che lega CD a C'D'

C'D' : N'O = CD: NO da cui C'D' = N'O * CD/NO

N'O è la distanza tra osservatore e schermo, nella ipotesi che abbiamo posto

questa distanza vale ( AB/2 = l/2 (larghezza rettangolo/2)

CD è la larghezza l del rettangolo mentre L è la sua lunghezza. La distanza NO tra l'osservatore ed il lato CD vale quindi d + L.

Pertanto C'D' = l/2 * l / (d+L) = l² / 2(d+ L) misura della base minore del trapezio

Calcolo delle quote delle basi del trapezio

Passiamo ad esaminare la terza figura, costituita da due viste laterali, che ci consentiranno di stabilire le quote a cui sono posizionate le due basi.

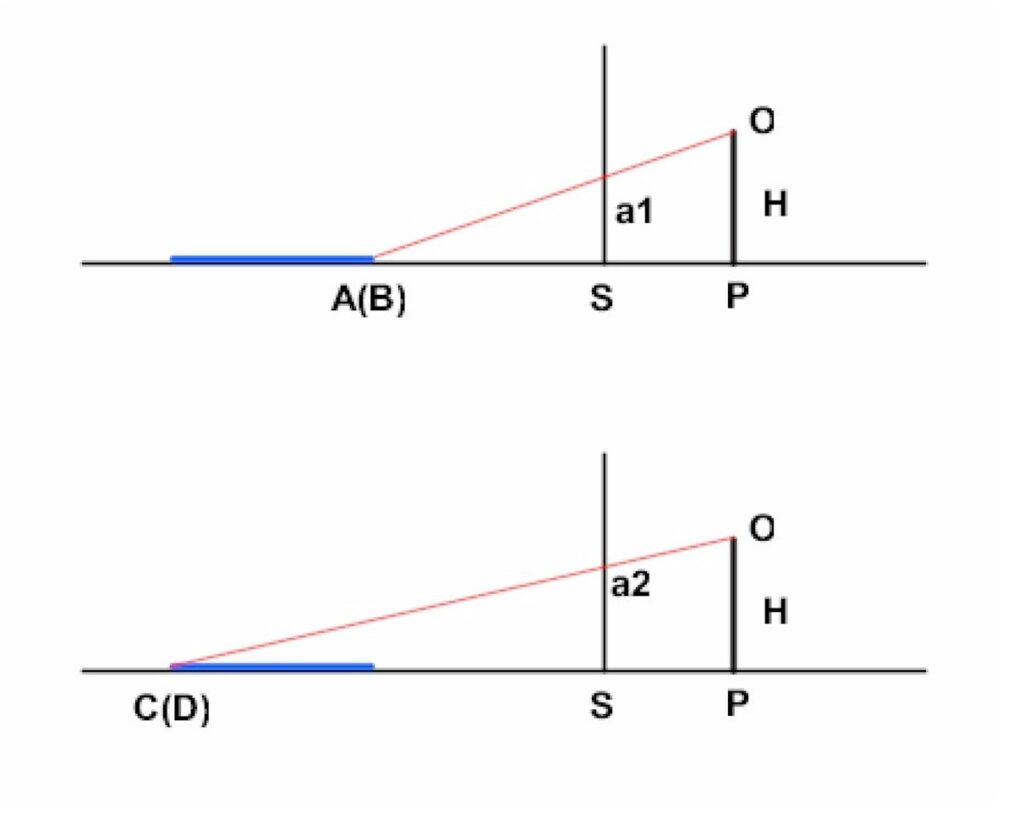
L'immagine superiore mostra come i punti del segmento AB sono visti dall'osservatore ad una quota a1.

Dalla similitudine tra i triangoli AOP e Aa2S possiamo scrivere:

a1 S : AS = OP: AP

Chiamiamo a1 S semplicemente a1 (quota di posizionamento della base maggiore) e indichiamo con H la quota OP dell'osservatore. Inoltre osserviamo che AP = d, distanza osservatore da AB e che SP = l/2 ,come ipotizzato.

L'espressione diventa allora: a1 = (d-l/2) * H/d quota della base maggiore

In modo del tutto analogo calcoliamo la quota a cui va collocata la base minore.

L'immagine inferiore mostra come i punti del segmento CD sono visti dall'osservatore ad una quota a2.

Dalla similitudine tra i triangoli COP e Ca2S possiamo scrivere:

a2 S : CS = OP: CP

Chiamiamo a2 S semplicemente a2 (quota di posizionamento della base minore) e indichiamo con H la quota OP dell'osservatore. Inoltre osserviamo che CP = d + L, distanza osservatore da CD e che SP = l/2 ,come ipotizzato.

L'espressione diventa allora: a2 = (d+L - l/2) * H/(d+L) quota della base minore

Riassumendo

base maggiore l² / 2d alla quota (d-l/2) * H/d

base minore l² / 2(d+ L) alla quota (d+L - l/2) * H/(d+L)

Queste quattro semplici espressioni ci consentono di disegnare il trapezio nelle sue esatte dimensioni e posizione sul quadro prospettico.

E' anche possibile utilizzarle per generare in una stessa figura più trapezi rappresentativi delle immagini viste da un osservatore in movimento, per il quale si modificano anche contemporaneamente quota e distanza.

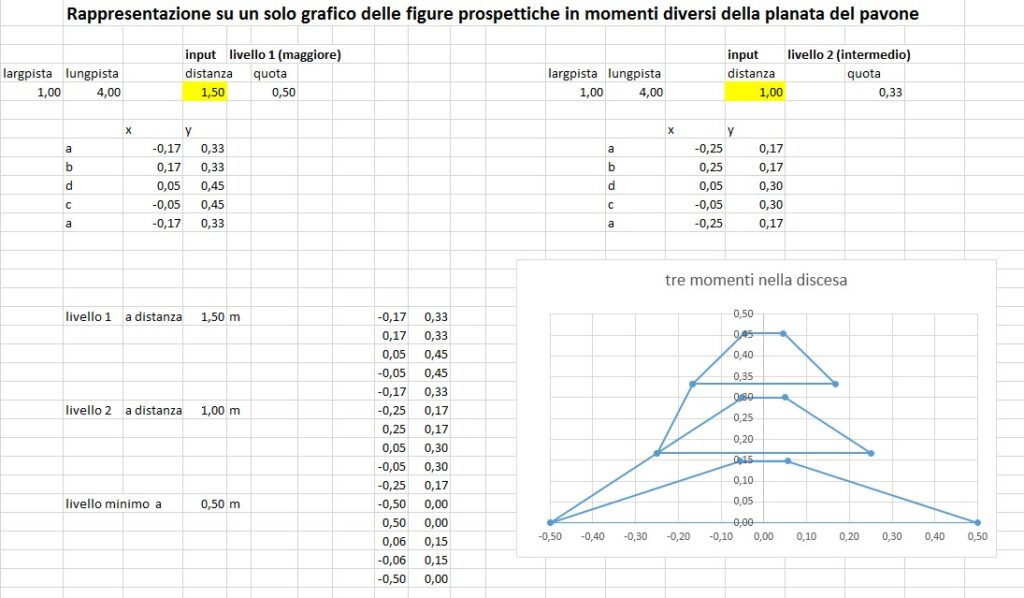
La figura che segue è proprio la trasposizione in un foglio excel di questo calcolo con il relativo grafico.

L'esempio è relativo alla planata del pavone descritta nel precedente articolo.