Categorie: Matematica
Tags: geometria quiz soluzione triangoli isosceli
Scritto da: Vincenzo Zappalà
Commenti:14
Soluzione e discussione sul quiz più difficile dei facili, ovvero: isoscelando, isoscelando...**
Il nostro Maurizio mi ha avvertito che lo stesso quiz era già stato proposto (e risolto in vari modi) dal Club dei Maghi (QUI). Ne consegue che la soluzione la potete trovare in quell'articolo. Nel frattempo sia Maurizio che Andy hanno anche presentato nei commenti due ulteriori metodi di soluzione e invito entrambi a completare la loro dimostrazione.
Tuttavia, nello svolgimento del quiz è stata usata anche la similitudine dei triangoli, un concetto che non avevo menzionato nell'introduzione allo stesso ("la somma degli angoli interni di un triangolo vale 180° e che un triangolo che abbia due angoli uguali è un triangolo isoscele")
Mi sono allora imposto di provare ad arrivare alla conclusione solo con quanto citato in grassetto (niente similitudine). Come prima tappa risolverò un problema molto simile utilizzando solo triangoli isosceli e, ovviamente, la somma degli angoli interni. In poche parole... isoscelando, isoscelando giungeremo alla meta.
Il triangolo di partenza è sempre lo stesso: un triangolo isoscele di angoli 80°, 80° e 20°. Quello che cambia sono le linee che tracciamo dai vertici della base, come mostra la Fig. 1.
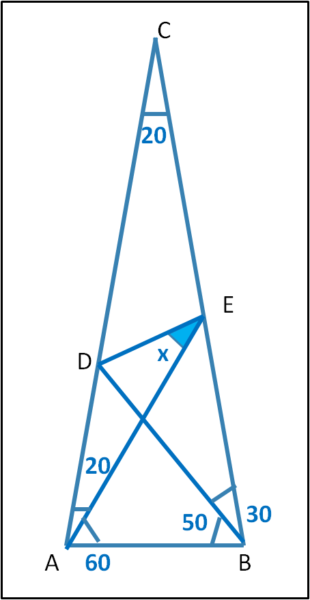
Iniziamo coll'indicare alcuni angoli che si derivano immediatamente attraverso la somma degli angoli interni e le conseguenze che comportano:
ADB = 180 - 50 – 80 = 50°
Da cui segue subito:
Il triangolo ADB è isoscele
AD = AB (vedi Fig. 2)
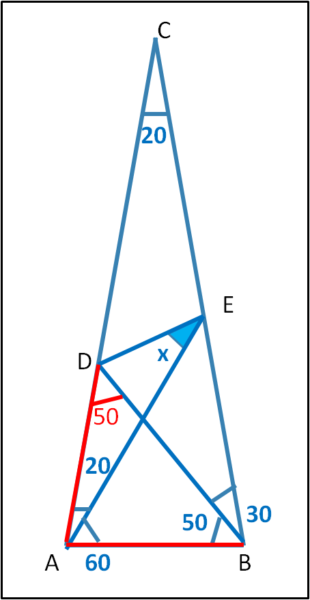
In Fig. 3, tracciamo il segmento AM in modo tale che
BAM = 20°
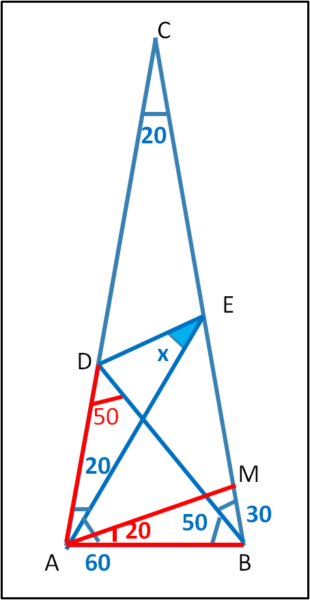
Ne segue che:
AMB = 80°
Il triangolo AMB è isoscele
AM = AB
Consideriamo il triangolo AME (Fig. 4)
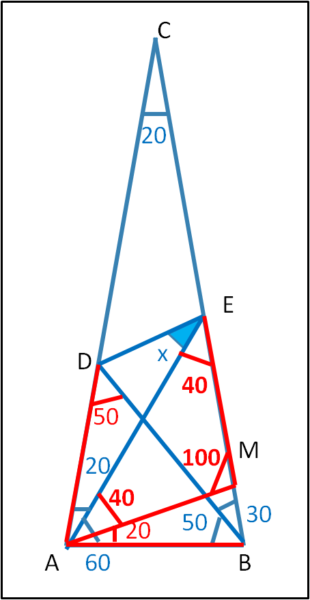
AME = 180 - 80 = 100
EAM = 60 - 20 = 40°
Ne segue che:
AEM = 180 - 100 - 40 = 40°
Il triangolo AEM è isoscele
da cui:
MA = ME
Consideriamo il triangolo DAM (Fig. 5)
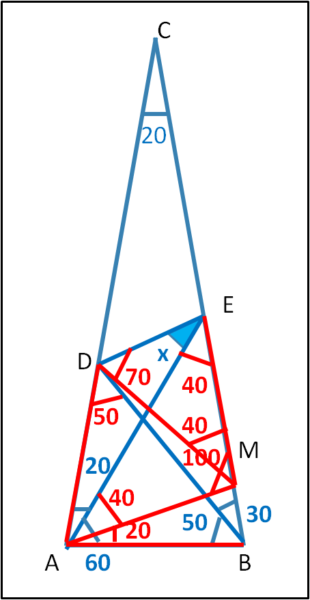
MA = DA
Il che implica che il triangolo DAM è isoscele
Inoltre:
DAM = 40 + 20 = 60°
La somma di ADM e AMD deve essere 180 - 60 = 120°
ADM + AMD = 120°
ADM = AMD = 60°
Il triangolo DAM è equilatero
MA = DM
Passiamo al triangolo MDE.
Ricordando che:
MA = ME
Abbiamo:
ME = DM
Il triangolo MDE è isoscele, ossia:
MDE = DEM
Inoltre:
MDE + DEM = 180 - 40 = 140°
DEM = 140/2 = 70°
per cui:
x = DEM - AEM
x = 70 - 40 = 30°
E questo caso è risolto senza similitudine!
Vediamo in Fig. 6 cosa abbiamo imparato da questa soluzione, con una piccola aggiunta (tanto per continuare a isoscelare ...):
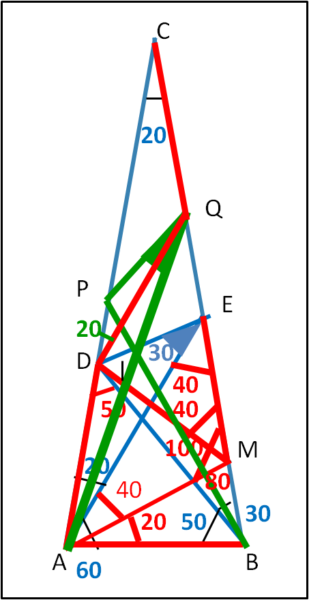
Tracciamo il segmento DQ, tale da formare un angolo di 20° con CA. Ne segue che
DQ = CQ = DA = DM = EM = AM = AB
con tutti gli angoli corrispondenti (aiuto non ho più spazio!).
Tracciando PB, QA e PQ ricadiamo nel quiz originale (linee verdi), ma con molte relazioni già fatte nostre.
Sono convinto che in breve si possa ricavare PQA (senza similitudini) che è la domanda del quiz originario. Che ne dite? Volete darmi una mano?






14 commenti
Per prima cosa completo, come richiesto, il ragionamento presentato nel commento al quiz il 9/11/23 alle ore 19.00.
La prima parte ( di incoraggiamento) che riporto qui era questa...
la seconda parte, ossia la conclusione è questa:
Oppure, compattando tutto in una sola figura e con una conclusione alternativa, ma equivalente...
In questo secondo commento desidero esprimere un sentito ringraziamento a Colui che ha inventato le similitudini dei triangoli.
Dopo questo doveroso tributo veniamo alla soluzione isoscelosa pura.
Caro Enzo, questa soluzione è molto avvincente, quasi ipnotica, e sono tentato di proseguire sulla strada che indichi dei triangoli isosceli ( per la verità c'è anche un triangolo equilatero che è più isoscele degli altri). Prima però mi devo rileggere per bene i vari passaggi.
E se questo sistema di costruire triangoli isosceli a catena funzionasse solo in questo caso perché esiste in partenza il triangolo isoscele ABD (80 50 50 )?
Non credo Mau... posso sempre costruirmi i triangoli che voglio...
Allora si potrebbe partire costruendo inizialmente quel triangolo isoscele che ha i due angoli da 50° (ABD e BDA).
Proseguendo con la tua costruzione si arriva al segmento DE di lunghezza uguale ad AB.
Andando avanti come indicato nella figura sotto si dovrebbe trovare X.
C'è qualcosa che non va...
Innanzitutto, potresti usare le mie lettere per non creare maggiore confusione.
Fino a un certo punto va bene, ma poi scrivi
HEF = 10
e questo NON è vero.
Probabilmente, potremmo collegare la tua ultima figura delle 19:27 a quanto stabilito finora.
Mi sembra che stiamo esagerando... in fondo, l'equazione che va bene per tutti i casi l'avevate già scritta.
E' vero, ho scritto HEF = 10 invece di HEK = 10.
Comunque adesso rifaccio la figura con le stesse lettere che hai usato tu.
Forse stiamo esagerando, come dici, ma mi pare che siamo vicini al risultato.
Prima la figura conclusiva della tua dimostrazione_
Poi, usando le tue stesse lettere (ne ho aggiunta altre per proseguire) la figura conclusiva:
PERFETTO Mau! Adesso sì che ci siamo... però, che fatica essere facili
Vero.
Ma, come diceva Churchill,
" Combatteremo sulle spiagge... non ci arrenderemo mai "
Mi riferisco alle lettere dell’ultima figura.
Traccio la parallela da P ad AB. Si determinano due triangoli equilateri.
Il cerchio per ABQ, essendo AKB =60 = 2AQB = 2*30, ha centro in K.
Perciò QK=KB, da cui KQB=20 che conduce a QK//AC.
Quindi QKF=20 e quindi PF=FK=QF. Per cui PQF =(180-80)/2=50.
A questo bisogan togliere KQF=20 e KQA=10.
Resta 20
caro sprmnt21,
è un piacere vedere la tua passione (e capacità) per la soluzione dei problemi geometrici. Si vede che ti piace la geometria classica!!
Sì una (tanto) vecchia passione che si è risvegliata per caso.
Passando per caso sul vostro sito.
ma adesso non devi più lasciarci...