Andy e Fabry hanno risolto il quiz in vari modi... Io aggiungo una soluzione che fa uso della sola geometria e sfrutta un semplicissimo teorema poco conosciuto, quello di Viviani. Molto probabilmente, esso permette anche di essere sicuri di avere generato "a caso" i tre pezzi di segmento.

Innanzitutto scriviamo le condizioni affinché i tre pezzi del segmento possano formare un triangolo. Per visualizzare meglio il problema disegniamo la Fig. 1 dove sono raffigurati due casi.

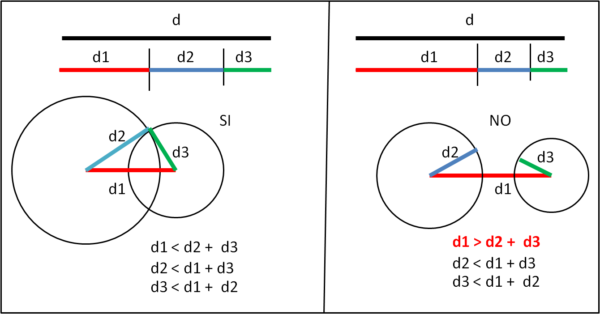
A sinistra abbiamo un triangolo e possiamo notare che la somma di due pezzi è sempre maggiore del terzo pezzo. A destra, non si verificano tutte tre le condizione, in quanto, almeno in un caso, la somma di due pezzi  è minore del terzo. Scriviamo quindi le condizioni affinché i tre pezzi d1, d2 e d3 POSSANO formare un triangolo. Ribadiamo che devono essere soddisfatte TUTTE e tre le condizioni.

d1 < d2 + d3

d2 < d1 + d3

d3 < d1 + d2

Possiamo trasformarle in tre relazioni ancora più semplici e utili.

d1 + d1 < d1 + d2 + d3 = d

d1 < d/2

e, analogamente,

d2 < d/2

d3 < d/2                 .... (1)

In altre parole, la condizione per potere ottenere un triangolo da tre pezzi qualsiasi, impongono che ogni pezzo sia minore della metà del segmento originario. Condizione, questa, che si poteva anche dedurre immediatamente.

Disegniamo, adesso, un triangolo equilatero e prendiamo un punto qualsiasi P al suo interno. Tracciamo dal punto P le tre perpendicolari ai tre lati (h1, h2 e h3) in Fig. 2.

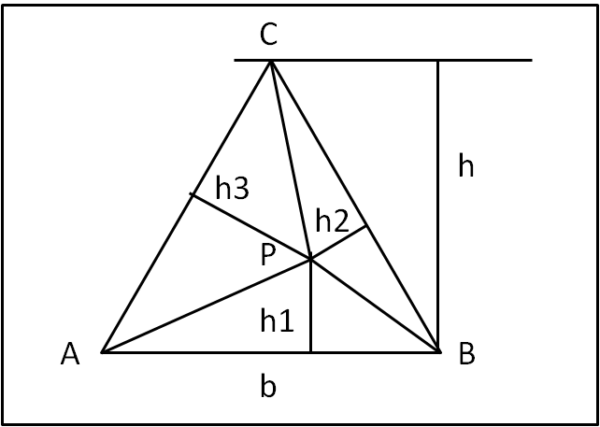
Ed ecco saltar fuori il teorema di Viviani che dice che la somma di queste tre perpendicolari  è una costante, uguale all'altezza h del triangolo. Ossia:

h1 + h2 + h3 = h

Sostituendo  h con d, il punto P permette di descrivere TUTTE le combinazioni possibili di d1, d2 e d3, in modo,  che la loro somma sia sempre uguale al segmento d.

A questo punto ricordiamoci le tre condizioni (1) per poter avere un triangolo con d1, d2 e d3.  d1 deve essere minore di d/2 e così gli altri due pezzi d2 e d3. Tracciamo questi limiti nella parte alta di Fig. 3.

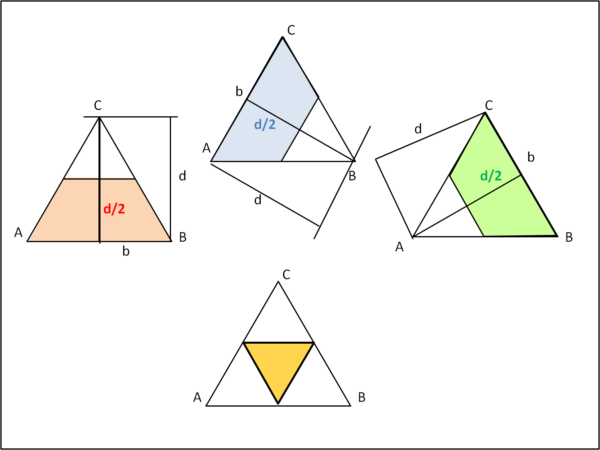
Noi vogliamo solo la parte che verifica tutte e tre le condizioni ed essa è il triangolo di colore arancione (parte bassa della figura). Essendo il triangolo equilatero, esso è diviso in 4 triangoli  uguali di cui la parte che soddisfa tutte e tre le condizioni per poter formare un triangolo è proprio uno di questi.  Per poter avere la probabilità che il nostro segmento originale sia tagliato in modo da poter formare un triangolo, dobbiamo fare il rapporto tra l'area del triangolo arancione  e l'area dell'intero triangolo che, come sappiamo, rappresenta tutte le possibili combinazioni dei tre pezzi.

Come già detto il triangolo arancione ha un'area che è 1/4 di quella totale e quindi la probabilità di avere un triangolo dal taglio di tre pezzi qualsiasi è 1/4.

Dimostrazione del teorema di Viviani.

La dimostrazione è proprio banale e utilizza la Fig. 2. L'area totale del triangolo è data base per altezza diviso due, ossia:

A = b h/2

Ma l'area del triangolo è anche uguale alla somma dei tre triangoli, che hanno per base la stessa base (il lato del triangolo) e per altezza la perpendicolare dal punto P ai tre lati (h1, h2, h3). Abbiamo, perciò:

A = A1 + A2 + A3

1/2 bh = 1/2 bh1 + 1/2 bh2 + 1/2 bh3 = 1/2 b(h1 + h2 + h3)

Ossia:

h = h1 + h2 + h3

c.v.d.