Doppia riflessione

Riprendiamo, allora, la doppia riflessione sulla lastra di vetro e vediamo di sezionarla in vari passi, adottando la moltiplicazione appena descritta. Ancora una volta, ricordo che stiamo semplificando la situazione considerando solo la traiettoria di massima probabilità, senza tener conto della dispersione della luce. In questo caso, siamo interessati a vedere come la luce della sorgente arriva ad uno stesso rilevatore, percorrendo due strade alternative. Alla fine, quindi, si dovranno, comunque, sommare le probabilità ottenute attraverso le due riflessioni.

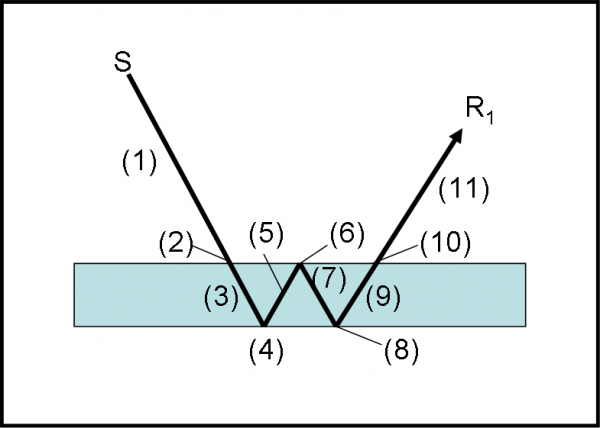
La prima strada è esattamente uguale a quella descritta nella riflessione semplice. Non la ripetiamo di certo, a parte ricordare il risultato: ampiezza di probabilità uguale a 0.2. Dividiamo in vari passi, invece, la riflessione che avviene nella seconda superficie. Ne abbiamo considerati sette e li rappresentiamo in Fig. 38  In particolare: (1) tragitto dalla sorgente al vetro; (2) passaggio da aria a vetro; (3) tragitto dentro al vetro da una superficie all’altra; (4) riflessione nella superficie posteriore; (5) nuovamente. il tragitto dentro al vetro, eseguito al contrario; (6) passaggio da vetro ad aria; (7) tragitto dal vetro al rivelatore.

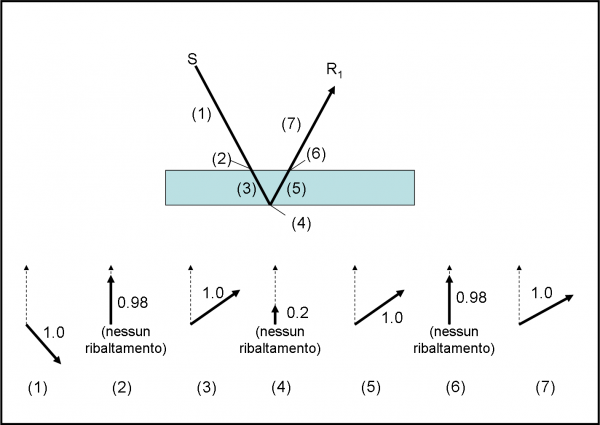
Sappiamo già bene che cosa succede per quasi tutti i passi. Dobbiamo solo aggiungere che la riflessione all’interno del vetro non comporta nessun cambiamento di verso alla freccia. Descriviamo, allora, punto per punto cosa succede. Tra sorgente e vetro non vi è, ovviamente, nessun accorciamento. Il passaggio da aria a vetro comporta, come già sappiamo, un accorciamento di 0.98, ma nessuna rotazione. Il tragitto nel vetro lascia tutto inalterato, tranne la rotazione della lancetta, mentre la riflessione nel vetro origina un accorciamento della freccia pari a 0.2, ma nessuna rotazione. Il ritorno nel vetro lascia inalterata la lunghezza della freccia e fa ruotare la lancetta della stessa quantità che si era trovata nel viaggio di andata (lo spessore della lastra è quello che è). Tuttavia, di quanto giri la freccia, ci importa relativamente poco, per il momento, dato che dipende dallo spessore della lastra.

Più interessante è calcolare l’ampiezza finale che è data dal prodotto dei vari “accorciamenti”. Esso risulta: 1 x 0.98 x 1 x 0.2 x 1 x 0.98 x 1 = 0. 192, che all’inizio di tutto avevamo già approssimato a 0.2. La combinazione con l’altra freccia di 0.2 (prima riflessione) dà un’ampiezza finale che varia da 0 a 0.4 e, quindi, una probabilità che varia da 0 a 0.16 (dallo 0% al 16%), a seconda dello spessore della lastra e, quindi, della rotazione della lancetta all’interno del vetro.

Riassumendo abbiamo stabilito che:

1) una riflessione aria-aria (prima superficie) riduce la freccia unitaria a 0.2 e causa una rotazione di mezzo giro.

2) una riflessione  vetro-vetro (seconda superficie) riduce la freccia unitaria a 0.2 ma non causa nessuna rotazione.

2) un passaggio aria-vetro o vetro-aria riduce la freccia a 0.98.

Siamo come San Tommaso

A questo punto, poniamoci una domanda che non ci eravamo fatti e che sembrerebbe veramente banale: “Cosa registriamo se poniamo un rivelatore al di sotto della lastra della lamina?”. Il percorso è indicato in Fig. 39. Come fatto precedentemente per la semplice riflessione, stiamo confrontando due strade complementari (arrivano a diversi rivelatori), il cui risultato finale non deve portare a combinazione di frecce, ma all’ovvio fatto che la somma delle probabilità legate alle due possibilità DEVE essere 100%. Il fotone o sceglie una strada oppure l’altra: non c’è altra possibilità, per quanto abbiamo assunto fin dall’inizio della moltiplicazione. In parole veramente  “pratiche”: “Se su R₁ la probabilità è del 6%, ad esempio, su R₂ deve essere per forza 100% - 6% = 94%”.

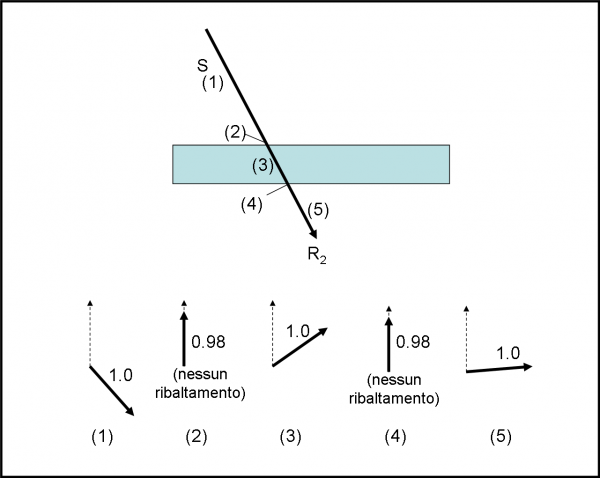
Noi, però, sappiamo che la probabilità di arrivare su R₁ (con due riflessioni) varia tra 0 e 16% e, di conseguenza, la probabilità che la luce arrivi su R₂ deve variare tra il 100% e l’84%.

Tuttavia, la QED ci ha abituato a risultati imprevisti e assurdi e quindi vale la pena calcolare passo per passo la storia della freccia che porta al secondo rivelatore, dato che ormai le regole le conosciamo molto bene. Già il fatto che il percorso sia uno solo comincia a crearci una certa agitazione…

L’evento si scompone in cinque passi: (1) da S alla lastra di vetro; (2) l’attraversamento della superficie  (aria-vetro); (3) tragitto all’interno della lastra di vetro; (4) attraversamento della seconda superficie (vetro-aria); (5) dalla lastra al rivelatore R₂.

Ci vuole poco a calcolare, attraverso il prodotto, l’accorciamento totale della freccia: 1 x 0.98 x 1 x 0.98 x 1 = 0.96

La direzione finale è la rotazione della lancetta senza interruzioni, dalla partenza all’arrivo, dato che non vi sono ribaltamenti.

Più assurdo dell’assurdo

Attenzione, adesso! Come previsto, la QED ci mostra uno dei suoi giochi di prestigio. Indipendentemente dallo spessore della lastra di vetro (che comporta solo diversi valori della probabilità finale di arrivare in R₁), la probabilità di arrivare in R₂ è sempre la stessa (cambia solo il tempo impiegato, ma poco importa dato che NON dobbiamo sommare questa freccia con quella relativa a R₁).

Ripeto ancora il risultato dato che sembra veramente assurdo, benché si parli di QED: l’ampiezza di probabilità, su R₂, è 0.96 e rimane sempre la stessa per qualsiasi spessore. Ciò  comporta una probabilità di giungere in R₂ pari a 0.96² = 0.92. In  altre parole, più terra-terra, su 100 fotoni che partono da S, 92 arrivano SEMPRE su R₂. Su R1, allora, ne dovrebbero arrivare SEMPRE 100 – 92 = 8!

Accidenti, proprio quell’8% che ci saremmo aspettati prima di iniziare a divertirci a combinare le frecce. Eppure sappiamo benissimo, ormai, che la probabilità di giungere su R₁ varia tra 0% e 16%, a seconda dello spessore, passando solo due volte attraverso il valore dell’8%, proprio come ci ha dimostrato la Fig. 3 del primo articolo.

C’è proprio qualcosa che non va. Facciamo un conto da scuola elementare per essere sicuri di non farneticare. Ammettiamo che su R₁ arrivi lo 0% (sappiamo che può benissimo succedere). Adesso sommiamo questo numero a quello trovato su R₂ (che non cambia mai, dato che vi è un solo percorso per arrivarci). Otteniamo 0% + 92% = 92%.... Accidenti, ci siamo persi per strada un 8% di fotoni. Dove sono scappati?

Ma la situazione è ancora più drammatica se , come deve capitare senza alcun dubbio, in R₁ arrivano ben 16 fotoni, ossi se la probabilità è del 16%. La somma delle due probabilità complementari è : 16% + 92% = 108%. Di male in peggio… adesso abbiamo addirittura superato il 100%, come se arrivassero nuovi fotoni dal nulla. Ve bene che la QED è assurda, ma qui si esagera!

Viene da pensare che la freccia o ampiezza di probabilità e il suo modo di calcolarla siano delle grandi fesserie… Eppure ci hanno permesso di calcolare molti eventi legati alla luce, anzi –se crediamo a Feynman- TUTTI.

Un’assurdità dovuta a una visione parziale

Mamma mia, che sciocchi che siamo! Non abbiamo considerate TUTTE le strade che un fotone può compiere per andare da S a R₂. Infatti, ve n’è un’altra che non possiamo certo trascurare ed è rappresentata nella Fig. 40. Essa ci dice che il fotone può riflettersi nuovamente sulla superficie superiore (dalla parte del vetro, però!), tornare indietro, attraversare la seconda superficie e arrivare nuovamente in R₂. Questa volta dobbiamo considerare ben nove passi.

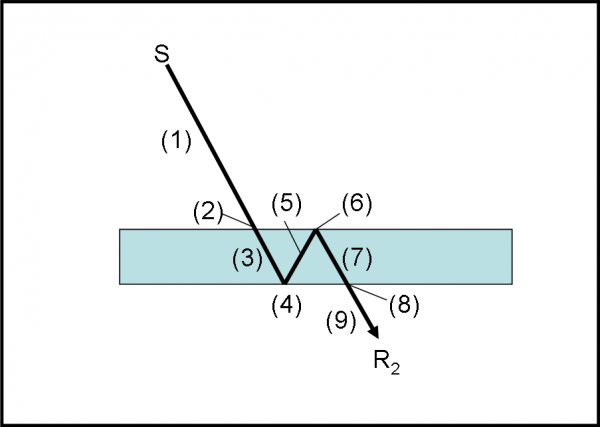
No, non spaventatevi! In fondo è solo questione di accorciamenti e di rotazioni. Quali sono i passi che accorciano la freccia? Sono (2), (4), (6) e (8). Il primo riduce a 0.98, il secondo a 0.2, il terzo a 0.2 e il quarto ancora a 0.98. Moltiplichiamo e otteniamo 0.98 x 0.0.2 x 0.2 x 0.98 = 0.0384, che possiamo approssimare con 0.04. Questa è un’ampiezza di probabilità di un percorso alternativo a quello precedente che  arrivava anch’esso su R₂. Le due frecce o ampiezze di probabilità vanno quindi COMBINATE assieme! Ma la loro combinazione dipende molto dalla direzione delle due frecce da combinare…

Finora non ci eravamo curati della lancetta del cronometro, ma adesso diventa necessario per poter calcolare la vera probabilità che un fotone ha di giungere in R₂. Quanto giri la lancetta nelle due vie alternative legate a R₂ dipende sicuramente dallo spessore della lastra, così come dipendevano dallo spessore le ampiezze che si combinavano in R₁.

Tuttavia, il problema si risolve in modo generale con un ragionamento veramente semplice che è sintetizzato nella Fig. 41.  Permettiamoci, per semplicità di figura, di far ruotare solo la freccia senza curarci della lunghezza, dato che come si accorcia l’abbiamo già calcolato precedentemente.

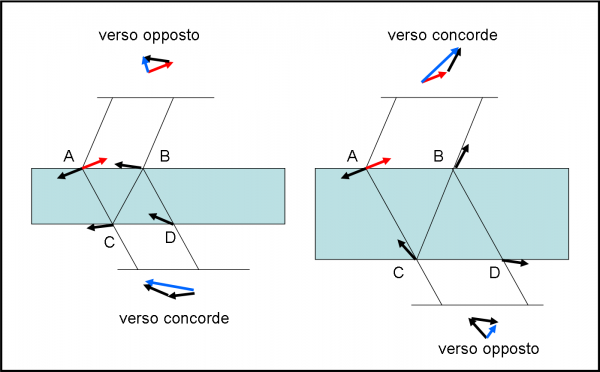
Trascuriamo anche alcuni tragitti che non servono alla soluzione finale. Innanzitutto quello da S ad A che non influenza assolutamente il discorso successivo. Ci dice solo come è diretta la freccia all’inizio della danza dentro alla lastra. Trascuriamo anche  i tragitti da A a R₁ e da B a R₁ così come quelli da C a R₂ e da D a R₂, dato che essi sono uguali, a due a due, per costruzione. La lancetta gira, infatti, dello stesso valore per entrambe le coppie di traiettorie.

Possiamo perciò esaminare la freccia solo nella parte “interna” alla lastra. Domandiamoci: “Quale tragitto, nel vetro, determina la direzione della freccia che si ottiene in B?” Beh… facilissimo: ACB. Non vi è infatti nessuna inversione di direzione in C dato che è riflessione vetro-vetro. Possiamo dire che la direzione della freccia in B può essere diretta comunque rispetto a quella in A, ma questa differenza è solo dovuta allo spessore della lastra.

Nella prima situazione intermedia (parte sinistra della figura), lo spessore è piccolo e la freccia “nera” da A a C e, quindi anche da C a B, ruota solo di 15° (ad esempio). In B quindi si ha una rotazione di 30° rispetto a quella di A. Tuttavia, attenzione! La freccia che non entra nel vetro e viene riflessa direttamente verso R₁ DEVE essere ribaltata rispetto a quella che entra, ossia diventa la freccia “rossa”. In R₁, quindi, qualsiasi sia il tragitto AR₁ = BR1, si devono combinare due frecce che hanno verso quasi opposto (angolo tra loro ben maggiore di 90°) e la cui somma vettoriale si riduce (diventa zero solo se la direzione è esattamente la stessa).

Cosa capita alle frecce che vanno verso R₂? Una è quella in C e l’altra è quella in D. Il tragitto CBD, però, è esattamente uguale ad ACB. Se quest’ultimo ha ruotato la lancetta di 15° + 15° = 30°, lo stesso deve fare anche la freccia che va da C a D. Anche la riflessione in B è vetro-vetro e quindi non comporta inversione di lancetta. Questa volta, la freccia in C si somma vettorialmente alla freccia in D senza subire alcuna inversione: nera è e nera rimane. Ha subito due riflessioni (in C e in B) ma entrambe del tipo vetro-vetro. In R₂, dobbiamo, quindi, combinare due frecce che hanno verso quasi concorde (angolo ben minore di 90°), la cui ampiezza di probabilità finale aumenta. Esattamente il contrario di quanto capita in R₁. Nel caso in cui la direzione è esattamente la stessa, otteniamo la massima lunghezza possibile.

Aumentiamo, adesso, lo spessore (parte destra della figura). Tutto rimane lo stesso, ma la freccia che entra in A gira molto di più prima di arrivare in C. Ad esempio, di 70°. La freccia arriva quindi in B avendo girato di 70° + 70° = 140°. La freccia rossa e quella nera che vanno verso R₁ hanno adesso verso quasi concorde e la loro somma vettoriale aumenta l’ampiezza fino a farla diventare massima se la direzione è la stessa. Dato che il percorso ACB è lo stesso di CBD, anche la freccia che esce in D ruota di 140° rispetto a quella di C. Dato che non hanno subito ribaltamenti esse hanno, questa volta, versi quasi opposti e la freccia finale si riduce, diventano minima quando la direzione è proprio uguale. Attenzione: in questo caso non si annulla l’ampiezza, dato che queste due frecce hanno lunghezza nettamente diversa (0.92 e 0.04) come abbiamo visto precedentemente.

Insomma, quando in R₁ aumenta l’ampiezza, in R₂ si riduce e viceversa. Proprio quello che volevamo!

Tradotto in numeri (ossia, considerando anche le ampiezze e non solo la lancetta), questo procedimento ci porta, nei casi limite, alle seguenti conclusioni:

(a) Se in  R₁ sommiamo due frecce entrambe di 0.2 si ha un’ampiezza finale di 0.4 che porta a una probabilità del 16%. In R₂ avviene, allora, il contrario. A un’ampiezza di 0.96 si deve togliere un’ampiezza di 0.04, ottenendo 0.92. il cui quadrato (ossia la probabilità finale) diventa proprio 0.84, ossia l’84%. Le cose funzionano perfettamente, dato che 16% + 84% = 100%. I cento fotoni partiti da S  non sono aumentati lungo la strada!

(b) Se in R₁ sottraiamo due frecce entrambe di 0.2 si ha un’ampiezza finale di 0 che porta a una probabilità dello 0%. In R₂, avviene il contrario e le frecce si devono sommare. Ossia: 0.96 + 0.04 = 1.00 (ricordiamo sempre che la somma vettoriale in questi casi limite si riduce alla somma aritmetica). La probabilità in R₂ diventa, perciò del 100%. Mi posso permettere di dire che 0% + 100% = 100%. Ancora una volta tutto torna e i famosi fotoni persi per strada non esistono assolutamente. Tutti e 100 arrivano a destinazione.

ESERCIZIO PER I PIU’ ABILI (ma risolvibile da tutti)

Volete vedere se avete capito questa parte un po’ più ardua del solito? Disegnate le frecce nei punti A, B, C e D, nel caso intermedio in cui la probabilità di R₁ è l’8% , verificando che in R₂ si trova una probabilità del 92%. Tutto l’esercizio sta nel disegnare la rotazione giusta della freccia da A a B e, quindi, da C a D… Analogamente, potete disegnare, molto facilmente, anche i casi limite che abbiamo descritto a parole.

Nessuna approssimazione nella QED

Un’ulteriore considerazione estremamente importante. Avrete notato che ogni tanto abbiamo eseguito delle approssimazioni… Un valore di 0.038 l’abbiamo preso uguale a 0.04, ma prima ancora avevamo detto che si poteva approssimare 0.192 con 0.2. Non solo, però…i vari quadrati sono stati spesso tagliati “brutalmente” nelle loro cifre decimali.

Ma come? Una rappresentazione esatta e perfetta come la QED è costretta a eseguire approssimazioni per far tornare le percentuali? Accidenti, siamo mal messi. No, no, cari amici, la QED è l’unica strategia operativa che riesce a determinare perfettamente certe costanti della fisica fino a decimali sempre più lontani dalla virgola. Anzi, può riuscire ad arrivare fino alle dimensioni minime della fisica, se no che “quantistica” sarebbe?

Faccio in fretta a rispondervi. Basta la Fig. 42,  in cui abbiamo aggiunto una nuova riflessione sulla seconda superficie. In R₁ arriva un’ulteriore freccia di ampiezza molto piccola (0.008) che deve combinarsi con quelle precedenti… E che dire se aggiungiamo ancora un’altra riflessione vetro-vetro sulla prima superficie e facciamo uscire il fotone dalla superficie inferiore? Un’altra freccia piccola piccola si combina a quelle precedenti e via dicendo… Insomma, possiamo continuare a far riflettere il fotone dentro al vetro e farlo uscire un po’ sopra e un po’ sotto in modo da ottenere frecce sempre più piccole che si combinano a quelle già trovate sia su R₁ che su  R₂.

ALTRO ESERCIZIO (molto utile)

Potete facilmente, lavorando con calma e pazienza, calcolare la combinazione finale di un percorso come quello appena descritto (e anche quelli successivi). In fondo, basta moltiplicare tra loro gli “accorciamenti” subiti secondo le poche regole imparate finora. Toccherete con mano la continua diminuzione dell’ampiezza delle frecce aggiuntive…  E’ inutile pensare alla lancetta del cronometro: lei continua a percorrere percorsi uguali e il risultato finale non cambia rispetto al caso descritto precedentemente. Le freccette continuano a sommarsi o a sottrarsi a seconda dello spessore della lastra.

Continuando in questa danza ripetitiva, stiamo tranquilli che lo 0.038 diventerà lentamente sempre più uno 0.40 seguito da tanti, tanti zeri! E lo stesso succede per  0.192 che diventa veramente 0.2. Una serie di  trasmissioni e riflessioni che non terminano teoricamente mai. Così come capita nell’arcobaleno: a volte se ne riescono a vedere due, ma, teoricamente, ne potremmo vedere molti di più…

Beh… è stato un articolo abbastanza “duro”  e possiamo fermarci qui. Capisco benissimo che a qualcuno sarà apparso un inutile gioco geometrico e matematico. E, forse, inizierà a pensare che è molto meglio tornare all’ottica geometrica. In fondo, si trovano le stesse cose senza tante frecce e lancette che si accorciano, girano si sommano e si sottraggono. Vi prego di non farlo! Tra non molto, questo assurdo comportamento del fotone si scontrerà con la materia e le cose diventeranno molto più concrete!