In questo terzo capitolo vogliamo fare tre cose:

(1) Introdurre (nuovamente) la relatività galileiana e la trasformazione corrispondente.

(2) Capire bene cosa vuol dire ridurre le dimensioni dello spazio

(3) Rappresentare graficamente lo spazio-tempo galileiano

Il punto (1) lo avevamo già trattato poco tempo fa. Tuttavia, preferisco riportare le nozioni principali per non costringere i lettori a fare avanti e indietro nel sito…

Quello che vogliamo fare è ricavare le formule (ma anche solo i concetti) che legano le coordinate spazio-temporali di uno stesso evento visto in due diversi sistemi di riferimento inerziali. Ciò vuol dire che essi si muovono uno rispetto all’altro con velocità costante. Sappiamo già che le leggi della meccanica non cambiano passando da un sistema all’altro.

E’ meglio togliere subito un paio di dubbi. Ho scritto “meccanica” e non “fisica” perché, in realtà, l’elettromagnetismo non segue la stessa regola. Basti pensare che essa tratta di un qualcosa che viaggia alla velocità della luce (la luce, appunto!) e questo era un problema che non poteva interessare Galileo e Newton (per loro la luce si trasmetteva istantaneamente). Inoltre, non pensiate che la relatività speciale parta da una “base” diversa. Essa si riferisce solo e soltanto a trasformazioni tra sistemi inerziali, proprio come quella galileiana. Il vantaggio sarà quello di poter inserire la parola “fisica” al posto di “meccanica”.  Ma torniamo a Galileo…

La trasformazione galileiana e la somma delle velocità.

Consideriamo due sistemi cartesiani: O(x,y,z,t) e O’(x’,y’,z’,t’). Entrambi si muovono di moto rettilineo uniforme rispetto a un ipotetico riferimento fisso. Possiamo fare due semplici semplificazioni che derivano dal principio d’inerzia, ossia da quanto abbiamo detto precedentemente. Innanzitutto, consideriamo fisso uno dei due sistemi e riferiamo il moto del secondo al primo. In altre parole, consideriamo fisso O e studiamo il movimento di O’ rispetto a lui. Il movimento, inoltre, può avvenire in qualsiasi direzione, ma è possibile scegliere gli assi cartesiani in modo che il movimento avvenga solo lungo l’asse x, coincidente con x’.

Dobbiamo fare, inoltre, un’altra ipotesi di partenza: il tempo t è identico al tempo t’, ossia scorre nello stesso modo in entrambi i sistemi di riferimento. In altre parole, gli orologi in O e O’ segnano sempre la stessa ora. Questa assunzione sembrerebbe derivare da una mancanza di approfondimento da parte di Galileo. Invece, il grande pisano era del tutto conscio del fatto che per essere sicuri che gli esperimenti fatti nei due sistemi di riferimento fossero veramente istantanei si poneva il problema della velocità della luce. Infatti, per dare il via allo sperimentatore che si sarebbe mosso, Galileo doveva fare segnali con una lanterna. Egli fece molti tentativi a distanze crescenti e ne dedusse, ovviamente, che la luce era sicuramente “rapidissima”, concludendo che, qualsiasi possibile valore essa avesse realmente avuto, sarebbe stata del tutto irrilevante ai fini pratici. L’uguaglianza t = t’ non è quindi assolutamente arbitraria, ma basata anch’essa sulla sperimentazione, in accordo col metodo scientifico.

Assumiamo che all’istante t = 0, O’ coincida con O, come rappresentato in Fig. 4. Entrambi gli orologi segnano t = t' = 0 e le coordinate nei due sistemi sono perfettamente identiche.

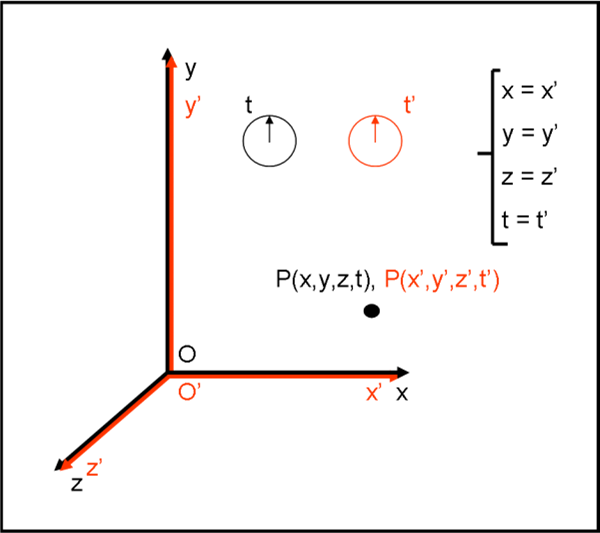
Facciamo adesso muovere O’ con velocità v₀ (posso considerare solo i moduli dato che tutto avviene lungo una sola coordinata spaziale) costante rispetto ad O, come mostra la Fig. 5.

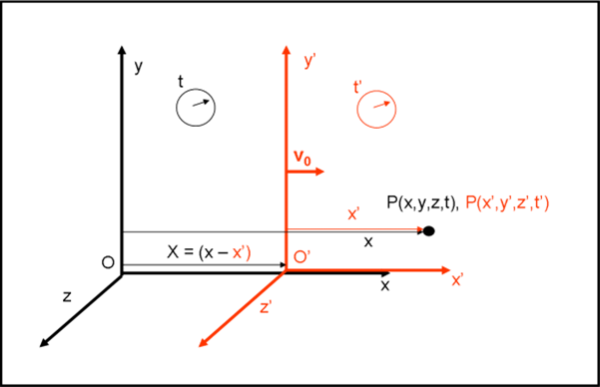
Permettetemi, adesso, di inserire qualche formula, dato che il concetto finale è più che “leggibile” attraverso le figure (così accontento le due schiere di lettori…)

Dopo un  tempo t = t’ (gli orologi segnano lo stesso tempo), l’ascissa del punto O’ rispetto a O sia X. Per definizione di velocità:

v₀ = (X - 0)/(t - 0) = X/t

ossia:

X = v₀ t

Un punto P qualsiasi ha coordinate (x,y,z,t) nel sistema O e coordinate (x’,y’,z’,t’) nel sistema O’.

Per come è stato costruito il secondo sistema, valgono sicuramente le uguaglianze:

y = y’

z= z’

t = t’

Calcoliamo, invece, la relazione tra x’ e x

Dalla figura si ha subito:

x = x’ +OO’ = x’ + X = x’ + v₀ t

Otteniamo, allora:

x = x’ + v₀t

y = y’

z = z’

t = t’                        …. (1)

 

Queste relazioni descrivono la trasformazione galileiana per passare da un sistema di riferimento inerziale a un altro (ottenuto per pura traslazione, ossia attraverso una velocità relativa costante).

Tutto qua. Ripeto, ancora, che mi sono permesso di inserire delle formule, dato che il concetto di sistema di riferimento e di velocità le considero completamente assimilate. Chi avesse dei problemi a questo punto, è inutile che continui. Prima deve assolutamente fare suoi questi concetti. Per semplificare i passaggi successivi, trascuriamo l’asse z (lo potremmo immaginare perfettamente diretto verso di noi). D’altra parte sappiamo che nulla cambia, dato che z’ = z.

Le velocità si sommano

Immaginiamo che il nostro punto P si muova con una certa velocità v’ nel sistema di riferimento di O’. Attenzione: questa velocità può anche non essere COSTANTE. Essa si riferisce a un certo fenomeno fisico che capita nel sistema di O’, ma non inficia assolutamente la definizione di sistema inerziale per O’. Perché un sistema non sia più inerziale è necessario che la velocità tra i due sistemi sia variabile, ma non certo che il fenomeno descritto dal punto P sia legato a una velocità costante.

A questo punto conosciamo la velocità costante v₀ e quella qualsiasi v’. Per semplicità, imponiamo che anche la velocità v’ vada nella stessa direzione di v₀. Come facciamo a determinare la velocità v del punto P rispetto al sistema di riferimento O? Beh… ormai siamo capaci di effettuare le derivate e non ci dobbiamo più spaventare ad applicarle. Sappiamo benissimo che la velocità può essere scritta come ds/dt, ossia come derivata dello spazio rispetto al tempo.

Prendiamo, allora, la prima relazione delle trasformazioni di Galileo (che descrive la relazione tra le ascisse di un punto P qualsiasi):

x = x’ + v₀ t

Per calcolare la velocità del punto P, basta derivare questa espressione rispetto al tempo (la derivata determina, infatti, la variazione istantanea dell’ascissa rispetto al tempo, ossia proprio la velocità):

dx/dt = dx’/dt + d(v₀ t)/dt

il primo termine è proprio la velocità v cercata (la variazione di x nel sistema O). Il secondo termine è la velocità v’ (la variazione di x’ nel sistema O’). Per il terzo termine dobbiamo ricordare la derivata di un prodotto, o -ancora meglio- la derivata del prodotto di una variabile  per una costante.

In un modo o nell’altro, si ricava che la derivata di un prodotto di una costante per una variabile è uguale al  prodotto della costante per la derivata della variabile. In altre parole, la costante esce dall’operazione derivata senza nessun problema (non confondetevi, però: la derivata di una costante è sempre zero). Un’ottima occasione per ripassare la derivata: avete voluto le derivate? Adesso usiamole nella pratica!

In poche parole:

d(v₀ t)/dt = v₀ dt/dt = v₀       (dt/dt è ovviamente uguale a 1).

Alla fine si ottiene la fondamentale relazione:

v = v’ + v₀   …. (2)

Perché è così fondamentale, pur essendo di una semplicità spaventosa oltre che estremamente intuitiva? Perché sarà proprio questa espressione che diventerà insostenibile quando le velocità si avvicineranno a quella della luce. Capire la rivoluzione di Einstein senza aver bene digerito la trasformazione galileiana è un assurdo. Soprattutto perché essa sarà confrontata con la sua trasformazione equivalente valida SEMPRE, quella di Lorentz. Torniamo a noi…

La relazione precedente esprime il principio galileiano (e poi anche newtoniano) di addizione di velocità. Sembra una sciocchezza, ma solo attraverso di lei è stato possibile sviluppare tutta la meccanica classica… Potevamo anche fare a meno di formule e dedurre il risultato direttamente dalla figura precedente assumendo che il punto P si muovesse nel suo sistema di riferimento con velocità v’. bastava sommare segmenti paralleli…

Cosa abbiamo fatto finora? Riassumiamolo a parole.

Abbiamo calcolato come si trasformano le coordinate di un certo evento (il tempo è una coordinata a tutti gli effetti) cambiando il sistema di riferimento. Ci siamo accorti che ciò che cambia è (nelle condizioni favorevoli scelte) solo e soltanto la coordinata x. La nuova x’ è legata alla x attraverso la velocità relativa dei due sistemi di riferimento inerziali (mi raccomando questo aggettivo, non dimentichiamolo mai!).

Con pochi passaggi matematici, abbiamo anche trovato che se un oggetto si muove in un sistema di riferimento con una certa velocità (qualsiasi e anche variabile) e questo sistema di riferimento fa lo stesso (con velocità costante) rispetto a un altro sistema di riferimento, la velocità dell’oggetto rispetto a quest’ultimo è data dalla somma delle due velocità. Un concetto, questo, ovvio e intuitivo nella vita di tutti i giorni.

Pensiamo di essere su un  treno che viaggia velocemente. Lo stiamo, inoltre, attraversando, dalla coda verso la testa, per trovare un posto libero. In poche parole, ci stiamo muovendo con una certa velocità nel sistema di riferimento treno, mentre il sistema treno si muove anch’esso rispetto al sistema di riferimento del capostazione. Come fa il capostazione (fermo sul binario) a sapere la nostra velocità. Deve solo e soltanto sommare la velocità del treno alla nostra che stiamo attraversando il treno. Banale direi… ma solo e soltanto nello spazio-tempo di Galilei.

Notiamo anche bene che finora abbiamo descritto tutto nello spazio, tenendo il tempo da parte. D’ora in poi dobbiamo farlo entrare veramente in gioco come nuova coordinata a tutti gli effetti. Per poter fare ciò è necessario ridurre il numero di coordinate relative allo spazio se no non saremmo in grado di disegnare un bel niente… pensiamo al nostro amico CE…

Riduciamo lo spazio

E’ ora di smettere di passare dal mondo di CE al mondo di CO, CI e SFE e viceversa. Alla fine faremmo solo confusione. E’ anche inutile tirarsi dietro la y e la z nella trasformazione galileiana. L’abbiamo già imposte sempre uguali, attraverso un movimento lungo la sola x. Tagliamo la testa al toro e immaginiamo di vivere in uno spazio S1, dove l’unica coordinata sia la x che potremo poi chiamare anche s (dato che è l’unica).

Non dobbiamo avere paura di farlo. Basta chiedere a CE e lui ormai sa benissimo come fare per passare di nuovo a S2 e poi a S3. Facciamoci aiutare dalla semplicissima Fig. 6 per eseguire questa riduzione di spazio (il tempo lo lasciamo da parte perché è fondamentale conservarlo).

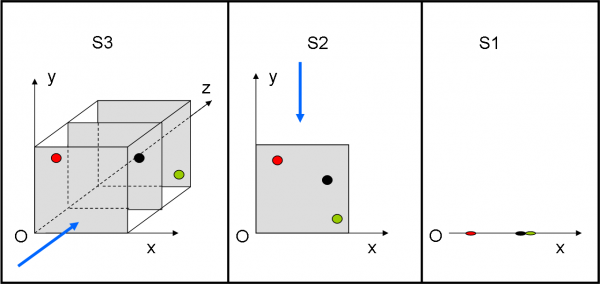
A sinistra, abbiamo il solito spazio tridimensionale (x,y,z). Consideriamo tre diversi piani paralleli al piano (x,y). Il punto rosso ha una certa z (ad esempio, proprio zero), che è diversa da quella nera e da quella verde. Guardiamo la figura secondo la direzione blu. I tre piani contenenti i tre punti si sovrappongono e ciò che vediamo è ora (parte centrale) solo il piano (x,y), con i tre punti ben visibili sistemati con le loro x e y di partenza.

Non ci basta ancora? Bene guardiamo la situazione secondo la linea azzurra parallela all’alle y. Tutto viene proiettato solo e soltanto sull’asse x e la y sparisce, come è riportato nella parte di destra. I punti non hanno più dimensioni, se no il nostro amico CE ci riprenderebbe. Lo spazio a tre dimensioni è stato “concentrato” in uno spazio a una sola dimensione. Poco male, l’importante è sapere cosa abbiamo fatto e che cosa possiamo fare per tornare indietro.

Ogni azione svolta dai punti può svolgersi solo e soltanto sulla retta x, che d’ora in poi possiamo chiamare s. Ogni punto, ha però, dentro di sé anche i valori di y e z, anche se non li rappresentiamo.

A questo punto possiamo facilmente disegnare un evento, ossia aggiungere la coordinata t. Abbiamo, perciò, un piano (s,t) dove possiamo descrivere tutti possibili eventi che avvengono nello spazio-tempo, tenendo presente la trasformazione galileiana  che lega tra loro eventi rappresentati in diversi sistemi di riferimento. Detto in parole ultra semplici, il piano (s,t) rappresenta tutto ciò che esiste, è esistito ed esisterà. Qualsiasi avvenimento può essere rappresentato e i vari eventi possono essere collegati oppure no attraverso linee di universo (non sono più traiettorie, dato che ogni traiettoria spaziale avviene nell’asse s).

Lo spazio-tempo galileiano

Disegniamo innanzitutto, in Fig. 7, il nostro spazio-tempo (piano) segnando le due coordinate s e t. Immaginiamo che il nostro sistema di riferimento sia quello segnato in nero e che sia fermo (si può sempre fare… come ci dicono Galileo & Co.). Attenzione! A questo punto immaginiamo anche di poter vedere tutto lo spazio-tempo da fuori. Questo è un concetto che troppo spesso si dimentica. E’ una cosa teoricamente impossibile, ma il disegno a due dimensione ce lo permette (ricordiamo il caso di CE ed amici) e sfruttiamo questa possibilità.

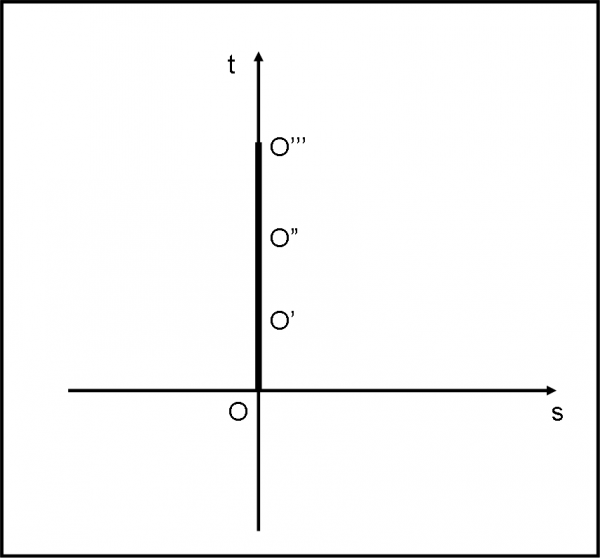
Noi siamo in O. Possiamo stare fermi in questa figura? Assolutamente no. Questa è una caratteristica della coordinata tempo che non possiamo dimenticare. Possiamo anche non muoverci nello spazio s, ma il movimento lungo t non possiamo assolutamente vietarlo o contrastarlo. Il tempo, come già detto, è una brutta “bestia”.

In ogni modo, il punto O rappresenta un evento a cui partecipiamo, anzi è proprio noi. Questo evento è completamente localizzato dalle coordinate s = 0 e t = 0 (potevamo, però, assegnargli valori qualsiasi…). A quali eventi andiamo incontro se continuiamo a non muoverci? Facilissimo, a O’, O”, O’’’, ecc. In altre parole, gli eventi futuri sono proprio localizzati lungo l’asse del tempo. La linea del tempo è la nostra linea di universo.

Attenzione. Stiamo mettendo in pratica quanto detto a parole nel capitolo precedente e che ci ha ricordato anche Einstein con le sue parole. Stiamo, infatti, usando il tempo come una coordinata qualsiasi, dato che possiamo rappresentare contemporaneamente, in una sola figura, sia il passato che il presente che il futuro. Sembra una banalità, ma non lo è, dato che è proprio uno dei requisiti fondamentali per dare al tempo la stessa caratteristica delle altre coordinate (lo spazio, in questo caso semplificato).

Qual è la nostra velocità mentre passiamo da un evento a un altro? E’ esattamente zero (d’altra parte non ci muoviamo). In parole matematiche v = s/t, ma se s = 0, sempre, anche la velocità è uguale a zero, sempre.

Consideriamo, adesso, un nostro amico P (meglio l’evento P) che all’istante t = 0 coincide perfettamente con noi. Lui, però, non ha nessuna voglia di stare fermo e intende muoversi, anche se in modo costante. In altre parole, si muove con velocità costante v_PO (velocità di P rispetto a O), ossia rappresenta un sistema inerziale rispetto a noi. P se ne va quindi per la sua strada e istante dopo istante la sua distanza spaziale rispetto ad O valev_POt_O, dato che per definizione v_PO = s_PO/t_P = s_PO/t_O. Ricordiamo che Galileo assume che t sia lo stesso sia per chi sta fermo che per chi si muove, ossia t_O = t_P.

E’ immediato tracciare la linea di universo di P: essa è una retta inclinata. Inclinata di quanto indica la velocità v_PO. Ricordiamo, infatti, che v_PO è proprio il coefficiente angolare della retta.

Non facciamoci prendere dall’agitazione. Stiamo solo rappresentando il moto rettilineo uniforme nel diagramma spazio-tempo, come già fatto infinite volte per la retta. Nella Fig. 8 la linea di Universo di P non è altri che la retta azzurra.

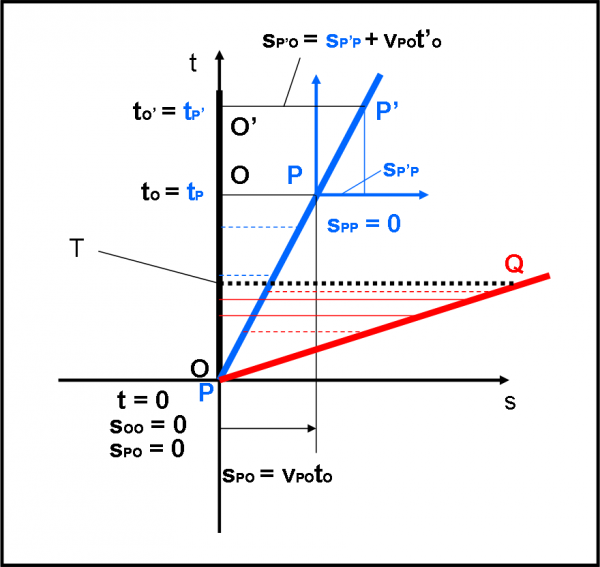
Ripetiamo il tutto con parole che ci colleghino alla trasformazione galileiana. Riscriviamola con lo spazio concentrato in una retta.

s = s’ + vt

t = t’                  …. (2)

Nel nostro caso particolare, abbiamo un sistema con origine in P che si muove di moto rettilineo uniforme, con velocità v_PO, rispetto a un sistema che ha origine in O. All’istante t_O La coordinata spaziale di P rispetto al suo sistema di riferimento (s_PP) è zero (P è l’origine). La coordinata spaziale di P rispetto a O è invece s_PO.  Se scriviamo la trasformazione di Galileo con le nuove notazioni, abbiamo:

s_PO = s_PP + v_POt_O = 0 + v_POt_O = v_POt_O

t_O = t_P

Ovviamente è la stessa cosa che avevamo descritto prima.

Per capire ancora meglio come vanno le cose, consideriamo un evento P’, che non è altro che la posizione spazio-temporale di P a un certo tempo t_P’ = t_O’. Questo evento P’ (solidale col sistema di P) ha, adesso, una sua coordinata spaziale rispetto a P, s_PP’ che è diversa da zero. Tuttavia la velocità di P’ rispetto al sistema di O è sempre la stessa, dato che sta sulla linea di Universo di P (v_P’O = vP_O). La coordinata spaziale di P’ rispetto a O è s _P’O. In queste condizioni possiamo scrivere:

s_P’O = s_P’P + v_PO t_P’

t_O’ = t_P’

E’ di nuovo la trasformazione di Galileo, ovviamente, scritta nella sua forma classica. Queste banali rappresentazioni ci fanno però capire come il tempo abbia ormai assunto una vera e propria fisionomia di coordinata. Lo trattiamo tranquillamente sia nel presente come nel futuro e lo potremmo anche fare nel passato. Anche se rimane ancora qualcosa di assoluto (è sempre lo stesso in ogni sistema di riferimento) ha già cambiato forma e sostanza. Stiamo veramente lavorando in uno spazio-tempo per semplificato che sia. Le posizioni sono diventati eventi che rispettano la relatività galileiana. Pensiamoci bene sopra, dato che è un concetto che sarà fondamentale quando le cose si complicheranno.

Bene, adesso possiamo divertirci a disegnare, sempre in Fig. 8, qualcosa di più … complicato. Poniamo ad esempio, che ci sia un altro personaggio Q che, all’istante t = 0, sia insieme a noi (O e P). Anche lui non vuole stare fermo e si muove di moto rettilineo uniforme rispetto ad O. Anzi, va molto veloce, ossia v_QO > v_PO. La sua linea di Universo non può essere altro che quella rossa. Il nostro spazio-tempo funziona molto bene, dato che è facile verificare che se Q si muove lungo una linea retta rispetto a O, esso si muove anche secondo una linea retta rispetto a P. D’altra parte sappiamo che le velocità si sommano, ossia:

v_QO = v_QP + v_PO

Lascio a voi la semplice verifica di quanto ho appena detto, facendo le differenze tra le tre linee di Universo lungo le linee orizzontali rosse che rappresentano eventi che si verificano in tempi uguali.

Devono, ovviamente, valere sia la trasformazione galileiana che la composizione della velocità.

Cambiamo sistema di riferimento

Finora abbiamo considerato il sistema di O come quello di riferimento. Possiamo cambiare sistema di riferimento? Sicuramente, dato che sono inerziali, non deve modificarsi niente: ciò che era inerziale deve continuare a essere inerziale. Cambiamo persona e diventiamo P. Adesso  è P che sta fermo e descrive la retta verticale t = 0. Trasformiamo, perciò, lo spazio-tempo riferito a noi con lo spazio-tempo riferito a P.

Cosa dobbiamo fare? Semplicissimo: ruotiamo la linea azzurra fino a farla coincidere con quella nera. Le altre due devono ruotare di conseguenza, mantenendo le stesse distanze tra di loro. Otteniamo la Fig. 9. Il tempo, ovviamente, deve restare quello che è.

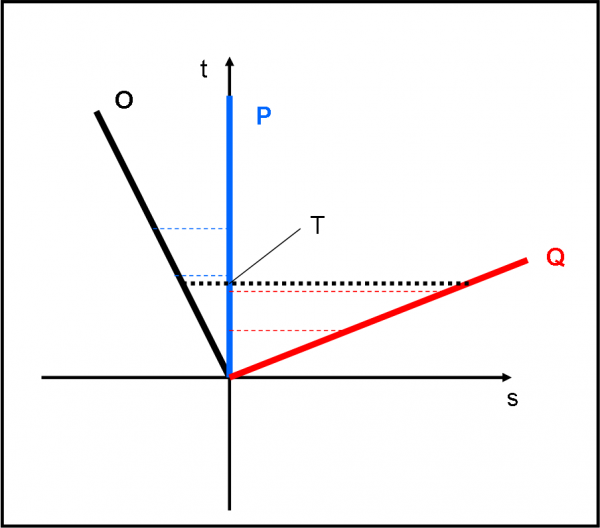
Non ne siete convinti? Il segmenti rossi tratteggiati di Fig. 8 sono esattamente gli stessi che abbiamo riportato in Fig. 9. La stessa cosa capita per i segmenti tratteggiati blu. Si vede bene che la linea rossa rimane una retta anche rispetto a P, preso come sistema di riferimento. Non dobbiamo certo stupirci dato che linee di universo rettilinee indicano sistemi tra loro inerziali. Un moto rettilineo uniforme resta tale passando da un sistema di riferimento a un altro. Proprio ciò che ci dice Galileo!

Non fatemi scrivere ulteriori formule che sarebbero sempre le stesse. Conviene capire il succo solo graficamente. E’ sicuramente più semplice, anche intuitivamente. E non chiedetemi perché ho ruotato la linea blu e non l’asse dello spazio. E’ una condizione ovvia, dato che adesso è P che rimane fermo e quindi deve muoversi solo lungo l’asse del tempo. In poche parole, la trasformazione ha mantenuto i moti relativi tra le tre linee di Universo, proprio come vuole Galileo. Ma, soprattutto, notate che gli eventi neri, blu e rossi, avvengono sempre allo stesso tempo, indipendentemente dal sistema di riferimento utilizzato. Ciò vuol dire, in “soldoni”, proprio che per Galileo il tempo è assoluto e non cambia a causa di trasformazioni.

In parole più generali: se disegno una retta parallela all’asse s (ossia una retta che identifica un tempo t uguale per tutti) come quella nera puntinata di Fig. 8, essa identifica gli stessi eventi anche dopo avere applicato la trasformazione di sistema di riferimento, in Fig. 9. Eventi che avvenivano nelle tre rette a un certo istante T, continuano ad avvenire sempre in quel momento. Pur cambiando sistema di riferimento, il tempo di un certo evento non cambia. Gli orologi dei tre sistemi in moto inerziale segnano sempre la stessa ora quando accadano gli stessi eventi.  Più tecnicamente: la trasformazione di Galileo conserva la simultaneità degli eventi. Che frase importante è questa! Fondamentale per la relatività. Teniamola in dovuto conto perché non ce la toglieremo più dai piedi…

Provate a cambiare ancora il sistema di riferimento e considerare fermo quello rosso. Disegnate da soli la trasformazione e poi controllate, con la Fig. 10, se tutto è andato bene…

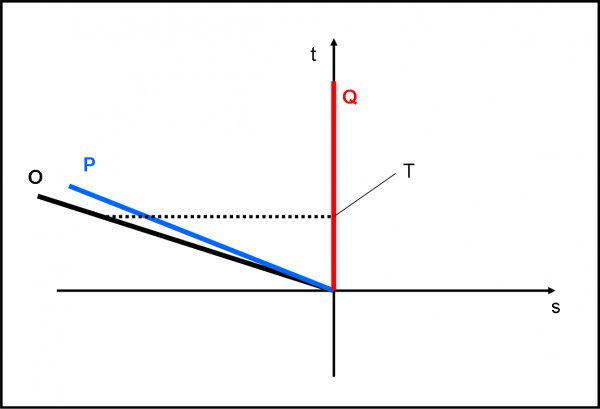
Lo ammetto, i diagrammi spazio-tempo di Galileo sono decisamente semplici. Tuttavia, conviene digerirli molto bene per valutare al meglio la rivoluzione di Einstein.

Lo spazio è già diventato “relativo”

Analizziamo ancora meglio la definizione di “relatività” galileiana. Sembra ormai di averla compresa perfettamente, quando si dice che le leggi della meccanica sono le stesse in tutti i sistemi di riferimento inerziale. Questa frase si lega perfettamente alla trasformazione di coordinate e alla composizione delle velocità. Perché allora chiamarla “relatività”?

La risposta è semplice: “essa impone un tempo assoluto, ma non uno spazio assoluto”. In altre parole, lo spazio è relativo all’osservatore. Due osservatori che si muovono, l’uno rispetto all’altro, di moto rettilineo uniforme non sono assolutamente in sintonia quando descrivono lo spazio percorso da un terzo oggetto, anch’esso in moto rettilineo uniforme rispetto a loro. Questa conclusione porta proprio a dire che lo spazio è relativo all’osservatore. Il tempo invece rimane lo stesso. Metà teoria della relatività ristretta è quindi giù impostata nei grafici che abbiamo visto finora. Vogliamo averne una conferma ulteriore? Lo so che sto girando attorno a banalità, ma è sempre meglio vedere il problema da tutti i punti di vista.

Immaginiamo, In Fig. 11a, di essere su un’astronave A nello spazio vuoto, ma così vuoto che lo spostamento della nostra astronave non possa essere assolutamente percepito da noi che stiamo all’interno. Non esiste vibrazione alcuna e non vi è niente che possa essere preso come punto di riferimento. Nel solito diagramma noi ci sistemiamo lungo la linea verticale (linea di universo nera). Non c’è nessun problema a considerarci fermi, anzi noi siamo sicuri di essere fermi.

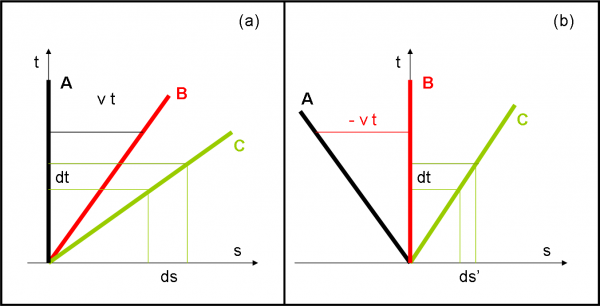
Finalmente, a un certo momento, ecco comparire un’altra astronave B che ci raggiunge da dietro e ci supera con grande facilità. Cosa possiamo concludere? Che essa sta viaggiando a grande velocità. (Attenzione: riducendo lo spazio a una sola dimensione è ovvio che quando l'astronave ci raggiunge coincide proprio con noi. In realtà essa può avere y e z diversi...).

Nel nostro sistema di riferimento possiamo disegnare la linea di universo dell’altra astronave (linea rossa). La sua velocità è costante e nell’unità di tempo descrive un certo spazio.

La stessa cosa, però, dice anche l’equipaggio dell’altra astronave (B). Il suo equipaggio è convinto di non muoversi e pensa che siamo noi (A) ad andare a marcia indietro, a grande velocità. Bene, lei può benissimo rappresentare se stessa nel diagramma (Fig. 11b) come linea verticale (rossa) e disegnare la nostra linea di universo come linea nera. Poco male, in fondo, le due velocità hanno solo cambiato di segno, ma hanno lo stesso modulo. Per l’altra astronave siamo noi a percorrere lo stesso spazio nella stessa unità di tempo. Cambia solo il verso del moto.

Immaginiamo adesso che mentre noi (A) e gli altri (B) stiamo facendo questi bei calcoletti (perfettamente in linea con i principi di Galileo), appaia un terza astronave C (probabilmente aliena, dato che la disegniamo verde come i… marziani).

A noi sembrava che l’astronave “amica” andasse veloce. Assolutamente no: questa sembra solo un puntino, ma in brevissimo tempo supera sia noi che l’altra. Nel nostro sistema di riferimento (Fig. 11a) facciamo in fratta a disegnare la sua linea di universo verde e possiamo dire con sicurezza che ha percorso un certo spazio ds nell’unità di tempo dt.  Cosa dicono, invece, i nostri amici dell’astronave B? Anche loro vedono andare veloce l’astronave aliena, ma non certo come la vediamo noi. Se essi tracciano la linea verde nel loro sistema di riferimento (Fig. 11b), dicono che C ha percorso un certo spazio ds’, sempre nella stessa unità di tempo dt, identica alla nostra. Ma ds’ è nettamente inferiore a ds e, quindi, cosa possiamo concludere? Semplice: lo spazio, percorso da un oggetto in movimento rettilineo uniforme, è RELATIVO al sistema di riferimento da cui si osserva. E’ o non è una teoria della relatività molto … ristretta?

Tempo e lunghezze  assolute

Quanto appena detto non deve, pero, confonderci. Anche se lo spazio è relativo al sistema di riferimento, le misure di lunghezza e di intervalli di tempo restano immutati qualsiasi sia il sistema di riferimento inerziale da cui si osservano. Questo fatto non deve essere dimenticato, dato che è proprio quello che ci mostrerà le maggiori differenze rispetto alla visione relativistica di Einstein. Scusate se batto ancora sullo stesso chiodo, ma è fondamentale non avere dubbi.

Sappiamo ormai molto bene, proprio per ciò che dice la trasformazione galileiana, che il tempo scorre nello stesso modo in qualsiasi sistema di riferimento inerziale. In altre parole, un orologio che si trova sopra una nave che viaggia velocemente rispetto a noi, che ci consideriamo fermi, rimane sempre sincronizzato con il nostro. Diciamo ancora meglio questo dato di fatto. Se noi guardiamo il nostro orologio e quello della nave li vediamo andare d'amore e d'accordo. Ne segue che gli intervalli di tempo rimangono uguali.  Stiamo bene attenti a ciò che questo vuol dire: chi  viaggia su una nave vede girare il suo orologio nello stesso modo di come noi, fermi, vediamo girare il nostro orologio. Tuttavia, chi viaggia  e chi sta fermo non possono  confrontare direttamente come scorre il tempo dell'altro. Non possono certo sdoppiarsi. l'unico modo per farlo è guardare, dal proprio sistema di riferimento, come gira l'orologio dell'altro.

Notate la differenza essenziale: una cosa è vedere girare il proprio orologio in diversi sistemi di riferimento e un'altra cosa è vedere girare, dal proprio sistema di riferimento, quello che si trova all'interno di un altro sistema di riferimento. Non confondiamo le due situazioni!

Nella relatività galileiana tutti questi tempi sono uguali. In particolare, come già detto, un intervallo di tempo è lo stesso in ogni sistema ed è lo stesso se visto da qualsiasi sistema inerziale. Ciò deriva dal fatto che t' = t. Per un intervallo di tempo tra due eventi (P e Q), si ha:

t_P –t_Q = t’_P –t’_Q

L'intervallo di tempo tra due eventi rimane lo stesso, qualsiasi sia il sistema di riferimento da cui si osserva.

Consideriamo, adesso, una lunghezza spaziale. Ad esempio, un righello che ha per estremi A e B. In questo caso A e B sono posizioni spaziali e non eventi, ovviamente.

Il righello sia situato nello spazio del nostro sistema di riferimento fermo. Come viene visto il righello da colui che viaggia a velocità v rispetto a noi? Beh... semplice lui vede tutto ciò che fa parte del nostro spazio muoversi a velocità uguale e contraria, ossia -v. Con la scelta che abbiamo fatto, possiamo tranquillamente sostituire al vettore il suo modulo.

La trasformazione galileiana dice che:

s’_B = s_B – vt_B

s’_A = s_A – vt_A

da cui:

s’_B- s’_A = s_B – s_A - v(t_B – t_A)

Tuttavia, le posizioni di A e B (che sono punti) vengono misurati nello stesso istante di tempo, ossia:

t_B = t_A

Sostituendo, si ha:

s’_B - s’_A = s_B – s_A

la relazione ci dice che anche la distanza tra due punti, ossia la lunghezza di un righello, rimane la stessa qualsiasi sia il sistema di riferimento da cui si guarda e si misura. Possiamo perciò concludere che: secondo la trasformazione galileiana le misure di intervalli temporali e spaziali sono ASSOLUTE, cioè indipendenti dal sistema riferimento inerziale da cui si effettuano le misure.

Probabilmente ho ripetuto le stesse cose fino alla nausea. Però, vi prego di leggere e rileggere molto bene ogni cosa che ho scritto. Se qualcosa non vi non torna perfettamente, bloccatemi subito (anche privatamente). Se fosse necessario, potrei anche aggiungere parti e figure o espandere di più e meglio certi concetti, in modo da soddisfare tutti gli interessati. Magari fatevi anche qualche disegnino da soli, complicando leggermente la situazione e poi valutate se sono sorti dubbi o difficoltà.

Sono costretto a ribadire ancora una volta che se esistono problemi con la trasformazione galileiana, quando il tempo si metterà a variare con lo spazio e lo spazio si muoverà come una fisarmonica, non ne usciremo più vivi… Mi raccomando!