Categorie: Spazio-Tempo
Tags: curvatura relatività generale spazio spaziotempo velocità verso la RG
Scritto da: Vincenzo Zappalà
Commenti:38
Spazio e spaziotempo: a ognuno la sua curvatura ***
Questo articolo ci mostra, qualitativamente, come la relatività generale implichi una curvatura dello spaziotempo e non solo dello spazio. Purtroppo, noi intuiamo abbastanza bene solo la seconda. Limitandosi ad essa, la relatività sarebbe un’assurdità. Non ci sono formule, ma il concetto non è banalissimo, benché fondamentale per immergersi veramente nella problematica dei buchi neri e non solo. Non fatevi ingannare dall’apparente banalità: se capite l’essenza del concetto di base, tutto sarà più facile.
Andiamo per gradi, scoprendo alcune ovvietà che forse non sono tali per tutti. Immaginiamo di usare tre metodi per lanciare un sasso: farlo cadere per terra, usare la forza muscolare e usare una pistola lancia sassi (se non esiste la fabbrichiamo noi). Come al solito, escludiamo l’atmosfera terrestre e tutto ciò che può dare fastidio a una trattazione teorica. Sappiamo già che la massa m del sasso NON conta (a parte la forza che bisogna imprimergli per lanciarlo lontano da noi) e che, qualsiasi essa sia, il tempo di caduta resta sempre uguale (se non ci credete chiedete a Galileo Galilei, ma l’abbiamo dimostrato varie volte anche noi…). Per semplificare la faccenda consideriamo che la direzione del lancio (se lancio esiste) sia perfettamente parallela alla superficie terrestre. Insomma, spariamo o lanciamo in direzione orizzontale. La Fig. 1 ci mostra la situazione e il risultato.
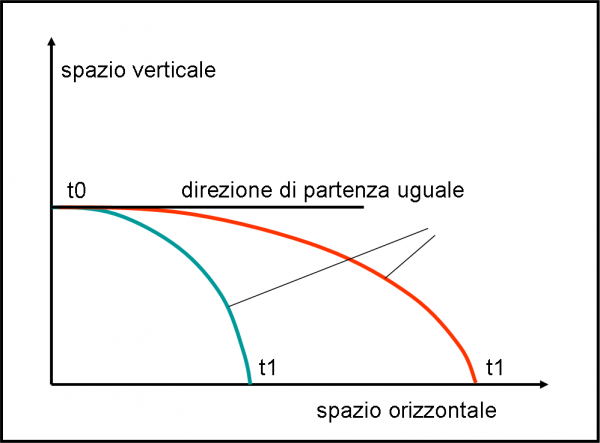
Possiamo, innanzitutto, concludere che il sasso tocca terra nello stesso identico istante. Infatti, la velocità impartita al sasso sia con i muscoli che con la pistola è sempre diretta in modo perpendicolare alla direzione della forza di gravità. La velocità, quindi, non viene “influenzata” dalla gravità e continua a restare costante. La durata del volo dipende, perciò, solo e soltanto dall’accelerazione di gravità che “abbassa” sempre di più il sasso. Ne segue che il tempo di caduta è indipendente dalla velocità data al sasso. Non ci dobbiamo stupire, quindi, se i tre sassi cadono a terra nello stesso momento. Quello che cambia sicuramente è lo spazio percorso.
Per i nostri scopi, questo non è molto importante, ma è sempre bene tenerlo a mente. In qualche modo ci serve per stabilire una costanza nel tempo. Lasciamo da parte il sasso che cade a terra senza avergli dato velocità (potrebbe confondere ancora di più le idee) e soffermiamoci sugli altri due.
Essi partono dallo stesso punto e con la stessa direzione, ma raggiungono distanze diverse. La cosa non dovrebbe certo spaventarci rimanendo nella meccanica newtoniana. Ciò che vediamo (a parte il tempo uguale di caduta che potrebbe sorprendere qualcuno) fa parte della nostra vita quotidiana e si spiega perfettamente con l’esistenza di una forza attrattiva (legge di gravitazione universale).
Tuttavia, Einstein ha detto che, in realtà, non esiste nessuna forza e che la traiettoria di caduta dipende solo e soltanto dalla curvatura dello spazio-tempo, creata dalla massa della Terra. Fingiamo di non aver capito bene le parole di Einstein e consideriamo solo una curvatura dello spazio (errore che si commette spesso anche per colpa delle figure che vengono usate per spiegare la deformazione einsteniana).
In poche parole, se accettiamo che la caduta del sasso dipende da una curvatura dello spazio, dovremmo sorprenderci del fatto che i due sassi non percorrono la stessa traiettoria. La nuova logica sembra implicare proprio questa soluzione. Infatti, l’unica differenza che appare ai nostri occhi è la differente velocità che viene impartita ai sassi, mentre la direzione di lancio è la stessa. Se tutto dipende da una curvatura dello spazio, perché mai le traiettorie finali sono diverse? In poche parole, la Terra dovrebbe essere circondata da uno spazio curvo che agisce su ogni cosa nello stesso modo. E’ la curvatura che decide la traiettoria da seguire. La velocità non dovrebbe avere nessuna influenza. Lasciata andare a una certa altezza e con una certa direzione il sasso cade per terra perché segue una traiettoria curva dovuta a uno spazio curvo. Punto e a capo! Al limite, un sasso percorre la traiettoria a velocità maggiore dell’altro.
Ragioniamo bene attorno al problema che ci si para davanti. Abbiamo due sassi che partono dallo stesso punto e che si muovono nella stessa direzione. Non subiscono forze ma solo una curvatura dello spazio. E’ proprio quella che li fa cadere per terra. Non possiamo che concludere che le loro traiettorie devono essere uguali.
Rileggiamo bene le assunzioni di Einstein: “La curva che il sasso sembra compiere nello spazio è dovuta solo alla sua curvatura. In realtà i due sassi si muovono entrambi secondo linee rette nel loro spazio a due dimensioni. Una questione di pura geometria curva. Facciamo un esempio molto illuminante. Pensiamo a una curvatura costante come quella di una sfera, proprio come la nostra Terra. I due sassi possono esser pensati come due persone che si muovono nel loro spazio curvo a due dimensioni. Partono dallo stesso punto e vanno nella stessa direzione, ma con velocità diverse.
Se vanno nella stessa direzione non possono che seguire la stessa traiettoria. Il primo cammina lentamente, il secondo corre, ma ciò che conta è che entrambi devono arrivare nello stesso punto dello spazio. Poche storie, se prendono la stessa strada devono arrivare nella stessa città! E invece la realtà ci dice che ciò non succede: i due sassi compiono traiettorie spaziali nettamente diverse.
Insomma, Einstein ha detto cose non vere. La teoria sarà anche bella, ma le osservazioni indicano nettamente il contrario: pur avendo la stessa direzione di partenza le due traiettorie differiscono in quanto a spazio percorso.
Ma ne siamo proprio sicuri? Direi che abbiamo commesso una bella svista… Abbiamo considerato che fosse la stessa cosa dire: spazio curvo e spaziotempo curvo. E invece il succo della questione sta tutto lì. Malgrado abbiamo usato spesso lo spaziotempo, il vero legame tra spazio e tempo continua a sfuggirci. Proviamo ancora una volta…
Disegniamo, in Fig. 2, le traiettorie dei nostri due sassi in un sistema di riferimento lontano dalla nostra visione normale. Nell’asse delle x continuiamo a mettere la distanza spaziale raggiunta dai due sassi nel momento che toccano terra. Nell’asse y, invece, mettiamo il tempo passato dal momento del lancio. In questa figura le due traiettorie spaziotemporali divergono istantaneamente. Più passa il tempo e più lo spazio percorso è diverso. D’altra parte, dovevamo aspettarcelo: in questo diagramma la velocità la fa da padrona. Essa è proprio ciò che collega spazio e tempo!
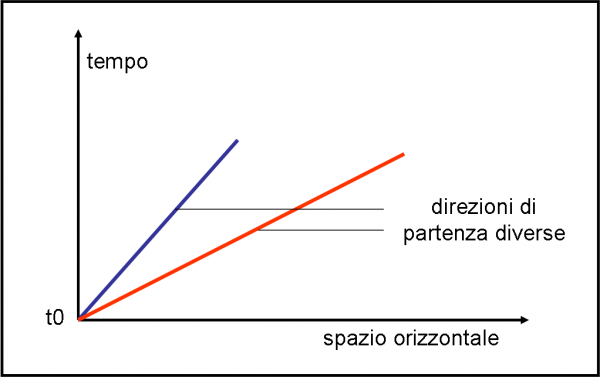
Nello spaziotempo curvo le due traiettorie non sono più le stesse per ragioni ovvie: i due sassi partono con direzioni diverse! Uno prende una strada e l’altro ne prende un’altra. Non possiamo certo aspettarci che arrivino allo stesso punto finale. Nello spaziotempo, la traiettoria che deve essere considerata è quella della nuova figura.
Cosa deve succedere, allora, affinché due sassi seguano la stessa traiettoria nello spazio tempo? Non basta che seguano la stessa direzione (come nel caso spaziale), ma devono anche avere la stessa velocità. proviamo, infatti, a lanciare i nostri due sassi con la stessa direzione spaziale e con la stessa velocità. Adesso sì che le cose funzionano. Le due linee di Fig. 2 coinciderebbero! E poco importa se uno è più pesante dell’altro, l’importante è che siano sulla stessa strada spaziotemporale.
Questo è proprio quello che dice la teoria di Einstein: “ La traiettoria di un oggetto nello spaziotempo non dipende dalla massa dell’oggetto ma solo e soltanto dalla direzione iniziale”. Ma la direzione è la direzione spaziotemporale e non solo spaziale!
Per concludere cerchiamo di riassumere quanto abbiamo imparato: il campo da gioco che dobbiamo considerare nello spiegare gli eventi del cosmo non può mai essere solo lo Spazio. Tutto esiste solo in un teatro spaziotemporale. Se consideriamo la curvatura solo come una rappresentazione spaziale, abbiamo una visione approssimativa della realtà.
Come promesso, nessuna formula, ma solo un concetto che fatica a saltare all’occhio. L’importante è riflettere sempre bene se si sta lavorando nello spazio o proprio nello spaziotempo. Anche il famoso “imbuto” prende consistenza se riusciamo a visualizzarlo (o meglio estrapolarlo) in uno spaziotempo. Ecco perché sarà sempre più utile una rappresentazione spaziotemporale che tenga conto della relatività ristretta…
Questo articolo fa parte della serie "Verso la RG", in quanto propedeutico alla comprensione della Relatività Generale, QUI trovate tutti quelli che sono stati scritti fino ad ora.
QUI trovate l'approfondimento dedicato alla Relatività Generale





38 commenti
Caro Enzo, mi sembra che tu inizi a fare come certi redattori capo dei quotidani i quali decidono dei titoloni a cui non corrisponde il contenuto dell'articolo!
OHE', STO SCHERZANDO EH?
La verità è che il titolo del tuo articolo è molto stimolante. Non voglio anticipare quello che presumo spiegherai nella serie dedicata allo S-T di Minkowski, ma .....
SPAZIO:
Lo spazio (tridimensionale) del cosmo (universo osservabile) sembra rispondere alla geometria euclidea, presentandosi pressochè PIATTO (inflazione ecc. ecc.). Ovviamente non teniamo conto della curvatura locale prodotta dalla presenza di oggetti massivi.
In questo caso l'espressione che permette di calcolare la DISTANZA dS tra due punti assume la forma:
dD^2 = dx^2 + dy^2 + dz^2 (teorema di Pitagora).
Secondo la RR, per un osservatore O in moto a velocità relativistica, lo spazio nella direzione del moto si accorcia. Tale effetto può essere rilevato da un secondo osservatore O' "fermo (*)", visto che anche i regoli di O si accorcerebbero come gli oggetti che O decidesse di misurare. Ne deriva che dD dipende dall'osservatore.
(*) Quale dei due è fermo e quale in moto? Diciamo che inizialmente erano entrambi sulla Terra, dopodichè uno si è imbarcato su un razzo interplanetario acquisendo un'accelerazione iniziale molto intensa per poi procedere per inerzia.
SPAZIO-TEMPO:
Lo spazio-tempo (quadridimensionale) risponde invece, secondo la RR, ad una geometria diversa. Infatti l'espressione che permette di calcolare la SEPARAZIONE dS tra due punti-evento (per la RR dS è sempre la stessa, quale che sia l'osservatore) assume la forma:
dS^2 = (ct)^2 - dx^2 - dy^2 - dz^2
Si nota subito che la diversità di segno attribuito a ct (positivo) ed agli altri termini al secondo membro (negativo) allontana detta espressione dal teorema di Pitagora. Dunque? Beh, sembrerebbe che lo S-T quadridimensionale presenti una geometria NON PIATTA anche in assenza di masse.
Se non ho scritto un cumulo di sciocchezze mi sembra che la questione sia piuttosto interessante, anche perchè si potrebbe essere indotti a pensare che sia la massa a produrre la curvatura dello S-T, mentre quest'ultimo lo è già di suo. La massa, laddove presente, imprime quindi un'ulteriore curvatura.
Corretto Enzo, o leggo troppi romanzi di fantascienza?
caro Alvy,
lo spaziotempo diventa curvo solo se entri nella relatività generale. La RR non si occupa di accelerazioni e quindi nemmeno di gravità... lo spaziotempo di Minkowski è piatto per definizione.
L'insieme di tutte le masse può portare a uno spazio curvo generale, da non confondere con la curvatura locale...
L'articolo definisce solo quali sono le prerogative per uno spaziotempo curvo... in RG (se fosse RR non ci sarebbe curvatura a causa di massa)
Ma allora Enzo, qual'è il SENSO dell'espressione che fornisce la separazione nella RR?
dS^2 = (ct)^2 – dx^2 – dy^2 – dz^2
Io mi rifaccio al teorema di Pitagora (disatteso dalla formula di cui sopra) che definisce uno spazio piatto, ma forse sbaglio ...
In altri termini, mi aspetterei di vedere tutti segni positivi al secondo membro dell'espressione. Come si concilia una tale espressione con uno S-T piatto?
è uno spazio piatto a 4 dimensioni...
Perdona l'insistenza Enzo ma ... quindi la distanza tra due punti in uno spazio piatto a 4 dimensioni si calcola con la formula di cui sopra ..... mmmh bene, bene.
Visto che il teorema di Pitagora va bene sia in 2 che in 3 dimensioni (spazio piatto) , pensavo che mantenesse la stessa forma anche in 4 dimensioni, e invece .... però che strano ...
Bene, questa non la sapevo. Come vedi, caro Enzo, ne ho di cose da imparare .... sta tranquilo che nel tuo blog non mi annoio di sicuro!
caro Alvy,
vedi che il mio "battere" sulla curvatura ha una sua ragione... Esiste uno spazio a due dimensioni piatto e uno spazio a due dimensioni curvo (piano e superficie sferica, ad esempio). Esiste uno spazio a 3 dimensioni piatto (euclideo) e curvo (non euclideo). Analogamente esiste uno spazio a 4 dimensioni piatto e curvo. Ciò che fa Minkowski è legare le 4 coordinate in uno spazio tempo, ma non curva niente. Solo la RG introduce la curvatura...
aggiungo, se ti può servire... la relazione che riporti tu esiste quando hai applicato la trasformazione di Lorentz e serve a descrivere un'invariante in quello spaziotempo. Chiamala se vuoi "separazione" spaziotemporale. Il fatto che può diventare minore di zero, dipende dalla separazione del diagramma di Minkowski tra eventi tipo spazio e eventi tipo tempo, separati dal cono di luce... ma è inutile proseguire per frasi smozzicate. Bisogna che inizi veramente con le trasformazioni di Lorentz e con la sua rappresentazione grafica. In questo modo si fa solo confusione, credimi...
OK, seguiamo pure la strada maestra, senza fretta.
Mi rimetto in riga seguendo la ... dello S-T.
dello S-T.
Caro Enzo, aspettavo con ansia che riparlassi di spazio-tempo.
Hai perfettamente ragione! E' praticamente impossibile da visualizzare, di recente ho trovato una frase che riporto perchè ha chiarito un mio dubbio (Se non c'è l'attrazione di Newton come facciamo a stabilire il verso di percorrenza?), la frase: Il verso di percorrenza è dal tempo più veloce al tempo più lento.
Aspetto il tuo commento.
Grazie in anticipo.
caro Gaetano,
direi che ha un senso... l'accelerazione va verso la massa e quindi la velocità aumenta sempre più e ne segue che il tempo rallenta. Comunque, io direi che è più una conseguenza che una causa... Anche nella relatività generale il verso è individuato dalla curvatura che aumenta andando verso la massa.
Ah Gaetano... se leggi la risposta al buco nella Terra, vedrai che alla fine si parla di nuovo di curvatura dello spazio-tempo...
Enzo, però il tempo è legato anche alla massa, non solo alla velocità! Infatti nel B.H. teoricamente (nel senso che difficilmente si potrà provare ) il tempo si annulla.
) il tempo si annulla.
Visto che Enzo è impegnato a ballare ed a suonare le lingue di Menelik cerco di risponderti in attesa che la nostra guida si riappropri del suo ruolo e mi bacchetti!
Dunque caro Gaetano,
le grandezze in gioco sono tra loro legate: se aumenta la massa attraente aumenta l’attrazione gravitazionale che produce un aumento della velocità (accelerazione); l’aumento della velocità a sua volta produce il rallentamento del tempo.
La causa scatenante è la massa, che produce una distorsione (curvatura) nella trama dello spazio-tempo: l’aumento della velocità e la dilatazione del tempo vanno di conseguenza.
In definitiva si può dire che lo scorrere del tempo (variabile) discende dal valore della velocità (variabile) che, a sua volta, dipende dalla massa (variabile).
Lo stesso effetto si ottiene se anzichè variare la massa si varia la distanza da essa: anche in tale caso infatti si ha a che fare con un aumento della curvatura dello S-T con ciò che ne segue.
Il buco nero è semplicemente una massa attraente, almeno finchè si resta fuori dall'orizzonte degli eventi. Che poi il tempo si annulli, beh, a furia di rallentare dovrà pur fermarsi prima o poi visto che il BN è un "pozzo senza fondo"!
Se manca la massa attraente, la velocità è costante (caso della relatività ristretta in cui si considerano solo moti inerziali in assenza di masse attrattive), ma può essere più o meno elevata. In questo caso si può dire che lo scorrere del tempo (costante, ma diverso per ciascun osservatore dotato di una sua velocità propria) discende dal valore della velocità (costante).
Non dimentichiamo che quanto detto a proposito del tempo vale anche per lo spazio, nel senso che anch'esso subisce un'alterazione: insomma si deve parlare di spazio-tempo anzichè di spazio o di tempo perchè le due grandezze sono intimamente connesse.
Spero di essere stato chiaro. Comunque per la conferma della correttezza di quanto ho scritto attendiamo il ritorno del grande capo!
direi che Alvy è stato abbastanza preciso.
in poche parole: è la massa (o meglio la densità, ossia quanta massa sta in un certo volume) che causa la curvatura dello spazio-tempo ed è quindi ovvio che spazio e tempo dipendano dalla curvatura e quindi dalla densità. L'orizzonte è proprio il punto in cui la curvatura fa sì che il tempo, visto dal di fuori, abbia una asse perpendicolare a quello dell'osservatore esterno o, meglio, la linea della velocità della luce rispetto all'asse del tempo curvato è parallela all'asse del tempo dell'osservatore. Ciò vuol dire che la luce inviata da chi sta per cadere dentro l'orizzonte arriverà all'osservatore solo in un tempo infinito...
Ovviamente, il tutto dipende dalla curvatura dello spaziotempo e quindi dalla massa che lo deforma (meglio ancora la densità).
Alvermag, ringrazio ma forse non ho chiarito bene il mio dubbio. Tutte queste cose penso di averle già digerite. Einstein (e Enzo conferma nel suo articolo) ha eliminato l'attrazione di Newton, c'è solo la massa/energia che curva lo spazio-tempo, gli oggetti si muovono lungo queste geodetiche. Le geodetiche non hanno (?) un percorso preferito quindi cosa decide da che parte andare? La frase che dice che la direzione è dal tempo più veloce al tempo più lento l'ho trovata ne "Il piccolo libro delle stringhe" di S. Grubser (tra l'atro molto interessante!). Non è una spiegazione ma è un modo per spostare il problema, secondo me, su una questione più comprensibile. Buon 2015 a tutti.
Come preferisci Gaetano...
a me personalmente riesce più intuitivo pensare a linee che vengono deformate dalla curvatura piuttosto che pensare al tempo come una variabile che decide i percorsi... E chi è che lo fa variare? L'importante è, comunque, che si capisca il concetto!
Penso siamo tutti d'accordo sul fatto che l'attrazione di Newton sia più intuitiva. Le masse si attragono e la forza è proporzilale alle masse in gioco. Poi Einstein elimina l'attrazione e dice che le masse distorcono lo spazio-tempo e tutti pensiamo al lenzuolo con una grande palla al centro e le palle più piccole che si comportano come la pallina della roulette. Il mio dubbio è come si decide l'alto e il basso se non c'è attrazione. Enzo non ho preferenze, proprio non riesco a capire.
caro Gaetano,
non esiste un alto e un basso: esiste solo una curvatura intrinseca dello spazio. Nel caso di uno spazio a due dimensioni si disegna una specie di imbuto in una terza dimensione "fasulla" (estrinseca) solo per rendere l'idea. Nell'articolo di poco precedente ("attenzione all'imbuto") cerco proprio di spiegare come si costruisce questa figura molto usata, ma da prendere con le dovute cautele. Parlo anche del fatto che non esiste nessun lenzuolo che si comprime in una certa direzione, ma un lenzuolo che è curvo di per sé. Bisogna pensare a una superficie bidimensionale non euclidea, dove le rette non sono parallele ma convergono in un punto (da cui la curvatura intrinseca). Tieni anche conto che si parla di curvatura dello spaziotempo e non solo dello spazio... Il lenzuolo tanto usato è solo spazio e non spaziotempo...
Lo so, il concetto non è facile e proprio per questo cerco di descriverlo in tutti i modi possibile. Anche nella risposta al quiz sul buco della Terra, alla fine, riprendo il concetto di curvatura dello spaziotempo unidimensionale...
Il blog è interesante, ma mi dispiace che poi si finisca come il solito "all'italiana" ("liguaggio per iniziati"): cosa significano RG, RR?
Fino a S-T ci arrivo (Sopazio-Tempo) ma per il resto......
Non scoraggiate i novizi!
Quando lavoravo, mi occupavo di Ricerca di farmaci (nei miei articoli su riviste scientifiche anche straniere era PROIBITO non specificare, ogni volta, il significato delle sigle!), ora sono in pensione (attiva!).
Cordialità
Bruno, Monza
Bruno, un piccolo sforzo in più e ci arrivavi... RG relatività generale, RR relatività ristretta, parlando di spazio-tempo veniva automatico pensare ad Einstein.
Cordialmente
caro Bruno,
no... rifiuto che sia considerato il solito blog all'italiana, come dici tu... Il problema è che va seguito e non letto una tantum. Noi cerchiamo di impostare e descrivere ciò di cui si parla e non buttare giù informazioni saltuarie. Le pochissime sigle sono state stabilite in articoli precedenti. RR e RG è un po' come dire USA al posto di Stati Uniti d'America, così come MQ sta meccanica quantistica. Di sicuro non ne troverai altre...e soprattutto non definite esattamente. Il nostro è un processo divulgativo continuo e non un insieme di idee e notizie inserite senza alcun legame tra loro...
Ciao Enzo,
volevo essere sicuro di aver compreso bene la differenza tra spazio e spazio-tempo, e siccome stavo facendo un ragionamento un po' diverso dal vostro, provo a scrivere qualcosa in merito:
Lo spazio (che può avere ipoteticamente X dimensioni) può essere piatto o curvo (curvatura positiva o negativa). Dato che la materia è distribuita in maniera omogenea nel nostro Universo osservabile, possiamo idealmente "affettarlo" ad un determinato istante di tempo (nulla a che vedere con lo scenario spazio-temporale di Newton, ovviamente) e determinare il valore di Omega, ovvero il rapporto tra densità media e densità critica. Attualmente sembra che detto valore sia molto prossimo ad 1, dunque abbiamo a che fare con un Universo piatto, in cui è valida la geometria euclidea.
Lo spazio-tempo io tendo ad identificarlo come tutto l'Universo, ossia l'insieme di tutti gli eventi spazio-temporali. Ogni evento ha quattro dimensioni, tre spaziali ed una temporale. Anche lo spazio-tempo può essere piatto o curvo, ad esempio in quello piatto due particelle ferme col passare del tempo rimarranno ferme l'una rispetto all'altra, mentre nello spazio-tempo curvo positivamente come il nostro, in perpetua espansione, esse si allontaneranno le une dalle altre.
Quindi nel nostro caso abbiamo a che fare con uno spazio piatto e con uno spazio-tempo curvo.
caro SMA,
il tuo modo di ragionare potrebbe anche avere un senso... Tuttavia, continua a vedere il tempo come qualcosa di "aggiuntivo", indipendente dallo spazio. Le trasformazioni di Lorentz, però, ci dicono che il tempo e la direzione del moto (la x) sono strettamente collegate e che se cambia una deve cambiare anche l'altra. Diventa quindi fuorviante staccare lo spazio dal tempo. Le coordinate sono sempre quattro e la curvatura va intesa sempre su quattro dimensioni. Se non ci fossero masse non ci sarebbe accelerazione e varrebbe la RR che impone uno spaziotempo piatto. Solo l'accelerazione può curvare lo spaziotempo ed entriamo nella RG. L'importante è sempre avere bene in testa questo concetto di base. Attenzione, quindi a dire che t è costante. Se è t per un sistema di riferimento sarà t' per un altro.
L'espansione dello spaziotempo, inoltre, non implica automaticamente una curvatura. Anche per omega 1 vi è espansione... La distanza aumenta comunque.
Sempre che abbia compreso bene ciò che vuoi dire...
Forse mi sono espresso male ma non intendevo scollegare il tempo dallo spazio, la relatività ci dice che sono intimamente connessi, due diverse espressioni di un'unica entità, lo spazio-tempo.
Quello che intendevo era definire il tempo in modo tale che la densità di materia sia approssimativamente costante nello spazio (su larga scala).
In questo momento abbiamo un valore di Omega molto vicino a 1, quindi l'Universo è spazialmente piatto. La presenza di una costante cosmologica positiva invece, fa si che lo spazio-tempo sia curvo, in espansione perpetua.
Se per ipotesi Omega > 1, l'Universo sarebbe curvo positivamente e si chiuderebbe su se stesso come una sfera.
E' corretto?
beh... sì, in questo senso è corretto. Quando si definisce la densità critica, comunque, si parla solo di espansione e confrontando decelerazione con quantità di materia si ricava se è aperto o chiuso. Diciamo che la curvatura lega lo spaziotempo con la geometria in grado di descriverlo. Sono due discorsi relativamente separati...
La mia curiosità è questa: come fa la massa (o melgio: la densità) a creare la curvatura dello spazio-tempo? cioè cosa contiene la massa che genera il fenomemo? Inoltre vorrei sapere se la rotazione dei corpi è la conseguenza della deformaizne dello spazio tempo.
Spero proprio che qualcuno mi risponda. Grazie.
Petro Chichiarelli
Se vado veloce o più veloce nello spazio,visto che andiamo sempre a trecentomila /secondo,diminuisce la velocità del tempo.Un oggetto che ha piu velocità massa inerziale di un altro percorre ovviamente più spazio nell'unità di tempo,il sentiero però è lo stesso,dritto visto dall'oggetto,curvato se da un osservatore esterno,se la spinta è superiore alla forza di attrazione scappa via,la massa a riposo dell'oggetto non influisce sulla velocità di caduta.Ma la massa è importante per il percorso inverso,ovvero ci vuole più inerzia per sfuggire alla gravità.Un uomo alto normalmente ha pensieri più leggeri di uno basso,una donna alta a parità di taglia del reggiseno è più sicura del suo appeal.Se lo spazio tempo è curvo >1, gli uomini diventeranno serpenti alcuni con la gobba altri con la pancia.I serpenti più lunghi avranno problemi di comunicazione istantanea con la coda,potremo pestargliela e avere tutto il tempo per scappare.
Mi immagino la gravità e lo spazio come un immenso oceano liquido dove noi e gli altri oggetti siamo pesci.Questo liquido ha densità differenti,per cui noi scivoliamo senza accorgerci verso una composizione liquida più leggera,una corrente che ha i suoi movimenti a seconda del momento degli oggetti più massivi.Quando cadiamo sulla superficie di un oggetto massiccio,rimaniamo attaccati perché la corrente attraversandolo ci spinge sulla sua superficie.Se andiamo veloci,sempre più veloci il liquido dapprima impercettibile diventa poi un muro,come l'acqua,e come un natante abbiamo bisogno di molta energia per andare veloci.Se troviamo un oggetto supermassiccio la corrente che cade attraverso di lui ci attira come in un lavandino.Poco scientifico lo so.
Non so se quello che dici contiene la risposta alle mie domande, ma se così è ... non l'ho capita. Ripeto: cos'ha la massa (meglio: la densità) che genera la deformazione dello spazio tempo?
sarei felice se qualcuno me lo spiegasse.
caro Pietro,
al nostro Gianni piace spesso essere più poetico che scientifico... Cercherò di risponderti in modo più rigoroso...
La risposta non è certo cosa immediata e presuppone la conoscenza della relatività ristretta e generale. Tuttavia, semplificando, possiamo pensare che la massa sia energia, come dice Einstein e lo dimostra. Attorno a una massa si crea un campo capace di deformare lo spaziotempo, costringendo gli oggetti a seguire linee di Universo (traiettorie spaziotemporali, vedi Minkowski) che curvano, in modo analogo a un oggetto che si trovi su una superficie sferica. Ovviamente, più la massa è concentrata in un piccolo volume, più vicino puoi andare e la curvatura aumenta. La deformazione dello spaziotempo comanda il movimento dei corpi che sono costretti a seguire le linee di minore distanza quadrimensionale.
La massa è una caratteristica del corpo ed è tale da poter piegare il tessuto spaziotemporale. In realtà le masse sono due: inerziale e gravitazionale. La prima si oppone al moto, la seconda crea il campo deformante. Il grande mistero (o quasi) è che le due masse sono uguali e questo permette la trattazione di tutta la relatività generale (principio di equivalenza e cose collegate).
Nel nostro blog NON abbiamo ancora trattato la RG, dato che vogliamo creare le basi per capire. Troverai, perciò, tutta la RR e Minkowski... (approfondimenti). Si arriva alle grandi risposte costruendo piano piano il proprio bagaglio culturale.
Cosa intendi per rotazione dei corpi? Se è la rivoluzione attorno a un altro corpo (moto dei due corpi), la risposta è SI. La legge di Newton diventa la deformazione spaziotemporale. Se invece intendi rotazione attorno al proprio asse, la risposta è NO. In questo caso è solo un problema di momento angolare acquisito all'atto della formazione e/o da impatti successivi.
Grazie mille,
rifletterò a fondo su quello che hai scritto e cercherò di capire. La rotazione dell'astro che intendevo è quella attorno al proprio asse. Perdonami ma so già che ti chiederò altre spiegazioni: è tutto TROPPO interessante. Buona giornata.
grazie a te e a risentirci presto!
Caro professore, come preannunciato, dopo aver riflettutto e, soprattutto, letto sull'argomento, ho bisogno di chiedere ancora.
Ho sentito parlare solo di 'curvatura' dello spazio, causata (come mi hai spiegato) dalla massa-energia (o densità). Si tratta di un concetto abbastanza astratto perchè non mi sembra si riesca ad bene individuare la forma della curva (o delle curve), finendo per ipotizzarne tante e diverse tra loro (o mi sbaglio?).
Allora chiedo: invece di curvatura si potrebbe parlare di 'compressione' dello spazio? E' sbagliato immaginare che la massa attiri verso di sè lo spazio provocandone la compressione? Si tratterebbe di un fenomeno che potrebbe spiegare gli altri fenomeni collegati se si immagina che la compressione avrebbe (direi quasi: ovviamente) una intensità crescente in maniera costante man mano che ci si avvicina alla suerficie solida della massa. Da ciò si capirebbe il perchè la velocità di caduta di un corpo cresce in maniera costate. Questo potrebbe anche spiegare perchè il tempo è una variante dello spazio, ipotizzando che uno spazio più compresso rallenta lo scorrere del tempo, ovvero quel processo naturale che proprio di qualsiasi corpo o organismo, spiegaado anche perché nello spazio orbitale della terra il tempo scorre più velocemente rispetto alla superficie terrestre. Attraverso un successivo passaggio si potrebbe spiegare, inoltre, anche perchè l'aumento della volocità provoca il rallentamento del tempo.
Insomma, mi sembra un spegazione più logica e razionale rispetto a quella dell'esistenza di curve dello spazio che difficilmente riesco a conciliare concettualmente con l'armonioso moto dei corpi celesti.
Temo di aver detto un sacco di stupidagini, ma ti prego .... rispondimi lo stesso.
caro Pietro,
certe cose vanno digerite bene e con molta calma, senza cercare di trovare soluzioni alternative...
La curvatura che viene dedotta dalla RG è una curvatura spazio-temporale e non solo spaziale. La sua vera essenza dice che la minore distanza tra due punti (o se vuoi il tempo minore per andare da A a B) non segue una linea retta ma una linea curva, ossia lo spazio non è euclideo. Quale sia il legame tra spazio e tempo, ossia come si deformino a vicenda lo spiega perfettamente la RR. Siamo sempre alla solita vecchia storia... Bisogna fare propri i concetti di RR e DR per poi affrontare la RG e cercare di capirle perfettamente e non cercare, vista la difficoltà, di trovare soluzioni alternative.
Pensi proprio che Einstein & co. abbiamo trascurato soluzioni più semplici che anche chi conosce poco la fisica può prospettare? Ci vuole enorme umiltà e volontà di studiare fin dall'inizio i grandi temi della relatività e non solo... La fisica non si inventa dall'oggi al domani.
Grazie prof., faccio ammenda e continuo a studiare.
caro Pietro,
non bisogna avere fretta e cercare di fare propri i concetti di base, quelli che sembrano più facili, ma che poi creano i problemi... Cerca di comprendere bene la relatività della simultaneità e vedrai che lo spazio-tempo diventa un concetto quasi normale. Entrati in quel mondo, è molto più facile capire i legami che esistono tra queste grandezze e essere pronti alla curvatura e alla RG...
Tu hai la giusta predisposizione... non ti arrendere!!!!
Non riesco a capire.... I due sassi lanciati a due velocità diverse arrivano in punti diversi se considero la stessa durata del temèpo impiegato per atterrare e questo dipende dalla oro velocità al momento del lancio. Ma se prendo in considerazione che possono arrivare alla stessa distanza allora varia il tempo impiegato. Quello più veloce arriverà prima.
In pratica i due punti di vista dipendono solo dalla velocità ma non da due traiettorie diverse. Anche i due che partono da A per arrivare a B uno cortrendo e l' altro camminando. Entrambi arrivano a B solo in due tempi diversi ma seguendo copmunque la stessa traiettoria.
caro Rodolfo,
in questo momento il tempo mi è tiranno per motivi molto seri. Ti consiglio, comunque, queste "ciliegine", magari aiutano...
http://www.infinitoteatrodelcosmo.it/2020/10/03/lo-spaziotempo-e-la-nostra-prigione-quotidiana/
http://www.infinitoteatrodelcosmo.it/2020/10/10/ci-vuole-tempo-per-cadere/