Ho usato un metodo basato solo sulle forze, per non ripetere quello che usa i momenti come già correttamente spiegato da qualcuno di voi (bravi!). Non vorrei entrare in ulteriori complicazioni. Tra poco inserirò un nuovo quiz "papalliano", particolarmente divertente e leggermente più complicato. Il tempo mi sta un po’ scappando di mano e malgrado stia muovendomi sempre più velocemente continua a contrarsi… alla faccia della relatività ristretta!

Il problema di Ercole era schematizzato dalla figura dell’articolo e quindi si riferiva a una forza impartita in senso orizzontale passante per il centro di massa della sfera. Qualsiasi forza agente “fuori asse” comporterebbe l’introduzione di una rotazione della sfera attorno a un asse passante per il suo centro che niente avrebbe a che fare con la nostra situazione. Sarebbe sicuramente interessante studiare la dinamica di un sistema di questo genere così come quello in cui la forza, sempre passante per il centro, non fosse orizzontale. Nell’ultimo caso, teniamo presente che a noi non basta sollevare la sfera, ma dobbiamo spingerla in avanti superando lo scalino…

Mi sembra, perciò, inutile analizzare situazioni più complicate, proprio per il carattere didattico di questi “quiz”. Risolverlo nelle condizioni riportate nella figura è più che sufficiente per contribuire a una sempre maggiore dimestichezza con la meccanica classica. La prossima volta inserirò un quiz leggermente più complicato, ma non ingarbugliamo più del necessario ciò che vuole essere un esercizio di un certo livello di complessità. E, inoltre, non avrei tempo -adesso- di studiare in dettaglio situazioni alternative… abbiate pazienza!

Torniamo al nostro Ercole e alla situazione della Fig. 1. Come già avevo detto, esistono diversi modi per risolvere un problema dinamico e questo non è da meno. La soluzione più ovvia è quella già offerta da qualche lettore e che fa uso dei momenti delle forze in campo, ossia quella di Ercole e quella peso della sfera. Io, allora, lo risolvo in maniera leggermente diversa, facendo uso solo delle forze.

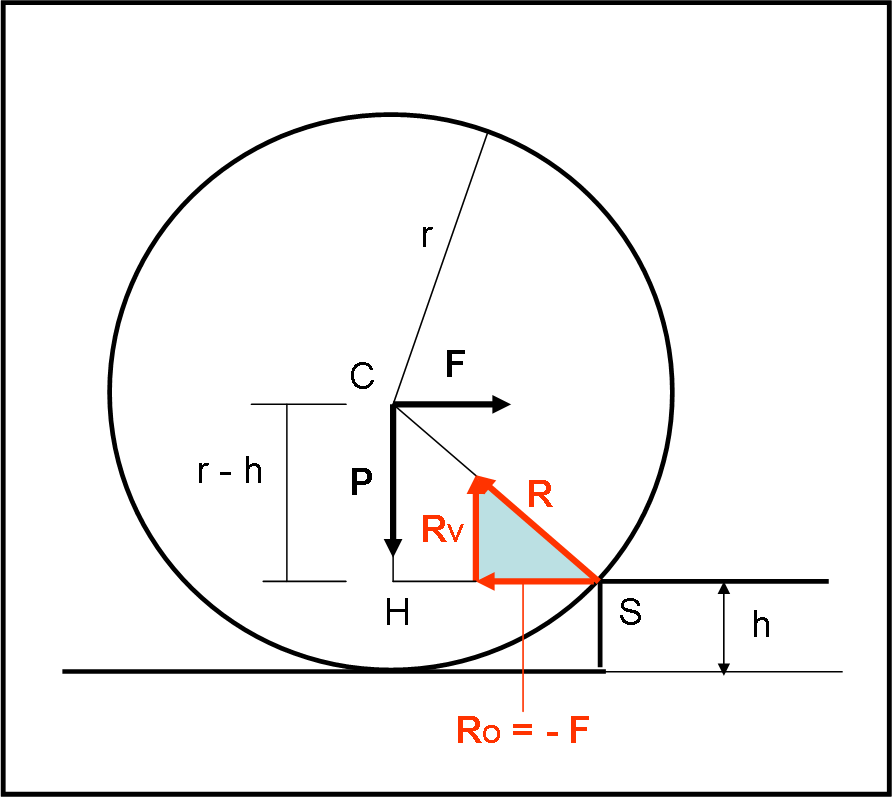
Una forza F orizzontale, agente su una sfera di peso P, comporta una reazione R applicata nel punto S (spigolo del gradino). Questa reazione ha una componente R_O parallela all’asse orizzontale e una verticale R_V. Aumentando la forza F la componente R_O deve rimanere sempre uguale a – F, dato che non vi è movimento. Per smuovere questa apparente apatia è necessario guardare l’altra componente della reazione, quella verticale R_V, diretta in verso opposto alla forza peso P. La sfera inizia a muoversi (ruotando attorno a S) quando R_V supera P. La forza F che smuove la sfera è quella che causa questa reazione verticale.

Non ci resta, quindi, che scrivere la relazione F/P che lega il rapporto tra F (variabile) e P (fissa).

Essa è descritta dal triangolo colorato in azzurro. Tuttavia, questo triangolo è simile a quello SCH che dipende solo dalla geometria del sistema. In questo triangolo si ha:

SC = r

CH = r – h

HS = ((r²) – (r – h)²)^1/2 = (r² – r² – h² + 2rh)^1/2 = (2hr – h²)^1/2 = (h(2r – h))^1/2

Da cui:

F/P = HS/CH = (h(2r – h))^1/2/(r –h)

E, infine:

F = P(h(2r – h))^1/2/(r –h)

Numericamente:

F = 500 x (1 x (6 –1))^1/2/(3 - 1) = 500 x (5)^1/2/2 = 559 kgp

Una sciocchezza per Ercole!