Questo articolo è stato inserito nell'approfondimento dedicato ai Buchi Neri, che raccoglie in modo organico gli articoli più significativi sull'argomento.

Questo articolo è una delle tante "ciliegine cosmiche" che potete gustare QUI

 

Spesso e volentieri, gli svarioni e le confusioni, che leggo nel web, mi spronano a cercare di chiarire fenomeni e concetti che non sono così semplici come probabilmente credevo. Mi dico sovente: “Gli esami non finiscono mai” e se si vuole compiere un’opera di buona divulgazione bisogna continuare a migliorarsi, con grande umiltà culturale. Ultimamente, mi sono reso conto che i buchi neri comportano problemi interpretativi che ingigantiscono quelli che in realtà possiedono. Se è meglio attendere prima di addentrarci nella problematica generale, cerchiamo, almeno, di eliminare eventuali fraintendimenti che troppo spesso vedo aleggiare nella rete, senza veder far molto, invece, per semplificare e chiarire…

Uno dei problemi più grandi che assillano molti “novizi” è quello relativo all’avvicinamento a un buco nero. Sicuramente, molte cose capitano e molte cose andranno spiegate con molta calma, dopo aver introdotto convenientemente la Relatività Generale. Tuttavia, buona parte dell’avvicinamento non pone assolutamente problemi speciali, almeno da un punto di vista teorico. In parole molto povere, possiamo dire che tutto si risolve pensando che l’unica cosa che fa differire una stella normale da un buco nero è solo e soltanto il suo raggio R. Alcune cose rimangono, infatti, inalterate, quali la massa M dell’astro e, di conseguenza, il campo gravitazionale che esso crea attorno a sé. Ciò che capita nei dintorni di una stella dipende, perciò, dalla distanza rispetto a lei, l'unica variabile in gioco.

Immaginiamo una stella S di raggio R, che se ne stia tranquilla nella sequenza principale. Ammettiamo anche che sia molto grande e che, quindi, la sua fine sarà catastrofica e darà luogo a una supernova e ciò che resterà di lei si ridurrà a un buco nero vero e proprio, capace di superare tutte le barriere che le particelle cercheranno di contrapporre alla pressione terrificante che tenderà a schiacciarla sempre più. Sto parlando degli elettroni e dei neutroni degeneri, quelli che permettono l’esistenza dei collassi parziali delle Nane Brune, delle Nane Bianche e delle Stelle di Neutroni. Ormai sappiamo bene, che queste difese sono dovute al nostro “amico” Pauli e al suo principio di esclusione. Ma lasciamo da parte la meccanica quantistica e anche i processi fisici che generano un buco nero e soffermiamoci solo su “ciò che si può fare” nei suoi dintorni. Come vi dicevo, niente di veramente strano capita realmente…

La Fig. 1 ci mostra una stella normale con il suo campo gravitazionale. In qualsiasi punto A, A₁, A₂ valgono le regole della meccanica classica (non abbiamo nemmeno bisogno di parlare di relatività generale). La massa M della stella è quella che è. La massa m degli eventuali corpi posti in A, A₁, A₂ poco importa, dato che siamo interessati al loro movimento, ossia a quanto sono accelerati dalla forza che agisce su di loro a causa di M (la sola forza presente). Sappiamo bene che l’accelerazione di gravità NON dipende dalla massa m e che è funzione della sola distanza r (variabile) del corpo A rispetto al centro della stella S (oltre, ovviamente, della massa M, che rimane, però, sempre la stessa). Oltretutto, possiamo sempre concentrare la massa della stella in un unico punto, detto baricentro (in questo caso C).

 

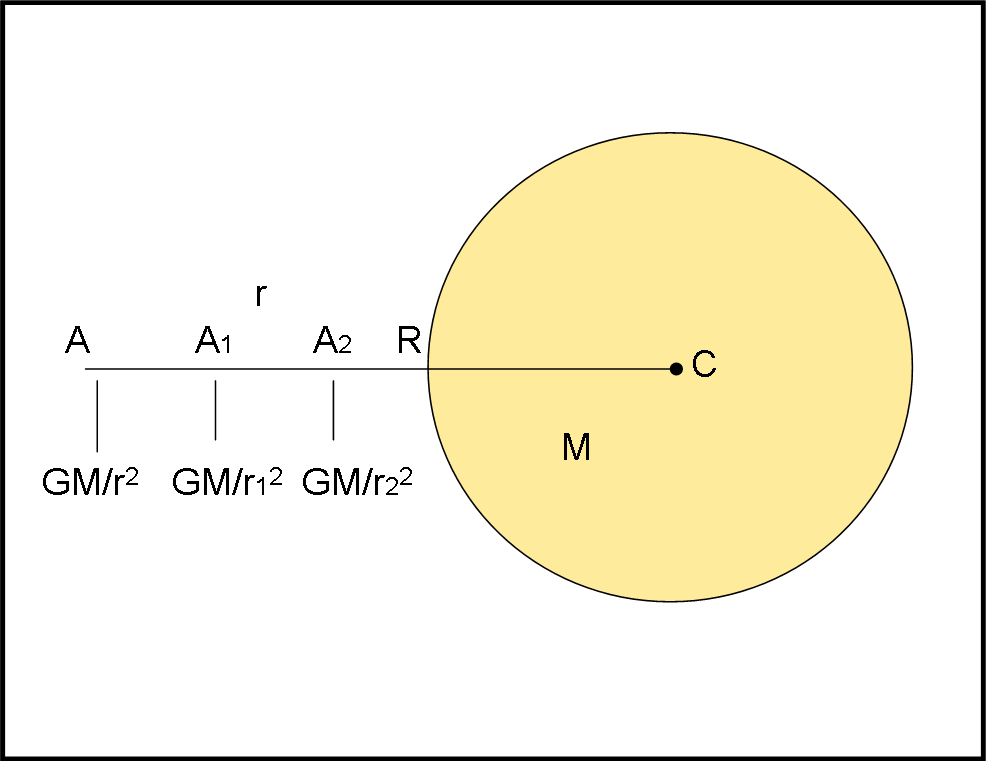
Che cosa blocca, allora, la posizione che può assumere A? Presto detto: la superficie della stella! Fino a una distanza R+ dR è sempre possibile, teoricamente, sapere con una formula di meccanica classica qual è la forza che agisce su di lei e , quindi, sempre teoricamente, calcolare che forza o -meglio- che accelerazione dobbiamo impartirle per farla tornare indietro, per farla scappare o per immetterla in orbita. Non si può andare oltre, solo e soltanto perché esiste la stella con la sua materia… E’ sempre il vecchio e risaputo problema della forza centripeta e della forza centrifuga, niente di meno e niente di più. Ciò che capita all’interno della stella S, a distanze minori di R, ha, invece, poco senso dinamico, dato che la fisica delle stelle prenderebbe il sopravvento.

In Fig. 2, facciamo l’esempio classico della Terra e del Sole (anche se il Sole non  potrà mai diventare un buco nero, noi lo costringeremo a farlo). Il nostro pianeta se ne sta tranquillo alla distanza r = a, dove la forza centrifuga è esattamente uguale e contraria alla forza centripeta, che in questo caso è proprio la forza di gravità del Sole. La Terra, in realtà, se vista da “fuori” gira intorno al Sole con la giusta velocità costante.

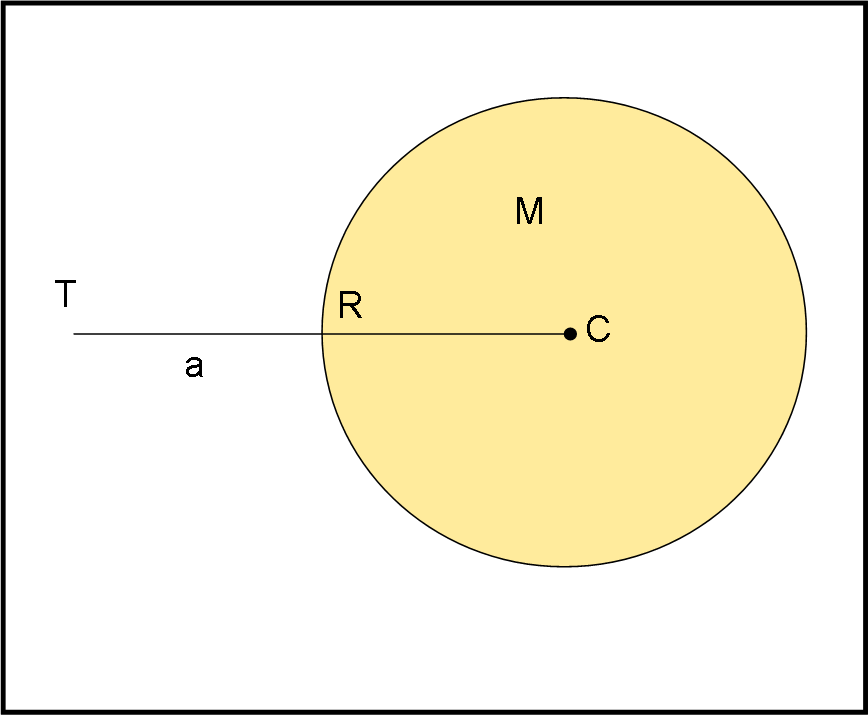
Tuttavia, chi sta su di lei si sente immobile ed è quindi costretto a “crearsi” una forza che controbilanci la gravità del Sole, ossia proprio quella centrifuga, odio e amore di tanti studenti (e non solo…). Noi, però, l’abbiamo sezionata e spiegata a lungo. Per quello che vogliamo discutere in questo articolo non ha molta importanza vedere dal di dentro o dal di fuori ciò che fa la Terra e possiamo trattarla come un corpo che rivolve attorno al Sole con una certa velocità, legata alla distanza dal centro della stella, l'unica variabile, dato che la massa del Sole, ovviamente, rimane costante. Potremmo spostare la Terra verso l’esterno o verso l’interno? Sicuramente sì, a patto di cambiarle la velocità. Sappiamo benissimo che esistono sia Venere che Mercurio, così come esistono sia Marte che Giove, e via dicendo.

Cosa comanda questo gioco di spostamenti orbitali? Solo e soltanto la massa del Sole (che rimane quella che è) e la distanza variabile del pianeta da esso. Qual è l’unico vincolo che limita un avvicinamento troppo stretto? Il fatto che la distanza r non può essere più piccola di R, se no si andrebbe arrosto.

Immaginiamo, adesso, di ridurre le dimensioni del Sole (Fig. 3), mantenendo però immutata la sua massa. Cambia forse il  campo gravitazionale? Assolutamente no, dato che la massa è quella che è. L’unica cosa che cambia è la possibilità di un pianeta di avvicinarsi ancora di più alla superficie del Sole. Abbiamo, infatti,  un nuovo raggio R₁, più piccolo di R. Teoricamente, perciò, potremmo portare un pianeta nella posizione T₁, dato che adesso non rischierebbe più di fondere completamente. Ovviamente, deve cambiare la sua velocità, per restare in orbita,  o -se preferite- deve cambiare la sua accelerazione centrifuga per controbilanciare un’accelerazione di gravità più grande: essa  aumenta solo perché è diminuita la distanza r.  In fondo niente di veramente eccezionale e il calcolo relativo rimane alquanto semplice e alla portata di tutti coloro che conoscono la meccanica classica.

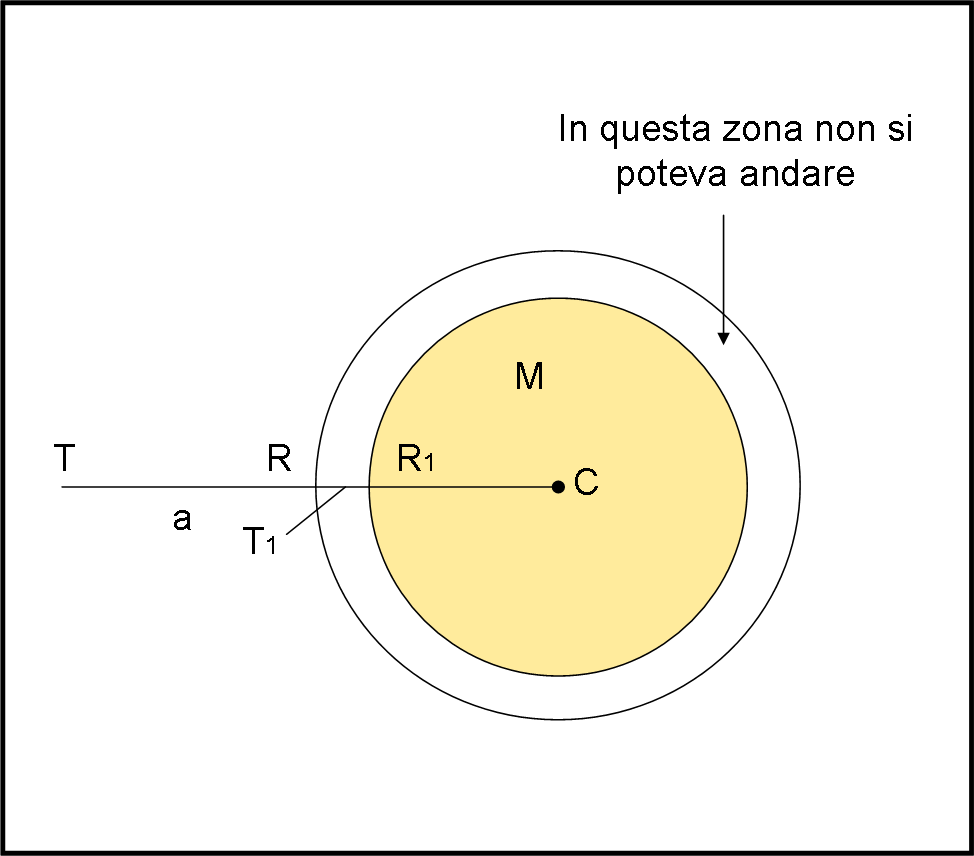
Ancora più facile è dire cosa capiterebbe alla “vecchia” Terra posta in T: niente di niente! Essa subirebbe sempre e comunque la stessa forza centripeta causata dal Sole e poco le importa che il raggio della stella sia passato da R a R₁. L’unica differenza (lo ribadiamo nuovamente) avviene nella corona circolare compresa tra R₁ e R. Questa è l’unica zona che prima non era percorribile da nessun corpo reale. Tuttavia, anche in quella zona era possibile calcolare, in via del tutto teorica, le orbite di eventuali corpi celesti. Orbite che non potevano esistere perché la zona era occupata dal Sole!

Ricordiamoci, ancora una volta, che la forza gravitazionale o il campo gravitazionale si calcola indipendentemente dal raggio della stella, ma solo in base alla sua massa M. Il fatto di ridurre il raggio vuol solo dire permettere uno spazio “utilizzabile” maggiore e quindi poter raggiungere distanze minori rispetto al centro del Sole. Sto dicendo banalità a raffica, ma temo che per alcuni queste considerazioni comportino ancora qualche problema concettuale e, quindi, voi che sapete, portate pazienza…

Continuiamo, comunque, a restringere il Sole, riducendo sempre più il suo raggio. A questo punto dobbiamo fare una semplice considerazione. La massa M rimane inalterata, mentre diminuisce il raggio. Se diminuisce il raggio, diminuisce anche il volume del Sole. Esiste una grandezza fisica molto importante che chiamiamo densità. Essa indica quanto è concentrata una certa massa ed è data dal semplice rapporto tra massa e volume occupato dalla massa. “Il volume di una sfera qual è? Quattro terzi pi greco erre tre!”. Chi non conosce questa specie di cantilena geometrica? Da lei deriva facilmente la densità ρ di una sfera di massa M:

ρ = M/(4/3 π R³)

dato che M, 4, 3, π sono costanti, possiamo concludere che la densità dipende solo dal raggio R raggiunto dal Sole. Quanto detto prima, può essere riscritto in funzione della densità: più cresce la densità della stella, maggiore è lo spazio disponibile affinché dei pianeti possano rivolvere sempre più vicini alla superficie del Sole. Si capisce benissimo che ciò che cambia questa possibilità “meccanica” può essere considerato solo in termini di densità della stella, dato che essa si lega immediatamente al raggio. Concetto, questo, estremamente banale, ma che a volte crea qualche confusione. La gravità in un certo punto è dovuta alla massa, ma i punti “liberi” in cui essa ha la possibilità pratica di agire dipendono solo dalla densità. Ecco perché per definire i buchi neri si usa quasi sempre la densità…

Tuttavia, pur continuando a ridurre il raggio del Sole e quindi ad aumentare la sua densità, la terra T si disinteressa completamente di ciò che sta succedendo alla sua stella. Nella sua posizione le formule restano sempre le stesse e anche il suo movimento: la massa e la distanza dal centro non sono cambiate.

Il Sole, comunque, come ogni oggetto celeste, nasconde, nel suo interno, un raggio particolare, che possiamo chiamare raggio di Schwarzschild (il raggio del celeberrimo orizzonte degli eventi), come rappresentato in Fig. 4 (le proporzioni non sono ovviamente mantenute).

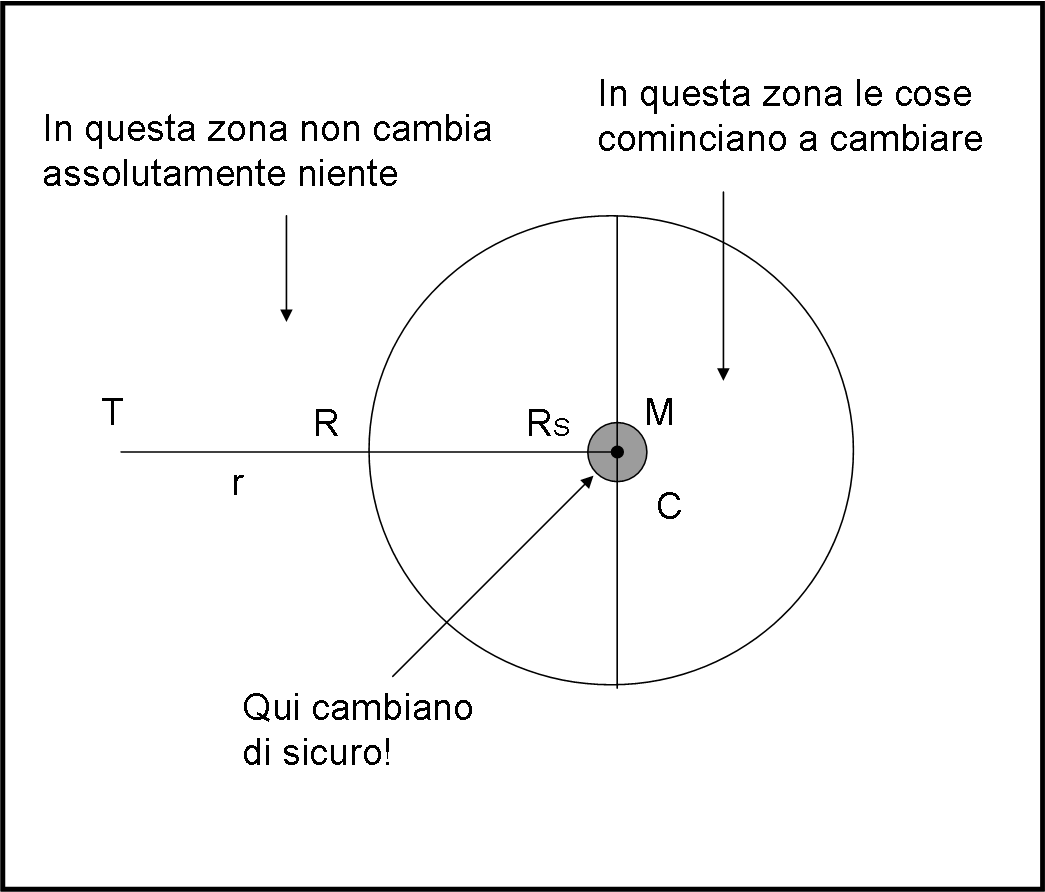
Questo raggio è tale che se la massa della stella si comprimesse al suo interno non sarebbe più possibile “scappare”, ossia non si potrebbe trovare una forza centrifuga che controbilanci la forza centripeta. O, alternativamente, non vi sarebbe una velocità minore di quella della luce che permetta a qualcosa di stare in orbita e ben poche "cose" possono raggiungere velocità di questo genere...

Nel caso del Sole questo raggio è pari a circa 3 km. Ne segue che per sentire gli effetti più macroscopici del Sole, ridotto a buco nero, bisognerebbe comprimerlo veramente tanto e andargli MOLTO vicini! A distanza di qualche milione di chilometri gli effetti rimangono ben poca cosa.

Non vogliamo ancora entrare in quella zona vicina ai tre chilometri da un Sole ultracompresso, dove ne capitano di tutti i colori. A noi basta concludere che i pianeti attuali, e anche qualcun altro inserito dove adesso non è possibile andare per le dimensioni solari, sono del tutto indifferenti al fatto che il Sole si contragga oppure no. E’, in fondo, la stessa cosa che capiterebbe se il Sole crescesse di raggio. La zona relativa alla sopravvivenza dei pianeti sarebbe vincolata alla nuova superficie. Tuttavia, chi è a distanza di sicurezza, come Giove e Saturno, non risentirebbe “meccanicamente” di questa espansione: il campo gravitazionale non cambierebbe.

Insomma, la nascita di un buco nero stellare cambia le cose solo all’interno della sua attuale superficie stellare e soprattutto quando ci si avvicina all’orizzonte degli eventi. Al di fuori di essa le cose rimangono assolutamente inalterate. Ribadiamo, quindi, ancora una volta, che se il Sole si trasformasse per magia in un buco nero inferiore ai 3 km di raggio, la Terra non risentirebbe di nessun cambiamento dinamico (ben diversi sarebbero gli effetti fisici dovuti all’energia prodotta da una stella che non è più una vera stella). Non avrebbe alcun problema a stare vicina a un buco nero! Tutti i giochini orbitali di avvicinamento e di allontanamento, se si restasse al di fuori dell’attuale superficie solare, sarebbero sempre possibili.

Orbitare attorno a un buco nero rimane un problema di meccanica elementare e non crea misteriose interazioni che tanto stimolano chi ha poco conoscenza del Cosmo. In altre parole, orbitare attorno a un buco nero oppure attorno alla stella che l’ha originato sono situazioni del tutto analoghe. Non vi è niente di speciale o misterioso. Non creiamoci misteri e complicazioni anche dove non ci sono: l’Universo ne ha già abbastanza!

Se vi è tutto chiaro, OK. In caso contrario non tacete e chiedete! C’è troppa confusione nel web e ben pochi che abbiano veramente voglia di spiegare (sempre che certe cose le abbiano capite veramente).

E’ meglio creare confusione, apparendo, però, superiore agli altri o è meglio semplificare, rischiando di apparire uno “normale”? Io preferisco nettamente la seconda soluzione… e invito tutti a seguire questa strada. Il giorno che parleremo di tensori (ad esempio) lo faremo solo se saremo in grado di spiegare e capire cosa siano realmente. Inserire nozioni non comprensibili, con molta alterigia, non serve a nessuno: né a chi dovrebbe recepirle, né -tanto meno- a chi le semina.