Ne avevamo parlato a lungo, ma giustamente si può anche tornare “a bomba” e vedere come sia le leggi del moto di Newton che lo sviluppo in serie possano risolvere il paradosso di Zenone, senza troppe parole.

Richiamiamolo rapidamente. Achille e una tartaruga fanno una gara di velocità. Sotto certe condizioni Zenone dimostra (a parole) che Achille non riuscirà mai a raggiungere la tartaruga, anche se la sua velocità è 10 volte superiore a quella della tartaruga. L’importante è che la tartaruga parta per prima. Zenone dice che Achille deve muoversi solo quando la tartaruga ha raggiunto i cento metri. In un attimo Achille percorre i cento metri, ma, in quel frattempo, la tartaruga si è portata più avanti di 10 metri. La tartaruga resta prima. Per Achille è immediato colmare anche lo svantaggio di dieci metri, ma la tartaruga è comunque riuscita di andare avanti di un metro. Anche se ogni volta il vantaggio della tartaruga diminuisce, essa resta sempre davanti ad Achille, che non riesce a raggiungerla MAI.

Il ragionamento è, ovviamente, sbagliato. L’errore sta nell’assumere che la somma di infiniti intervalli di tempo diano un risultato uguale a infinito. Ciò sarebbe vero se gli intervalli fossero sempre uguali o crescenti, ma non nel caso in cui ognuno di essi è più piccolo del precedente. In questo caso, ogni intervallo successivo è un infinitesimo di ordine superiore rispetto a quello precedente (ossia, è sempre più vicino allo zero) e la loro somma, anche se composta da infiniti termini, porta a un numero finito.

Lo possiamo risolvere perfettamente sia attraverso l’amico Newton sia attraverso un classico sviluppo in serie.

Consideriamo la legge oraria del moto di Achille, dove s_A è lo spazio percorso e v_A la velocità

s_A = v_At

L’origine dei tempi si ha quando Achille inizia la sua corsa. Infatti per t = 0, s_A = 0

Scriviamo, adesso, la legge oraria per la tartaruga:

s_T = v_Tt + s₀

Come voluto da Zenone, al momento della partenza di Achille (t = 0), la tartaruga si trova già nella posizione s₀ (che avevamo scelto essere 100 m).

E’ facilissimo mettere in grafico la situazione, dove l’ascissa è il tempo e l’ordinata è lo spazio percorso. I moti dei due contendenti sono rappresentati da rette. Sappiamo benissimo che la velocità è il coefficiente angolare di queste rette, per cui quella della tartaruga è inclinata dieci volte di meno di quella di Achille.  L’intersezione delle due rette indica sia il tempo t_I trascorso che lo spazio s_I percorso, nel momento in cui Achille raggiunge la tartaruga, come mostrato in Fig. 1.

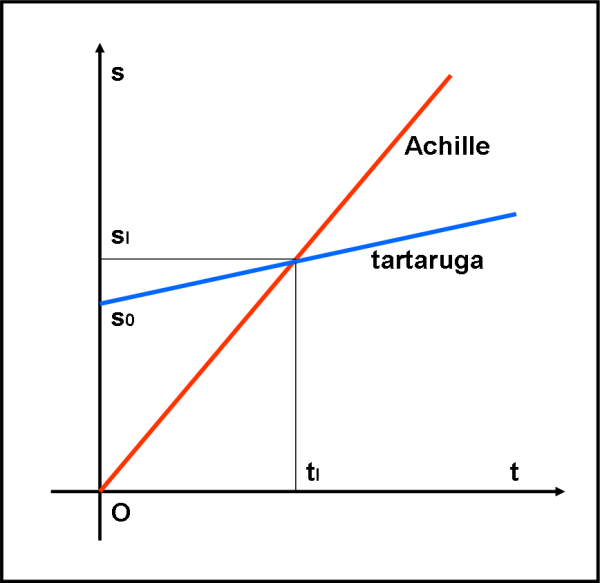
Graficamente, è un esercizio banale. Così come lo è anche attraverso la semplice relazione che si ottiene ponendo uguali i due spazi percorsi (al momento dell’incontro t_I, s_A e s_T DEVONO essere uguali a un certo valore s_I)

s_A = s_T = s_I

v_At_I =  v_Tt_I + s₀

Conoscendo le due velocità e lo spazio s₀, si ha subito il valore di t_I

t_I = s₀/(v_A – v_T)

E, immediatamente:

s_I = v_At_I = s₀v_A/(v_A – v_T)

Utilizziamo adesso quanto abbiamo imparato con le serie numeriche (N. 48 di approfondimenti di Matematica (cap. 39)). In particolare, andiamo a recuperare lo sviluppo in serie della funzione:

f(x) = 1/(1 – x)

Essa si scrive:

1/(1 – x) = 1 + x + x² + x³ + x⁴ + · · · = Σ^∞_n=0 xⁿ

E altro non è che la serie geometrica. Ricordiamoci che essa vale solo per -1< x < 1.

Torniamo ad Achille e alla tartaruga e ragioniamoci un po’ sopra.

Il tempo necessario ad Achille per percorrere il primo intervallo s₀ (dove era già arrivata la tartaruga al tempo t = 0) è dato da:

t₀ = s₀/v_A

In questo intervallo di tempo, però, la tartaruga ha proseguito di uno spazio s₁, che può essere scritto come:

s₁ = v_T t₀ = s₀ v_T /v_A

A questo punto, Achille deve percorrere lo spazio s₁ per cercare di raggiungere la tartaruga. Impiega un tempo t₁, dato da:

t₁ = s₁/v_A = s₀ v_T /v_A² = (s₀/v_A) v_T/v_A

Tuttavia, nel tempo t₁, la tartaruga è già andata avanti di un ulteriore spazio s₂, dato da:

s₂ = v_T t₁ = s₀ v_T² /v_A²

Accidenti! Achille deve perciò tentare di raggiungere lo stesso punto e impiega un tempo t₂, dato da:

t₂ = s₂/v_A = s₀ v_T² /v_A³ = (s₀/v_A) v_T²/v_A²

La storia, ovviamente, si ripete, ma non è difficile scrivere il termine ennesimo:

t_n = (s₀/v_A) v_Tⁿ/v_Aⁿ

Per trovare il tempo totale necessario ad Achille per raggiungere la tartaruga, non resta che sommare tutti gli intervalli di tempo ricavati precedentemente per n sempre più grande, ossia eseguire la somma:

t_I = t₀ + t₁ + t₂ + … + t_n + …

Possiamo tranquillamente fare andare n a infinito e scrivere:

t_I = Σ^∞_n=0 t_n

Ossia:

t_I = Σ^∞_n=0 t_n = Σ^∞_n=0 (s₀/v_A) v_Tⁿ/v_Aⁿ = (s₀/v_A) Σ^∞_n=0 (v_T/v_A)ⁿ

Ma questa non è altro che la serie geometrica che conosciamo molto bene (moltiplicata per una certa costante), in cui al posto di x è stato inserito v_T/v_A! Dato che -1 < v_T/v_A < 1, sappiamo benissimo quanto vale la sua somma:

1/(1 – x) = 1/(1 - v_T/v_A)

Benché la somma contenga un numero infinito di termini, il risultato è un numero finito.

In conclusione:

 t_I = (s₀/v_A)/(1 - v_T/v_A) = s₀ v_A/v_A(v_A – v_T) = s₀/(v_A – v_T)

Esattamente lo stesso risultato trovato seguendo la legge del moto di Newton.

Povera tartaruga, non ha nessuno scampo e viene raggiunta malgrado la furbizia  di Zenone.

Ringrazio Massimiliano e Umberto che hanno stimolato questo articolo!