Categorie: Fisica classica
Tags: forza centrifuga forza centripeta gravità Papalla quiz rotazione soluzione
Scritto da: Vincenzo Zappalà
Commenti:16
Soluzione del quiz sulla fermata di Papalla *
Le risposte sono state più che esaurienti. Tuttavia, può essere utile riassumere le idee ed evitare possibili confusioni tra moto orbitale attorno a Papalla e rotazione di Papalla. Facciamo anche qualche estrapolazione su larga scala. Ricordiamo, comunque, che bloccare istantaneamente la rotazione di un pianeta è un’ipotesi puramente fantascientifica.
Il quiz sull’improvvisa fermata della rotazione di Papalla merita qualche parola in più. Innanzitutto, evitiamo qualsiasi confusione tra la rotazione dell’intero pianeta e l’immissione in orbita di un oggetto attorno al pianeta.
Nel secondo caso è decisamente importante la massa del pianeta e il suo campo gravitazionale, dato che è proprio lui che regola la velocità orbitale.
Nel primo caso, poco importa che la Terra abbia una massa oppure no: quello che conta è che tutta la sua superficie ruoti attorno a un asse.
Usiamo altre parole. Nel secondo caso, il fatto che Papalla ruoti oppure no attorno al suo asse non ha alcuna importanza, dato che interessa soltanto inserire qualcosa in orbita attorno a lei. Per altezze diverse si avranno velocità diverse o -se preferite- oggetti che provengono con una certa velocità di crociera uniforme si inseriscono in orbita a diverse altezze.
In questo caso la forza centripeta è solo e soltanto la forza di gravitazione papalliana. Si può avere il caso limite di entrata in orbita ad un’altezza, rispetto alla superficie di Papalla, uguale a zero (sempre che non vi siano atmosfera, montagne, alberi o altri ostacoli…), ma questa orbita non ha niente a che fare con l'eventuale rotazione del pianeta.
Nel primo caso abbiamo, invece, un’enorme giostra sferica che ruota. Teoricamente potrebbe non avere alcuna massa al suo interno. Tutti gli oggetti che le sono posati sopra ruotano con lei. Possiamo anche vederla come una giostra in cui vi è un asse verticale (asse di rotazione) che ha una serie di corde di lunghezza decrescente dal centro verso l’alto e verso il basso a cui sono attaccati i vari oggetti che ruotano. Tutte le corde ruotano con la stessa velocità angolare. Ne consegue che più la corda è lunga e maggiore è la velocità tangenziale, che diventa zero quando si è ai due poli. In questo caso, ogni corda definisce una differente forza centripeta. Qualcosa di simile alla creazione di una gravità artificiale su una "ruota" spaziale.
La Fig. 1 illustra i due casi. In alto Papalla con la sua massa e con un satellite che orbita attorno a lei a un’altezza uguale a zero lungo un’orbita equatoriale (prima vista da un polo e poi equatorialmente). In basso, la giostra papalliana che ruota attorno all’asse di rotazione AR, anch’essa vista prima da un polo e poi lungo l’equatore.
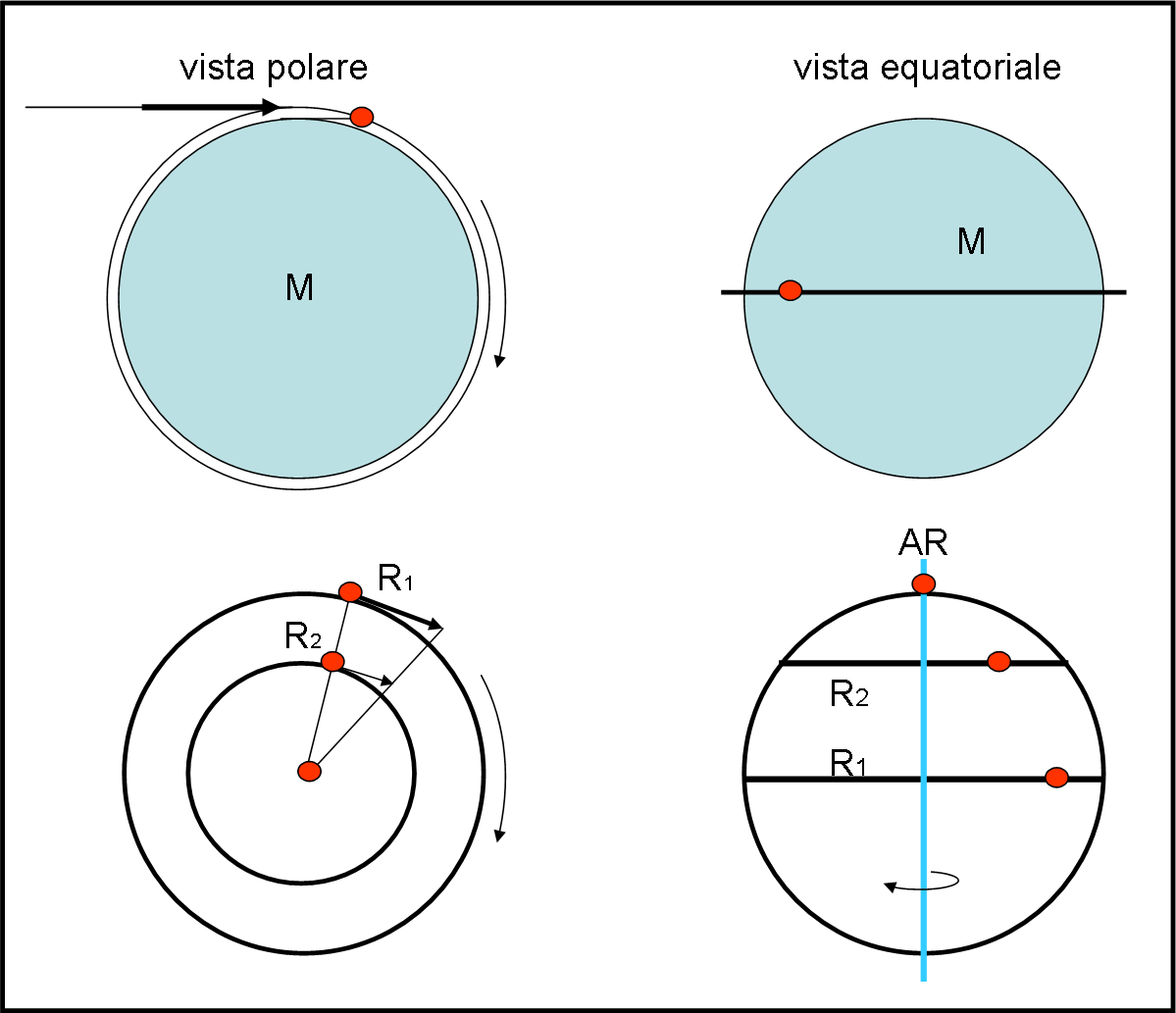
Abbiamo separato nettamente i due fenomeni per meglio discutere gli effetti una "fermata". In realtà, sappiamo che la forza centripeta introdotta con la rotazione va in qualche modo a combinarsi con la forza gravitazionale, giocando sul peso dei papalli.
Cosa vuol dire fermare la rotazione di Papalla? Beh… nel primo caso assolutamente niente, dato che il satellite percorre la sua orbita, bassissima, indipendentemente da cosa faccia il pianeta Papalla. Se fosse l’unico abitante di Papalla, non si accorgerebbe di niente.
Nel secondo caso, invece, fermare Papalla vorrebbe dire fermare la giostra o, se preferite, tagliare tutte le corde che legano i papalli all’asse di rotazione. Che ci sia o non ci sia un pianeta al centro della giostra, interessa relativamente poco.
TUTTI gli oggetti posati sulla giostra sferica viaggiano con una velocità, indipendentemente dalla loro massa, che varia passando dall’equatore (massima) verso i poli (zero). Fermando la giostra si elimina l’unica forza agente sui papalli, ossia quella centripeta; il primo principio della dinamica ci dice, allora, che i corpi continuano nel loro stato di quiete o di moto rettilineo uniforme. Quelli posizionati all’equatore continuano a muoversi lungo la tangente con un valore massimo della velocità, mentre quelli ai poli stanno perfettamente fermi.
A questo punto, però, entra in gioco la massa di Papalla e il suo campo gravitazionale. Ogni corpo in movimento lungo la tangente risente dell’accelerazione di gravità e tende a cadere verso il suolo. Esattamente ciò che capita a un proiettile sparato da un cannone.
La velocità tangenziale equatoriale, pur essendo molto grande, non riesce a mettere in orbita gli oggetti come nel primo caso. Siamo, infatti, ormai passati al primo caso, avendo oggetti che viaggiano a una certa velocità sotto l’effetto di un campo gravitazionale (che, se ruota o no, non importa più a nessuno).
Prima di proseguire, possiamo dire subito che, tra i due papallini, chi è stato più esatto nella risposta è stato il secondo (anche se si è riferito a “casa sua”).
Il primo papallino ha fatto un po’ di confusione… Se si ferma la rotazione, viene a mancare la forza centripeta (è come se si fosse tagliata la corda) e di conseguenza anche la centrifuga che gli era necessaria per sentirsi fermo nel suo sistema rotante. Ora, in balia del suo moto rettilineo uniforme, si sta semplicemente muovendo lungo una tangente alla sfera ormai immobile. In poche parole non esiste più il sistema solidale con la giostra rotante che lo vede andare in senso radiale. Ciò non toglie, tuttavia, che, esistendo un pianeta con la sua massa, anche se fermo, il moto rettilineo uniforme dura ben poco, in quanto viene subito deformato dall'accelerazione di gravità.
Il secondo papallino, invece, abita al polo per cui lui non ha mai subito alcuna velocità tangenziale (al limite girava su se stesso come l’asse di rotazione). Se l’asse di rotazione si ferma lui non acquista assolutamente una velocità tangenziale e non cambia posizione.
Potremmo fermarci qui… ma il quiz merita qualche parola in più relativamente alle conseguenze a breve e lungo termine. Anzi, ci sarebbe da scrivere un libro, anche se di scarso interesse fisico.
Un vero scienziato direbbe: “E’ un problema del tutto fantasioso che non può mai capitare e, quindi, è inutile parlarne. Al limite, si potrebbero studiare gli effetti di una rotazione che tende a zero su tempi lunghissimi, per effetti mareali…”.
Uno scienziato un po’ papalliano, come me, invece, accetta anche l’intervento di un PapalScherzone qualsiasi, aiutato da un PapalErcole, capace di bloccare la rotazione di Papalla, magari anche solo per un minuto.
Il primo scienziato avrebbe ragione, dato che per poter fermare bruscamente la rotazione di un pianeta come Papalla ci vorrebbe quasi sicuramente l’urto contro un oggetto di massa non molto diversa (è questione di annullare un momento angolare). Un tale urto non solo fermerebbe la rotazione, ma distruggerebbe l’intero pianeta… per cui la questione si chiude prima di iniziare.
Il secondo "scienziato" (?), pur accettando la situazione fantascientifica, è, comunque, costretto a farsi una domanda: “Dove finisce il pianeta e dove cominciano i papalli?”. In altre parole, quando si dice fermare il pianeta vuole dire fermare tutto ciò che è in qualche modo legato al pianeta o solo la parte fatta di roccia e terra. O ancora: un albero che è legato al pianeta attraverso le sue radici o un edificio che è ancorato saldamente attraverso le sue fondamenta alla roccia sottostante vanno considerati pianeta che si blocca o corpi che proseguono nel loro moto?
Pensiamo a una macchina che si ferma improvvisamente. Il guidatore (se non avesse la cintura) sfonderebbe il vetro (non fa parte della macchina). Ma se fosse un robot costruito insieme alla macchina si fermerebbe anche lui.
Ovviamente, a seconda dei limiti “teorici” dati al pianeta che si ferma, le conseguenze sono più o meno disastrose. Se alberi ed edifici restassero fermi, i papalli nel loro volo a grande velocità finirebbero sicuramente contro qualcuno di loro, prima di fermarsi grazie alla gravità papalliana.
Se, invece, gli edifici e gli alberi non si “fermassero”, riuscirebbero a sradicarsi e a crollare e le cose non sarebbero migliori…
Ovviamente, un discorso più serio dovrebbe tener conto degli attriti e dell’atmosfera (su Papalla non c’è, ma…). L’atmosfera viaggerebbe a grande velocità e si possono immaginare i suoi “impatti” contro le montagne e via dicendo. Per non parlare del mare che se ne andrebbe a zonzo. Insomma, uno scenario, comunque, terrificante. Chi vuole, può anche divertirsi a fare conti, ma anche uno scienziato un po’ papalliano deve limitarsi nel fare fantascienza catastrofica gratuita…
Ancora un accenno a un effetto sicuramente notevole che darebbe un brutto colpo al nostro papallino “polare”. La rotazione di Papalla fa sì che essa si “gonfi” verso l’equatore, ossia assuma la forma di un ellissoide schiacciato ai poli e allungato all’equatore.
Se si fermasse la rotazione, Papalla tenderebbe a diventare perfettamente sferica. Tuttavia, lungo la zona equatoriale gli oceani odierni si "prolungano" di qualche chilometro rispetto a una sfera perfetta. Quest’acqua tenderebbe, perciò, a ridistribuirsi sulla superficie e si creerebbe una zona emersa equatoriale simile a un unico enorme continente. I poli verrebbero sommersi e anche il nostro papallino finirebbe male…
Questa conseguenza è decisamente più “fisica”, perché si verificherebbe anche se Papalla si fermasse lentamente. QUI potete trovare informazioni più accurate
Non dimentichiamo, infine, che anche il campo magnetico potrebbe fermarsi, ossia sparire, se il nucleo non ruotasse. Niente campo magnetico, niente difesa contro i raggi cosmici…
Povera Papalla… continua a ruotare, non ti fermare!!!!!
P.S.: Non ne ho parlato apposta… potete calcolare da soli la velocità tangenziale all’equatore e la velocità necessaria per inserirsi in orbita a zero metri d’altezza. Vedrete che la differenza è piuttosto notevole.






16 commenti
Se qualcuno vuole provare a calcolare le due velocità all'equatore, dato che Papalla è simile alla Terra, volendo si possono usare questi dati..
La costante di gravitazione universale è uguale a:
La Massa di Papalla è: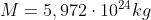
Il raggio misurato all'equatore è di:
Il periodo di rotazione del pianeta è:
Periodo (rotazione) = 23,9345 ore = 81 164,2 secondi
Quindi....
Paolo
@Paolo
I dati mi sembrano decisamente sovrabbondanti.
vt = velocità tangenziale all'equatore
Rt = raggio terrestre all'equatore = 6378 km circa
quindi vt =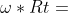 464 m/s = 1670 km/h circa
464 m/s = 1670 km/h circa
vf = velocità di fuga dalla Terra in superficie
un corpo in superficie riesce a sfuggire al campo gravitazionale della Terra se la sua energia cinetica uguaglia quella potenziale gravitazione sulla superficie, quindi:
da cui, semplificando m ed esplicitando rispetto a vf , si ottiene:
vf =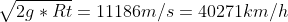 circa
circa
come si vede assai maggiore della vt.
Scusa Arturo ma la velocità di fuga consente ad un corpo di sfuggire alla gravità del Pianeta.. qui il corpo deve mettersi in orbita intorno al pianeta....
Paolo
Hai ragione Paolo, chissà per quale strano riflesso condizionato :-) , ho risposto pensando proprio alla velocità di fuga. In effetti, per stare in orbita teoricamente ad h=0 rispetto alla superficie terrestre , dovremmo uguagliare la forza centripeta con la forza peso:
dove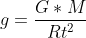 è l'accelerazione di gravità sulla superficie terrestre all'equatore.
è l'accelerazione di gravità sulla superficie terrestre all'equatore.
M è la massa terrestre e Rt il raggio terrestre all'equatore.
Anche qui, semplificando m ed esplicitando rispetto a v si ottiene, se non ho sbagliato i conti:
v = 7900 m/s = 28440 km/h
sempre assai maggiore della vt.
@ Michele, intendi dire che invece di M e G si poteva indicare il valore dell'accelerazione di gravità al suolo dell'equatore?
E' vero, ma oggi si tratta di Papalla domani di un pianeta con Massa o raggio diverso, per cui a mio avviso non fa male ricavare g.. non si sa mai...
Paolo
e bravi i miei colleghi e amici....
è un piacere con voi fare domande e poi mi aiutate un sacco
non mi ero mai posto il problema di mettere in orbita un satellite a distanza zero dalla superficie, ma senza componenti verticali della velocità non penso sia possibile.Nel nostro caso, anche se la velocità di rotazione fosse tale da generare una velocità tangenziale pari da eguagliare g in un moto circolare uniforme, bisogna pensare che quando il pianeta si ferma (anche istantaneamente) il corpo parte tangenzialmente con velocità Vt e descrive subito una parabola negli instanti successivi; la curvatura della parabola dipende d Vt e da g ma dovrebbe essere minore della curvatura del pianeta (in pratica anche se parte da un metro di altezza il corpo cade sul pianeta). Intendo dire che forse il calcolo di tale velocità è un pò più complesso.
caro Umberto,
ovviamente è un caso limite non "realistico", ma attraverso il calcolo delle velocità orbitale puoi benissimo ottenere il risultato voluto. Immagina pure di mettere la massa al centro... La vT è quella giusta per inserirsi in orbita, come per qualsiasi altra altezza. Non capisco perché non ti piace...
capisco che è quella giusta , ma a posteriori, pensando ad un orbita circolare. Io pensavo sopra a come si originava il fenomeno di messa in orbita, che all'inizio non è circolare, ma un moto parabolico
si... ho capito cosa intendi: il trasferimento orbitale, in poche parole. Ma qui dobbiamo considerare una velocità iniziale già perfetta...
si, adesso riesco a giustificarmelo; in pratica a quella velocità di rotazione la gravità viene annullata, quando si ferma il pianeta il moto non è parabolico ma circolare perchè c'è ancora compensazione perfetta fra g e la centrifuga. Diversamente avverrebbe per valori diversi di Vt; sarebbe inizialmente parabolico, vero?
direi di sì, Umberto... è proprio l'orbita di trasferimento più o meno classica. Pensa anche solo alla Terra di Newton con lui che tira le pietre. Sono tutte parabole fino a quella che diventa un cerchio. Se tiri dal livello del mare devi riuscire ad alzarti e quindi cominciare in modo parabolico...
sai che alla fine queste cose mi piacciono ancora di più della relatività? Veramente una bella storia che fa riflettere sulla precarietà del mondo in cui viviamo.so che Rubbia ha detto un giorno: Siamo su un treno che viaggia a (300?) Km/s ma la cosa peggiore è che ci siamo accorti che è senza macchinista
Partendo dalla domanda posta nell'articolo, ho realizzato due figure in stile papalliano..
Nella prima ci sono quattro papallini, che si trovano a latitudini diverse, tra questi uno si trova all'equatore e l'altro al Polo. Mentre Papalla ruota i papallini compiono un giro intorno al centro di rotazione.
Mentre ci si avvicina al polo, ogni papallino descrive una circonferenza sempre più piccola e conseguentemente anche la distanza r (raggio) dal centro di rotazione diminuisce, al punto che il Papallino al polo si trova proprio sul centro di rotazione (o meglio sull'asse di rotazione del pianeta), per cui non gira intorno a qualcosa, ma al limite ruota su se stesso.
Ovviamente ogni papallino avrà una conseguente velocità tangenziale diversa, come mostra la figura:
http://www.astrobin.com/full/235081/G/
Nel secondo caso invece ci sono due astronavi papalliane sferiche, una rossa e una blu. La prima gira intorno al pianeta all'altezza del suolo di Papalla (non ci sono montagne), seguendo la linea equatoriale...
La seconda gira intorno a Papalla ad una distanza dal suo centro di 80 000 Km e ad un altezza dal suolo di 1 621,8 Km.
In questo caso la distanza r è quella tra le astronavi e il centro di massa, ossia il centro del pianeta.
La forza di attrazione gravitazionale tende a trascinarle verso il centro del pianeta, esercitando sulle astronavi un'accelerazione centripeta, ossia diretta verso il centro del pianeta.
Nella figura ho provato a calcolare la velocità orbitale necessaria per contrastare l'accelerazione di gravità.
http://www.astrobin.com/full/235081/H/
Spero che le figure non contengano errori..
Paolo