QUIZ: una casetta nella sfera di vetro *
Questo è un quiz veramente semplice che, però, può essere risolto in vari modi. Inviterei i più giovani a provare senza paura, dato che -se vogliono- non hanno bisogno di nessuna formula…
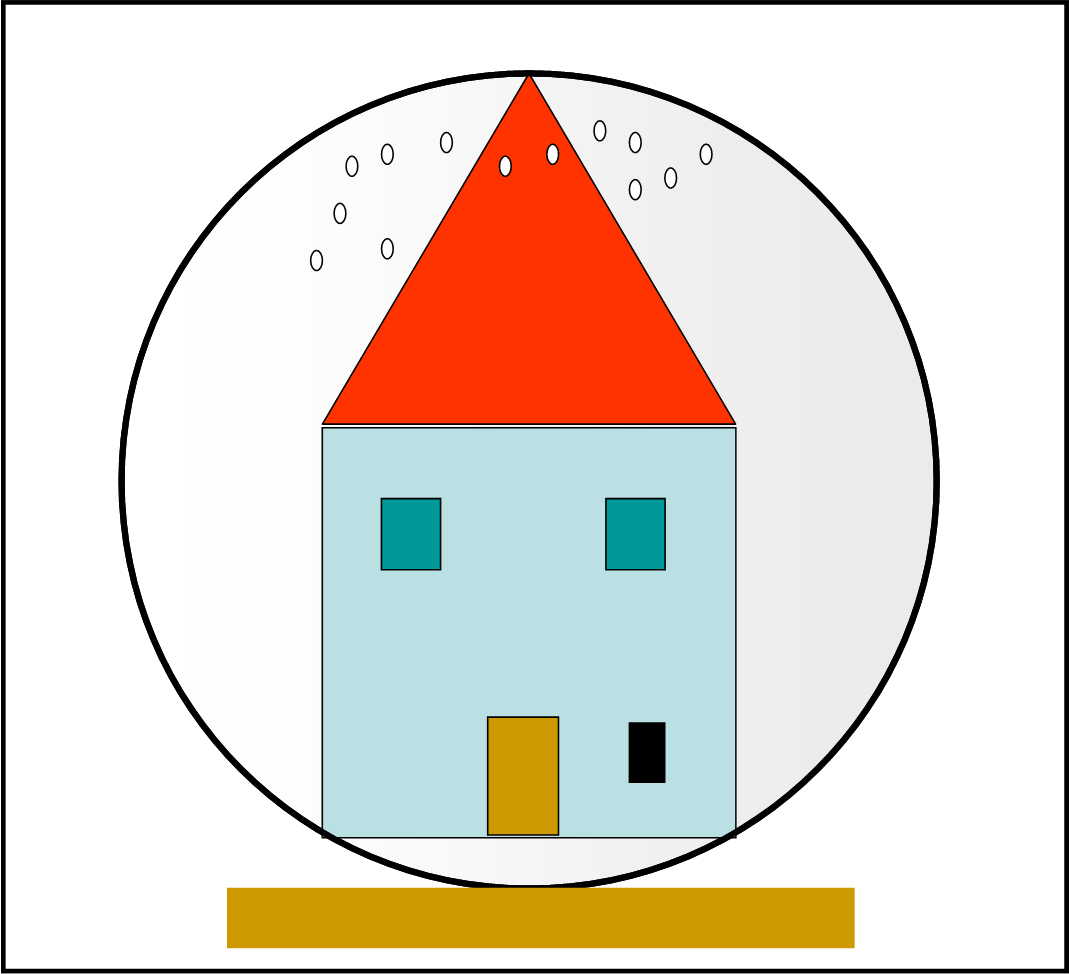
Un bimbo sta giocando allegramente con i cubetti a incastro che gli permettono di costruire case, palazzi, torri e tanti altri edifici. Alla fine, felice e contento, mostra ai genitori il suo piccolo capolavoro: una casetta con tanto di tetto, di finestre e di porta. Il lavoro è veramente ben fatto, anche perché usa forme decisamente semplici: la casa vera e propria ha sezione quadrata di lato uguale 10 cm. La sezione del tetto non è altro che un triangolo equilatero la cui base è nuovamente uguale a 10 cm. Proprio come descritto nella Fig.1.

Il papà decide che sarebbe bello conservare il piccolo capolavoro sotto vetro (con tanto di neve che scende… mamma mia, che gusto!) e alla fine ottiene ciò che mostra la Fig. 2. La domanda è banalissima: “Qual è il raggio della sfera di vetro che contiene perfettamente la casetta?”
Soluzione QUI





28 commenti
In caso posterò il mio ragionamento in un commento successivo
muble muble... io ci sarei arrivato senza l'uso di alcuna formula, però non mi sento più tanto giovane...
per cui, per ora mi astengo.
e aggiungo: ma certo che il nostro Prof tira fuori sempre dei quiz che, anche quando sono semplici, non sono mai banali e sono sempre intriganti
grazie Arturo... qualcosa si può sempre imparare...
Ci sono arrivato ma ho imbrogliato: ho usato l'autocad...
Sono curioso da vedere la soluzione. Uno dei modi credo sia ricavarlo dalla funzione del cerchio (i tre punti sono conosciuti, e per essi passa un solo cerchio), ma sinceramente non sarei piu' in grado... non risolvo equazioni da 25 anni...
nessuna equazione... solo qualche angolo...
Questo è il metodo molto "fai da te" che Valentina ed io abbiamo elaborato ieri sera.
Si disegna una casetta con le caratteristiche richieste e poi si prende un compasso: lo si punta in A con apertura AD e si ricava l'archetto rosso, poi lo si punta in B con apertura BC e ri ricava l'archetto verde. A questo punto abbiamo trovato l'ipotetico centro della circonferenza che deve contenere la casetta e lo verifichiamo puntando il compasso in O, infatti l'apertura coincide con OE.
Quindi OE=OA=OB=lato casetta=raggio della circonferenza
sarò buono... anche senza compasso... basta trascinare il tetto fino a farlo coincidere con la base della casetta... ;-)
mi piacerebbe , adesso, qualcosa di più ... matematico...
forza miei prodi (la gara è aperta a tutti!)
Ok, ok... ma sei stato tu a dire che non servivano formule e noi ti abbiano preso in parola!
sì, sì, hai ragione... ma ho soltanto chiesto un passetto in più... Paolo e Arturo scalpitano!!!!
Ciao Daniela,
io ho fatto piu' o meno lo stesso con autocad... ho disegnato un cerchio di raggio ED e ho notato che passava per il centro della bolla di vetro.
Ma cosi mi sa che non vale... in fondo la scelta di quel raggio e' arbitraria, funziona perché abbiamo scelto quello giusto. Credo che Enzo si aspetti qualcosa di piu' brillante... ;-)
Certo che si aspetta qualcosa di più brillante, lo conosco bene... ma credo che sarebbe questo l'unico metodo che un padre seguirebbe per realizzare un lavoretto fai-da-te e far divertire il figlio!
A proposito di metodi empirici e fai-da-te, Paolo S., guarda questo quiz: uno si scervella per capire come evitare un'irrisolvibile equazione a cinque o più incognite, cercando un modo matematico formalmente ineccepibile e generale per risolverlo... e poi bastava fare così!
Morale... neanche il nostro integerrimo Super-Mega-Prof. disdegna le scorciatoie!!!
Non era una scorciatoia, ma un metodo che corrispondeva esattamente alla domanda... E' stata scritta o no la formula ricorrente? Chi mai aveva detto di risolvere un'equazione in 5 incognite????
Povero me... ormai sono attaccato da tutti i fronti!!!!
Infatti anche il mio metodo corrisponde perfettamente alla domanda

al volo da una camera di albergo vicino Bologna , ma avevo salvato ieri l'immagine sul server per poterla linkare anche da qui con il tablet
la circonferenza deve passare per B, E ed A , il punto in basso a sinistra di cui pero' mi sono scordato di indicare la lettera. Per la simmetria della casetta, il centro O della circonferenza circoscritta non puo' che giacere sulla retta passante per E e perpendicolare alla base del quadrato. Consideriamo il punto O visibile nella figura come centro della circonferenza di cui pero' non conosciamo ancora il raggio. Consideriamo ora i due triangoli EOC e BOC. Essi sono congruenti perchè hanno i tre lati rispettivamente congruenti. Infatti risulta:
EO=OB perchè entrambi raggi di una stessa circonferenza
EC=BC per costruzione
OC in comune ai due triangoli
Essendo i due triangoli congruenti, allora risulta anche:
angolo EOC=angolo BOC (1)
Inoltre, considerando le rette parallele passanti rispettivamente per E,F e B,C tagliate dalla trasversale per O,C, risulta
angolo EOC=angolo BCO (2)
perchè angoli alterni interni.
Dalle (1) e (2) deriva quindi che:
angolo BOC=angolo BCO
Cioè il triangolo BOC è isoscele, quindi BO=BC. Dunque, il raggio della circonferenza circoscritta alla casetta è proprio uguale a 10.
Ma chissà se non c'è un altro modo (sempre senza fare uso di formule) per dimostrare la stessa cosa.
ottimo Arturo, ma penso ci sia qualcosa di più veloce... aspetto ancora un po'...
Ricordo: una cosa è trafficare con compassi e/o trasportare triangoli verso il basso (soluzioni PRATICHE) e un'altra è dimostrare teoricamente (senza formule) che il raggio deve essere uguale a 10 cm...
Forse con i gradi 60°x6?
Usando il trangolo equilatero i cui lati misurano 10 cm.... ottengo questa figura....
Il raggio del cerchio è uguale al lato del triangolo, ossia 10 cm..
Paolo
Ho letto la tua dimostrazione, Arturo, e non mi torna una cosa, sicuramente c’è qualcosa che mi sfugge e vorrei capire.
Tu inizi dicendo che i triangoli EOC e BOC sono congruenti perché hanno tre lati uguali: OC è in comune, CB=CE per costruzione e fin qui ci siamo; poi dici che OB=OE, ma non è quello che vogliamo dimostrare? Non comprendo con quale criterio sia stato scelto il punto O.
Stavo pensando che forse si potrebbe partire tracciando BO parallela a EC (troviamo O ma ancora non sappiamo se OE=OB), dimostrare che i triangoli sono congruenti perché hanno due angoli uguali (ECO=BOC e EOC=BCO alterni interni) e il lato OC tra essi compreso (2° criterio), quindi OB=OE… per poi dimostrare, come hai fatto tu, che i due triangoli sono anche isosceli e quindi il raggio della circonferenza è uguale al lato della casetta.
Dove sto sbagliando? Perché sicuramente sbaglio io...
al volo da casa di parenti qui a Verona (e lo so, in questi giorni sono in giro )
)
Daniela, OB = OE perchè entrambi raggi (di misura inizialmente ignota) di una stessa circonferenza (ossia quella passante per i punti A, B ed E). Cioè, se prendo due qualsiasi raggi di una stessa circonferenza , hanno necessariamente la stessa misura. Quello che si deve dimostrare è che il raggio è uguale al lato del quadrato.
Ok, grazie Arturo!
Aggiungo un approccio un pò più geometrico e ragionato... ho provato a uasre i triangoli equilateri per approssimare una circonferenza...
Paolo
sempre con considerazooni relative alle coppie di rette parallele (le indico con o due punti per cui passano) EF-CB ed EC-OB (quest'ultima ottenuta traslando in basso la retta EC, si ottiene che gli angoli EOB ed ECB sono congruenti. Allora EOBC e' necessariamente un rombo, quindi i suoi quattro lati sono uguali . Quindi il raggio (lato EO oppue lato OB) è uguale a 10.
(E' un rombo perchè è anche, per costruzione, EC=CB.
pero' in questo caso credo che si dia per scontato che il punto O ottenuto qui traslando in basso la retta EC sia il centro della circonferenza circoscritta alla casetta. Quindi, mi sa che questa non sia una valida alternativa.
Ieri appena dopo pranzo, avevo provato con l’esagono da inserire nel primo disegno di paolo, si dovrebbe riuscire a dimostrare che la punta del tetto è uguale al triangolo celeste al centro.
Chiedo scusa Paolo.