QUIZ: affettiamo un triangolo ***
Questo quiz potrebbe apparire semplice. In effetti, per risolverlo, sono necessari pochi rudimenti di matematica elementare. Tuttavia, può dare luogo a varie possibilità, che possono cambiare da caso a caso. Via, quindi, con la soluzione più semplice, ma via anche con alcune considerazioni meno immediate…
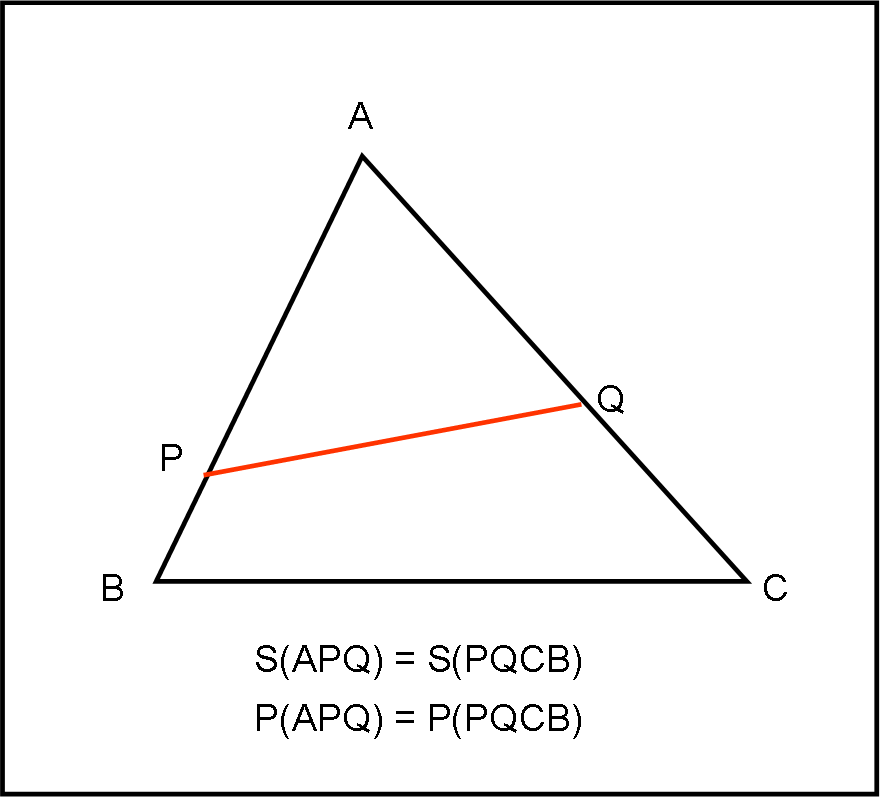
Prendiamo un triangolo qualsiasi e cerchiamo di trovare un segmento “equalizzatore”, ossia che sia in grado di dividerlo in due parti che abbiano sia la stessa area che lo stesso perimetro. Qualcosa come quello che è rappresentato nella figura che segue.
Forza, trovate questo segmento (definendolo perfettamente rispetto al triangolo) e cercate anche di vedere se ne esiste uno solo o più di uno…
Buon divertimento e non andate a tentativi, ma trovate le soluzioni con relazioni matematiche.
Soluzione QUI.
12 commenti
Siano dati u,v,z i lati del trianglo ABC.
Siano invece x,y,w i lati corrispondenti del triangolo APQ
siano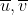
due vettori di modulo u e v corrispondenti a AB e AC che formano un angolo 
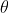nel vertice A.
Analogamente siano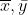
i due vettori corrispondenti ai lati AP ed AQ.
Possiamo scrivere i due prodotti vettoriali
ma noi sappiamo che il prodotto vettoriale esprime l'area orientata del parallelepipedo compreso fra i vettori , che è geometricamente il doppio delle aree ABC e APQ.
Quindi tenendo conto che l'area di ABC è il doppio di quelle di APQ e semplificando :
u v = 2 x y .
Passiamo ai perimetri:
Perimetro APQ = x + y + w
Perimetro PQCB = u-x+v-y+w+z
Ugugliando e semplificando
x+y= 1/2(u+v+z) =Perimetro di ABC = P/2 (noto in quanto conosciamo u,v e z)
in sintesi abbiamo
x+y= P/2
xy = u v /2
m noi sappiamo che la somma delle radici di una equazione di secondo grado normlizzata è il coefficiante -b, mentre il prodtto è il coefficiente c.
Possaimo quindi scrivere l'equazione:
che risolta fornisce i valori x e y, lati superiori del triangolo APQ in funzione dei valori noti u,v,z lati del triangolo maggiore ABC.
Sarei grato a chi mi fa un esempio numerico .....
Forse esiste anche un metodo grafico ma non riesco a farlo.
Per me idem come Leandro, salvo che per trovare l'area del triangolo, noti due lati e l'angolo compreso, applico direttamente la formula della trigonometria, secondo cui, appunto, l'area è pari al semiprodotto delle misure dei due lati per il seno dell'angolo compreso.
un po' di discussione su quante soluzioni esistono ... e alcuni casi particolari... ?
E intanto scriviamo le soluzioni...
Arrivo circa alle stesse conclusioni di Leandro ed Arturo Lorenzo, aggiungerei solo le condizioni di validità delle soluzioni trovate.
Algebricamente esistono 6 modi diversi per posizionare P e Q, 2 per ciascuna coppia di lati, ma non tutti sono geometricamente validi, cioè con P e Q all'interno dei lati del triangolo.
Se indico con x ed y i rapporti AP/AC e AQ/AB e p il perimetro di ABC, le soluzioni per il posizionamento di P e Q sui lati AC, di lunghezza a, e AB, di lunghezza b, sono:
Per essere valide occorre che siano raeli, cioè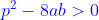 che
e che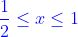 
. affinchè i punti P e Q siano interni ai segmenti AC e AB.
Casi particolari sono i triangoli equilatori ed isoscele. Nei triangoli equilateri sono soluzioni valide le tre mediane.
Algebricamente^2-8&space;a^2}}{4a}=\frac{3a\pm&space;a}{4a})
che ha come soluzione (x=1,y=1/2) e (x=1/2, y=1), cioè uno dei punti P o Q posto su un vertice e l'altro sul punto medio del lato opposto. Le soluzioni valide sono 6, ma a 2 a 2 uguali.
Discorso analogo vale per il triangolo isoscele, una soluzione è la mediana tra i lati uguali.
In caso di triangolo scaleno non sono riuscito ancora a trovare una regola generale.
Sembra che per i triangoli scaleni con un lato molto più piccolo degli altri ci sia una sola soluzione valida che taglia il lato più corto e quello più lungo. Ad esempio a=4, b=10, c=7, la sola soluzione valida è (x=0,8,y=0,625). Per quelli con lati meno diseguali possono esserci più soluzioni.
Il procedimento che ho seguito è questo.
Il quiz indica due condizioni: quella sull'area e quello sul perimetro.
Cerco di metterle in relazione con 2 incognite. Quelle più evidenti mi sembrano essere le lunghezze dei due segmenti AP e AQ, che esprimo come rapporto con i relativi segmenti interi AC e AB. Chiamo questi rapporti, che saranno le mie incognite, x ed y.
Per comodità di scrittura delle formule chiamo AC=a, AB=b, BC=c, AP/AC=x e AQ/AB=y.
Se A è l'area del triangolo completo, è voglio dividerlo in due parti di area uguali, ciascuna delle parti deve avere area metà della totale: quindi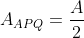
.
Per calcolare l'area del triangolo occorre conoscere una base e la relativa altezza. Se prendo come base b l'altezza sarà CN che chiamo h e quella del triangolo APQ sarà PM.
I triangoli APM e ACN sono simili poiché sono retti ed hanno un angolo in comune, quindi PM/CN=AP/AC=x e CM=x h
Quindi posso scriver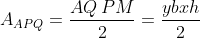e
e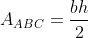 
,
poichè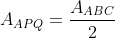
ne segue che
La relazione sulla uguaglianza dei perimetri è:
AP+AQ+PQ=PQ+PC+QB+BC
PQ è in comune nelle due figure e quindi scompare dalla equazione, rimane quindi:
x a+y b=(1-x) a+(1-y) b+c
ed questa è la relazione che garantisce la condizione sui perimetri.
Riassumendo devono valere le due relazioni:
1)
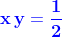
2)
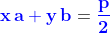
Estraggo y dalla prima e lo sostituisco nella seconda:
1)
2)
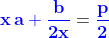
Minimo comune denominatore della seconda e porto tutto a sinistra nell'ordine solito delle equazioni di secondo grado.
che ha come soluzioni
dalla quale si può ricavare che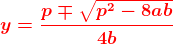 
Quindi ci sarebbero in totale 6 soluzioni possibili, 2 per ciascuna coppia di lati sui quali inserire i punti P e Q, ma non tutte queste soluzioni sono valide poiché P e Q devono essere all'interno dei lati.
Per estrarre le soluzioni valide occorre aggiungere due ulteriori condizioni.
x deve essere reale, cio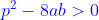è
e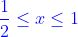 
affinchè i punti P e Q siano interni ai segmenti AC e AB.
Non è necessario aggiungere condizioni su y poichè quelle su x già garantiscono le stesse condizioni anche per y.
ancora una volta siete stati bravissimi. A questo punto, devo ammettere che anch'io sono alla ricerca di un metodo per valutare il numero di soluzioni reali (sono veramente sei oppure no?). Fabrizio ha preso una strada ottima... ci provo anch'io, appena ho tempo. Ovviamente, siamo ben oltre quanto richiesto... Ma, proviamo a fare un passo in più... Vi comunico che non è cosa semplice, dato che ci sono ancora dispute a riguardo...
Comunque che gruppo abbiamo qua dentro!!!!
(non lo ammetterà mai, dato che le ho dato un aiutino insignificante), ma c'è riuscita anche Daniela... bravissima anche lei... E spero che ne arrivino altri (normalmente nessuno legge la soluzione senza prima provare... )
caro Fabrizio,
in realtà sembra proprio che non ci possano essere più di tre soluzioni (assumendo come una sola soluzione due soluzioni uguali).
La trattazione generale è piuttosto faticosa, ma si può trovare... assumendo a<=b<=c. Si costruisce una certa relazione che a seconda se è negativa, nulla o positiva porta a 1,2 o 3 soluzioni... Un lavoraccio, però... non pretendo tanto... ma voi siete così bravi che...
caro Vincenzo,
per come l'hai messa non potevo non provarci.
Forse ci sono. Effettivamente è bella lunga, anche se non sempre ho utilizzato argomenti formali. Ho cercato di inserire alcune figure che questa sera sto completando. Spero di caricare il tutto domani.
Fabrizio
caro Fabri... ti inviteranno alle olimpiadi di matematica.... mi vergogno quasi a proporti quiz troppo facili! Comunque, che piacere trattare con persone come voi!!!!! Senza, però, diminuire il valore di tutti quelli che ci seguono e che cercano di acquisire una visione della fisica e dell'astrofisica sempre più generale. Il Circolo merita ormai la C maiuscola! Sono ultra preso con la doppia ragnatela...a furia di aggiungere sto scrivendo un testo di meccanica...
Se a,b,c sono i lati del triangolo, data l'equazione di secondo grado risolutiva
per avere soluzioni reali si impone il determinante maggiore di zero:
che sviluppata fornisce l'equazione omogenea di una iperbole
senza perdita di generalità possiamo porre c=1
le possibili soluzioni sono contenute nella parte interna del quadrante positivo degli assi x y
compresi dentro l' iperbole
e dal vincolo geometrico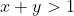
(cioè si deve formare un triangolo reale).
bravo Leandro!!!!! ottima deduzione...
Questo è il mio tentativo di trovare quale è la relazione tra i lati di un triangolo scaleno che permette di indicare quanti segmenti equalizzatori possono essere tracciti su quel triangolo.
Se il ragionamento che ho seguito è corretto, questo numero dipende dal segno di questa relazione:
dove s è il rapporto tra la lunghezza del lato più corto e quello più lungo ed m è il rapporto tra la lunghezza del lato intermedio e quella del più lungo.
Se per il triangolo scaleno considerato il valore della relazione è:
Un modo è sempre tra lato più lungo e lato più corto. Gli altri, se ci sono, sono tra lato più lungo e lato intermedio.
Faccio un esempio con un triangolo con lati di lunghezza a=10, b=7 e c=4.
Quindi s=0,4 m=0,7 e
Quindi avrebbe un solo segmento equalizzatore posizionato tra i lati a e c. In particolare quello sul lato a è di lunghezza 8 e quello sul lato c di lunghezza 2,5.
Se invece il triangolo avesse i lati a=10, b=9 e c=8 ci sarebbero 3 segmenti equalizzatori poiché per s=0,8 e m=0,9 e quindi
Il ragionamento che mi ha portato a queste conclusioni si basa su tre congetture trovate smanettando con diversi triangoli scaleni:
Se dimostro queste tre congetture si potrebbe affermare che in ogni triangolo scaleno ci possono essere da 1 a 3 modi diversi di posizionare PQ, gli estremi di un segmento equalizzatore. Il numero dipende se ci sono e quanti sono i modi di posizionare PQ tra il lato più lungo e quello di lunghezza intermedia del triangolo.
In realtà, la dimostrazione delle tre congetture non porterebbe alla condizione che ho scritto sopra. Fortunatamente, nel corso del ragionamento, mi sono imbattuto in un altra proprietà delle soluzioni del terzo caso che permette di restringere l'espressione a quella scritta.
Questo è il ragionamento che ho seguito per giungere a queste conclusioni.
Non è una vera dimostrazione poiché il procedimento in alcuni passaggi fa intervenire l'inuito visivo, ma credo possa essere abbastanza convincente, sempre che sia corretto.
Prima di affrontare le tre congetture preparo gli strumenti necessari.
Affinché PQ sia un segmento equalizzatore devono valere queste condizioni su x e y:
Traduco geometricamente queste condizioni in figura:
Quindi ci possono essere rette (rosse in figura) che non intersecano la curva blu e la intersecano in un punto non valido, fuori del quadrato verde. Quindi in quel triangolo non è possibile posizionare alcun segmento PQ tra i lati che definiscono la retta.
Rette (verdi in figura) che intersecano una volta la curva blu all'interno dell'area valida, dalle quali si può ricavare il posizionamento di un segmento PQ.
Rette (gialle in figura) che intersecano la curva blu in due punti nell'area valida, dalle quali si può ricavare il posizionamento di 2 segmenti PQ.
Per trovare la validità delle soluzioni, quindi dovrò verificare la posizione della retta rispetto al quadrato verde ed alla curva blu. Per questo userò i valori assunti da y per x=0,5 e x=1:
Non servono le lunghezze assolute dei lati perchè i risultati sulla posizione di segmenti equalizzatori trovati per un triangolo si possono trasferire a tutti i suoi triangoli simili, quindi contano solo i rapporti tra i lati.
Ci sono dei limiti ai valori di s e m che torneranno comodi nei ragionamenti successivi:
s<m<1, 1-v<s<m e 0,5<m<1.
Che s e m siano minori di 1 e che s<m credo sia chiaro dalla definizione.
m>0,5 perchè s+m>1 (un lato di un triangolo deve essere maggiore della somma degli altri due altrimenti il triangolo non si può chiudere) e se m fosse minore di 0,5 allora s<m non potrebbe valere. 1-m<s è solo un modo diverso di scrivere s+m>1.
A questo punto passo alle mie congetture.
Perchè non è possibile posizionare il segmento PQ tra i due lati più corti del triangolo.
In questo caso posso assumere a=s, b=m e c=1, quindi l'equazione 2 può essere scritta come
Mi interessa capire dove passa questa retta rispetto al quadrato verde dell'area ammessa.
Per questo calcolo i valori di y per x a 0,5 e 1.
Osservo che al crescere di m, y diminuisce. Poiché 0,5<m<1 allora, se inserisco il valore minore di m (0,5) ottengo il valore più grande di y e se inserisco il valore più grande di m (1) ottengo il valore più piccolo di y cioè:
1<y(0,5)<1,5. Riporto nella prossima figura questo intervallo, barra gialla a sinistra.
Anche qui al crescere di m ed s il valore di y cala. Quindi il massimo di y(1) si ottiene quando s e m sono i minimi possibile cioè s=1-m e m=0,5, ed il minimo quando s e m sono massimi, cioè: s=m e m=1:
Quindi 0,5<y(1)<1 che riporto in figura, barra gialla a destra.
Le rette relative al caso che esaminiamo sono decrescenti e devono passare allinterno delle due barre gialle.
Osservando la figura si vede che una retta che passa all'interno delle barre gialle non può incontrare la curva blu nella zona ammessa. Al più lo fa la retta agli estremi, che però non è una retta valida perchè le disuguaglianze viste sopra non ammettono l'uguale.
Così credo di avere dimostrato che non ci sono segmenti equalizzatori tra i due lati più corti.
Passo alla seconda congettura.
Perché il segmento PQ può essere sempre posizionato in uno ed un solo modo tra il lato più lungo ed il lato più corto
Il procedimento è simile al precedente.
In questo caso a=s, b=1, c=m, quindi l'equazione 2 può essere scritta così:
I valori che y può assumere per x=0,5 e x=1 sono:
0,75<y(0,5)<1, intervallo che riporto nella prossima figura con la solita barra gialla a sinistra
Per trovare il minimo devo inserire il massimo di s (1-m) ed il minimo di m (0,5) e per trovare il massimo inserisco il minimo di s (1-m) ed il massimo di m (1):
0,5<y(1)<1, che riporto in figura con la barra gialla a destra
Così credo di avere dimostrato che c'è sempre uno ed un solo segmento equalizzatore tra lato più lungo e lato più corto.
Passo all'ultima congettura.
Perchè tra il lato più lungo e quello medio ci sono casi nei quali non c'è modo di posizionare PQ, altri nei quali ci sono 2 modi diversi, altri nei quali c'è un solo modo (o due modi coincidenti)
Solito procedimento.
In questo caso a=m, b=1, c=s, quindi l'equazione 2 può essere scritta così:
Vediamo dove può passare questa retta.
0,5<y(0,5)<1, che riporto in figura con la solita barra gialla a sinistra
0<y(1)<0,5 che riporto in figura con la barra gialla a destra
Con questo credo di avere dimostrato la terza congettura.
C'è però un'altra informazione importante che posso dedurre dalla figura senza la quale sarebbe molto più difficile trovare la condizione che distingue i tre casi.
Le intersezioni tra le rette e la curva blu avvengono tutte all'interno del quadrato verde, cioè se ci sono soluzioni reali sono tutte valide.
Mi posso quindi concentrare solo sul caso di segmento equalizzatore tra lato più lungo e lato intermedio e trovare quante soluzioni reali presenta il sistema tra le equazioni 1 e 2 per un certo triangolo, tanto sono tutte valide.
Nel caso che analizzo ora a=m, b=1 e c=s
1)
2)
Si può eliminare y tra le due ed ottenere
Come per tutte le equazioni di 2° grado, il numero di soluzioni reali che può avere è indicato dal segno del discriminate:
che può essere espanso in
Poiché il secondo fattore è sempre positivo, il segno dipende solo dal primo, quindi è equivalente analizzare
o 
che se positivi indicano la presenza di 2 soluzioni reali, se nulli di una soluzione reale e se negativi di nessuna soluzione reale.
Queste soluzioni si aggiungono a quella sempre presente tra il lato più corto ed il lato più lungo.
Quindi un triangolo scaleno può avere da 1 a 3 segmenti equalizzatori a secondo del segno negativo, nullo o positivo delle espressioni indicate sopra.
Con questo credo di avere dimostrato, almeno intuitivamente, quanto anticipato all'inizio, a meno di errori.
cari Fabrizio e Leandro,
avete fatto un lavoro encomiabile (che ovviamente va oltre quanto richiesto dal quiz e che molti lettori potevano affrontare). La soluzione definitiva è ancora frutto di discussioni tra i matematici... Quando pubblicherò la soluzione, limitata alla parte per i "comuni" mortali, inserirò anche un link a una serie di teoremi che portano alla vostra conclusione e potrete controllare i vari passaggi... OK?
Vi ringrazio ancora di vero cuore!