Come già accennato, mentre è abbastanza semplice riuscire a trovare il modo per “affettare” il nostro triangolo, è molto meno intuitivo valutare quante siano in realtà le possibilità di farlo. Esse dipendono dal tipo di triangolo e necessitano di ragionamenti piuttosto elaborati. I nostri Leandro e Fabrizio si sono cimentati con risultati abbastanza generali (molto bravi!), ma preferiamo non andare troppo a fondo della questione che ha anche visto discussioni (ancora aperte) tra gli specialisti. Inseriamo, comunque, un link a un metodo semi-grafico che può interessare i più accaniti matematici.

Il problema che volevamo affrontare era relativamente semplice: trovare un segmento che dividesse il triangolo di partenza in due parti che avessero sia la stessa area che lo stesso perimetro.

Nella Figura 1, chiamiamo a, b e c i tre lati del triangolo e x e y i segmenti AP e AQ, tali da definire il segmento PQ capace di affettare il triangolo secondo quanto richiesto dal quiz. Chiamiamo α l’angolo in A. Ovviamente sia x che y devono essere maggiori o uguali a zero, dato che P e Q devono cadere lungo i lati AB e AC. Analogamente, essi non possono superare i valori a e b, altrimenti cadrebbero al di fuori del triangolo.

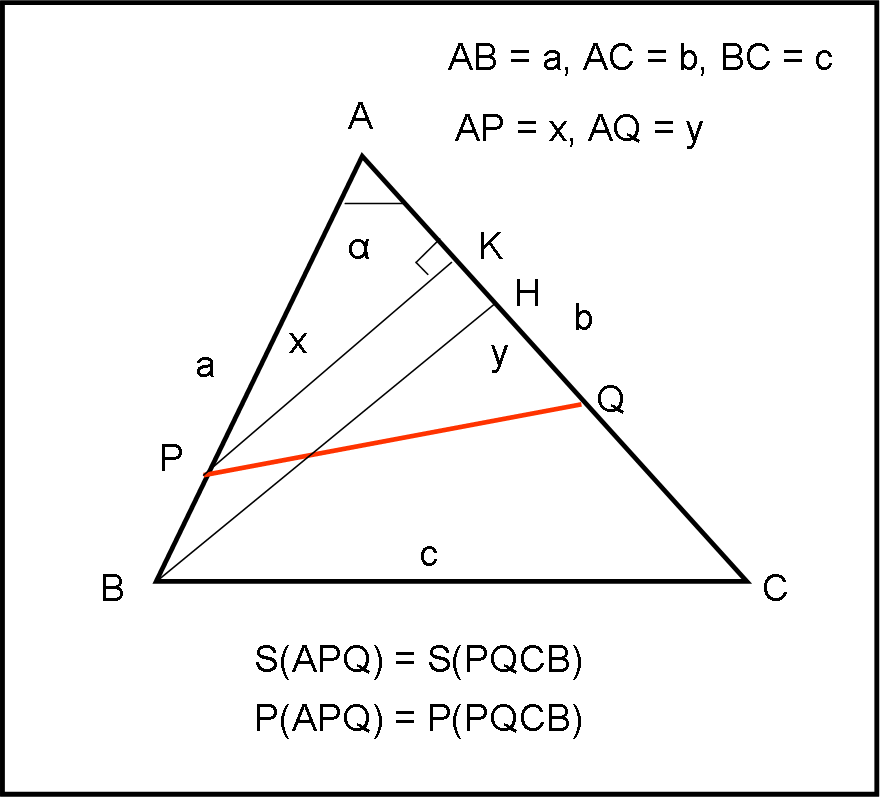
Cominciamo a scrivere la relazione che ci obbliga ad avere APQ = PQBC, ossia l’uguaglianza dei due perimetri.

La relazione può essere scritta:

AP + PQ + QA = PQ + QC + BC + PB

Ricordando che AP = x e AQ = y e che AB = a, AC = b e BC = c, si ha:

x + PQ + y = PQ + (b – y) +(a – x) + c

Semplificando:

x + y = b – y + a – x + c

2x + 2y = a + b + c

x + y = (a + b + c)/2

La prima relazione ci dice che la somma di x e y deve essere uguale al semiperimetro del triangolo.

Passiamo adesso alle aree. Prima di tutto notiamo che dire che il segmento PQ divide l’area del triangolo ABC in due parti uguali, vuole anche dire che una delle due aree trovate deve essere la metà dell’area del triangolo originario. In altre parole:

S(APQ) = ½ S(ABC)

Ricordiamo che l’area di un triangolo è dato da base per altezza diviso due. Consideriamo come base AC. La sua altezza è BH. Ma:

BH = AB sen(α)

Ne segue che:

S(ABC) = ½ AC AB sen(α)

Consideriamo, adesso, l’area del triangolo APQ. Come base prendiamo AQ = y e come altezza PK. Tuttavia, si ha che:

PK = AP sen(α)

L’area di APQ diventa perciò:

S(APQ) = ½ AQ AP sen(α)

In conclusione la relazione da rispettare deve essere:

½ AQ AP sen(α) = ½ (½ AC AB sen(α))

Semplificando e sostituendo:

x y = ½ ab

In conclusione, le due relazioni per “affettare” nel modo richiesto il triangolo di partenza sono

x + y = (a + b + c)/2 = somma delle soluzioni = S

x y = ½ ab  = prodotto delle soluzioni = P                             .... (1)

Una regola, facilmente dimostrabile (provateci da soli… e magari, poi, la descriveremo), delle equazioni di secondo grado ci dice che conoscendo la somma S e il prodotto P delle due soluzioni, l’equazione risolvente si scrive (utilizzando una variabile qualsiasi t):

t² – S t + P = 0

di cui x e y sono le soluzioni.

Nel nostro caso, si ha:

S = (a + b + c)/2

P = ½ ab

L’equazione risolvente diventa quindi:

t² – (a + b + c)t/2 + ½ ab = 0

Risolvendola si hanno i valori di x e y:

t = (x,y) = ((a + b + c)/2 +/- ((a + b + c)²/4 – 2ab)^1/2)/2

Ossia:

x = ½((a + b + c)/2 + ((a + b + c)²/4 – 2ab)^1/2

y = ½((a + b + c)/2 - ((a + b + c)²/4 – 2ab)^1/2

e viceversa (ossia una coppia di x e y con i valori invertiti)

Se questo procedimento vi sembra complicato, basta tornare alle (1) e considerare le due equazioni come facenti parti di un sistema in due equazioni in due incognite.

Da una equazione si ricava x (o y). Si inserisce nell’altra e si ottiene un’equazione di secondo grado in y (o x). Risolvendola si trovano nuovamente le soluzioni precedenti. In un modo o nell’altro si ottengono due coppie di x e y che portano a due soluzioni “teoriche” per il segmento PQ.

Quanto fatto per i lati a e b può essere ripetuto per la coppia a e c e per quella b e c.

Sembrerebbe, a prima vista, che ci siano sempre due soluzioni per il segmento PQ. E la stessa cosa dovrebbe succedere per quelli analoghi ottenibili con le altre due coppie di lati. In totale dovrebbero perciò esistere, teoricamente, sei possibili segmenti che affettano il triangolo come richiesto dal quiz.

In realtà, ciò non è vero, perché molto dipende dal segno di ciò che sta sotto radice. Ossia, per avere soluzioni REALI, ciò che sta sotto radice deve essere maggiore o uguale a zero, altrimenti avremmo la radice quadrata di un numero negativo. Deve perciò essere:

(a + b + c)²/4 – 2ab ≥ 0

Ma non basta ancora…

Sia x che y devono essere maggiori di zero e minori di a e/o b (e cosa analoga per le altre coppie di lati). Questo fatto vincola ancora di più la plausibilità dei risultati ottenuti per x e y.

Si può dimostrare in vari modi, tutti piuttosto elaborati, che le soluzioni non possono mai essere più di tre, ma che comunque ce ne deve essere, sempre, almeno una. Molto dipende dal tipo di triangolo che si utilizza: isoscele, equilatero, rettangolo o scaleno.

Divertitevi pure a considerare alcuni triangoli più o meno particolari e trovare le soluzioni reali.

Per coloro che vogliono arrivare fino in fondo, posso consigliare questo metodo semi-grafico. Buon divertimento sia a loro che a chi si limiterà a qualche prova pratica…

Il QUIZ lo trovate QUI.