Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Continuiamo, seguendo Keplero, verso la sua equazione fondamentale  che lega anomalia eccentrica e anomalia media. Un'equazione fondamentale che può, però, risolversi solo per approssimazioni successive, un processo, oggi, ridicolo per i calcolatori elettronici. Pensiamo, però, a Keplero che non li aveva ancora...

La volta scorsa (QUI) abbiamo introdotto facilmente il moto medio n. Richiamiamolo velocemente:

n = 2π/P       …. (13)

che non è altro che la velocità angolare media del pianeta, come se fosse inserito in un’orbita circolare.  In realtà, a volte, il pianeta la supera e a volte è più lento, ma al completamento dell’orbita tutto torna al suo posto. Una grandezza facilissima da calcolare e che si ricava dall’area RPS della Fig. 5. che riproponiamo per semplicità.

Si ha subito che n(t – t₀) è l’angolo descritto nell’intervallo di tempo  (t – t₀) da un raggio vettore che ruoti attorno a S con velocità angolare costante n. E’ immediato introdurre una nuova anomalia, detta anomalia media M data da:

M = n(t – t₀)       …. (14)

Da cui, utilizzando la (13) e la (14):

area RPS = πab(t – t₀)/P = 2πab(t – t₀)/2P = n a b (t - t₀)/2 = ½ a b M       …. (15)

Cerchiamo adesso di scrivere quest’area come somma dell’area SRU e dell’area URP, in modo da far comparire l’anomalia eccentrica E).

area RPS = area SRU + area URP       …. (15 a)

Nessun problema per la prima:

area SRU = ½ SU ∙ RU

 

Tuttavia, sappiamo anche che CS = ae  (QUI - fig. 1)

SU = CU – CS = a cosE – ae

Ricordando la (2. QUI):

RU = r sen f = b sen E

Si ha, in definitiva:

area SRU = ½ (a cos E – ae)(b sen E) = ½ (ab cos E sen E - e ab sen E)

area SRU = ½ ab sen E (cos E – e)      …. (16)

Un po’ più complicato è il calcolo dell’area URP. Per seguire meglio l’operazione usiamo la Fig. 8.

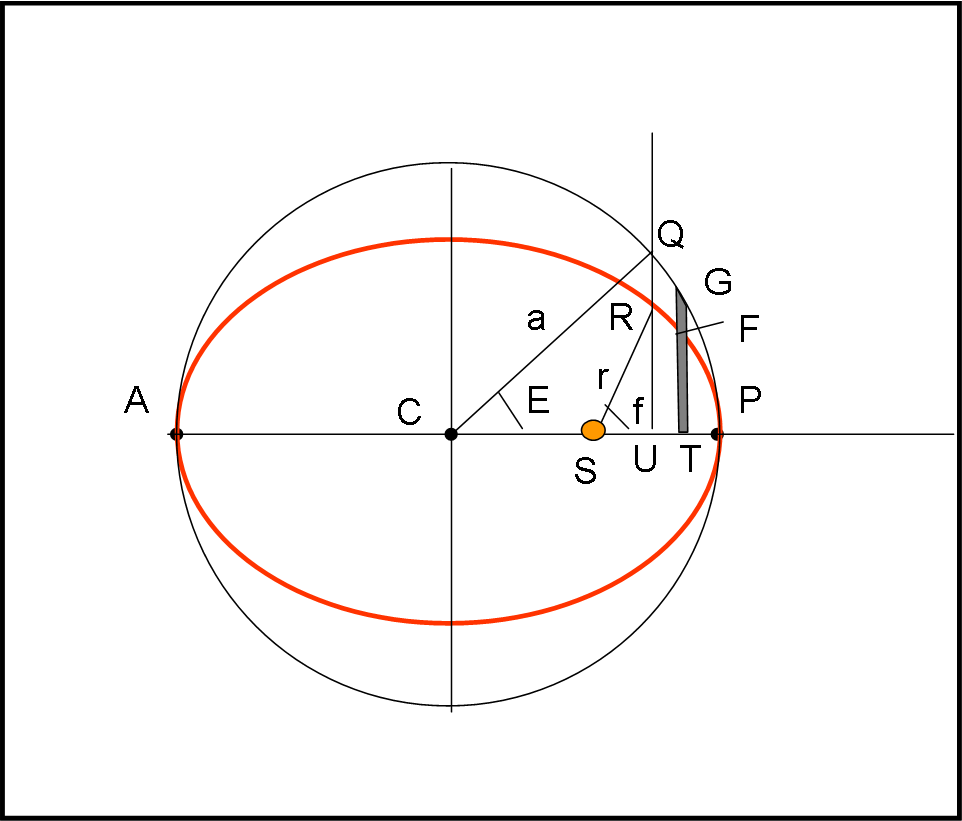
Tracciamo delle strisce di base infinitesima, perpendicolari a PC, che arrivino fino alla circonferenza di raggio CP = a.

Da quanto imparato precedentemente (QUI – formula 1), sappiamo che:

QU/RU = a/b

Dato che la base ha una dimensione infinitesima, si ha:

area striscia FT/area striscia GT = b/a

Ne segue che la somma di tutte le strisce  che formano l’area URP (le strisce del tipo FT) deve essere b/a volte la somma di tutte le strisce che formano l’area UQP (le strisce del tipo GT).

In altre parole:

area URP = b/a area UQP

Tuttavia l’area UQP non è altro che l’area del settore circolare CQP meno l’area del triangolo QCU. In parole matematiche:

area URP = b/a area UQP = b/a (area CQP – area QCU)        …. (17)

Tutti dovremmo sapere quanto vale l’area di un  settore circolare… comunque si può ricavare immediatamente attraverso la proporzione:

Area cerchio: 360 = Area settore: angolo al centro del settore.

Nel nostro caso si ha:

πa²/2π = area CQP/E

Ossia:

area CQP = a²E/2

L’area  del triangolo QCU è, ovviamente:

area QCU = ½ QU ∙ CU = ½ a sen E ∙ a cos E = ½ a² sen E cos E

Possiamo tranquillamente scrivere la (17):

area URP = b/a (a² E/2 - a² sen E cos E/2)

area URP = ½ ab (E – sen E cos E)     …. (18)

Non ci resta, adesso, che prendere la (16) e sommarla alla (18) per ottenere l’area di  RPS, come dice la (15a):

area RPS = area SRU + area URP = ½ ab sen E (cos E – e) + ½ ab (E – sen E cos E)

area RPS = ½ ab (sen E cos E – e sen E + E – sen E cos E)

area RPS = ½ ab (E – e sen E)       …. (19)

Ancora un piccolo sforzo, uguagliando la (15) con la (19):

½ ab M = ½ ab (E – e sen E)

M = E – e sen E      …. (20)

La (20) è il risultato di un ragionamento geniale ed è di eccezionale importanza. Essa viene chiamata Equazione di Keplero e permette di legare l’anomalia eccentrica con quella media. Vi invito caldamente di seguire i vari calcoli eseguiti, con molta calma e attenzione. Vi renderete conto della bellezza e armonia del metodo. Un piccolo grande capolavoro geometrico-matematico.

Già sapevamo come ricavare l’anomalia vera dall’anomalia eccentrica e quindi il problema sembrerebbe praticamente risolto: conoscendo l’eccentricità e e l’anomalia media M si può ricavare, attraverso l’anomalia eccentrica E, l’anomalia vera f.  Una vera poesia, un’opera d’arte scientifica…

Tutto risolto? Nemmeno per sogno! Provate a risolvere la (20) per ricavare la E  e vi troverete in grande difficoltà (sia sen E che E sono espressi in radianti). Purtroppo l’equazione di Keplero è un’equazione trascendente e non si può risolvere in modo diretto…

Poco male sia per Keplero che, soprattutto, per le possibilità di calcolo odierne. Basta risolverla  per approssimazioni successive… cosa che vedremo la prossima volta.

QUI trovate tutti gli articoli su “Gli elementi orbitali e i loro compari”

Chi ha voglia e curiosità di fare due chiacchiere con Keplero in persona (e non solo lui), può trovarlo QUI