Questo articolo è stato inserito nella pagina di approfondimento dedicata alla Meccanica Celeste.

 

In questo articolo, torniamo alle leggi di Keplero per definire ancora meglio le loro enormi potenzialità, specialmente se legate alla legge di Newton. Vi assicuro che sono argomenti tutt’altro che noiosi e -forse- non troppo conosciuti.

Innanzitutto, parliamo di qualcosa che tutti dovrebbero conoscere: gli elementi orbitali. Tuttavia, vedremo che la determinazione degli elementi orbitali non permette di ricavare immediatamente la posizione di un pianeta nella sua orbita. La faccenda è piuttosto complicata e ha dato non pochi grattacapi allo stesso Keplero, che l’ha però affrontata e risolta con una sapienza a dir poco inaspettata per i suoi tempi.

L’orbita di un pianeta, di un satellite naturale o di un satellite artificiale può essere definita in vari modi. Noi consideriamo quello classico, usato normalmente per i pianeti e i corpi minori del Sistema Solare. Alcune misure angolari cambiano quando si parla dei satelliti dei pianeti e delle comete. I parametri che definiscono un’orbita vengono chiamati elementi orbitali.

Innanzitutto, va tenuto presente che nessun corpo planetario ha degli elementi orbitali fissi, dato che essi variano continuamente per effetto delle perturbazioni dei compagni di viaggio. In questo articolo ci riferiamo, quindi, ai parametri orbitali nel caso kepleriano, ossia nel problema dei due corpi. In altre parole, quelli relativi a un orbita ricavata dalla legge di gravitazione universale di Newton. Inoltre, essi si riferiscono a un sistema non-inerziale, ossia a un sistema relativo a uno dei due corpi, specificatamente il Sole (o il pianeta per i satelliti). In altre parole, essi vengono definiti considerando come fissa la posizione della massa principale (Sole o pianeta) e analizzando la traiettoria del secondo corpo intorno al primo. Sappiamo, infatti benissimo, che due corpi rivolvono, in realtà, attorno al baricentro del sistema.

Gli elementi orbitali necessari a definire un’orbita e, di conseguenza, a calcolare la posizione del corpo celeste in ogni momento (effemeridi) sono sei. Essi possono essere divisi in tre gruppi (o meglio quattro).

Il primo gruppo (due parametri) serve a definire la forma dell’orbita come si presenta sul proprio piano orbitale. Il secondo (due parametri) serve a definire l’orientamento del piano orbitale rispetto a un piano di riferimento (l’eclittica per i pianeti e il piano equatoriale per i satelliti). Il terzo gruppo (un parametro) definisce l’orientamento dell’orbita nel suo piano. Il quarto gruppo (un parametro) è molto particolare ed è quello che definisce la posizione dell’oggetto lungo la sua orbita. Si può facilmente notare che esso è il solo ad avere bisogno del tempo. Tutti gli altri definiscono soltanto la traiettoria, in cui il pianeta può anche non esistere, l’ultimo lo inserisce nella posizione che occupa realmente a un certo istante.

Dato che, come già detto, gli elementi orbitali variano col tempo, è necessario aggiungere un ulteriore parametro che indichi a quale data si riferiscono i parametri orbitali. Esso serve, in pratica, a stabilire con esattezza il sistema di riferimento usato. Alcuni lo considerano un “settimo” elemento, ma in realtà non ha niente a che fare con la descrizione kepleriana.

Iniziamo a definirli esattamente, utilizzando varie figure.

Il primo gruppo (Fig. 1) contiene i due parametri più conosciuti: semiasse maggiore a ed eccentricità e (vedi QUI). Il primo ci dice qualcosa sulla distanza media dal Sole (posto in un fuoco dell'ellisse) e il secondo quanto l’orbita sia allungata. Da essi si deducono subito due distanze estremamente particolari e molto usate: la distanza perielica q e la distanza afelica Q. La prima identifica il punto di minima distanza raggiungibile dal pianeta rispetto al Sole (perielio P) e la seconda il punto di massima (afelio A).

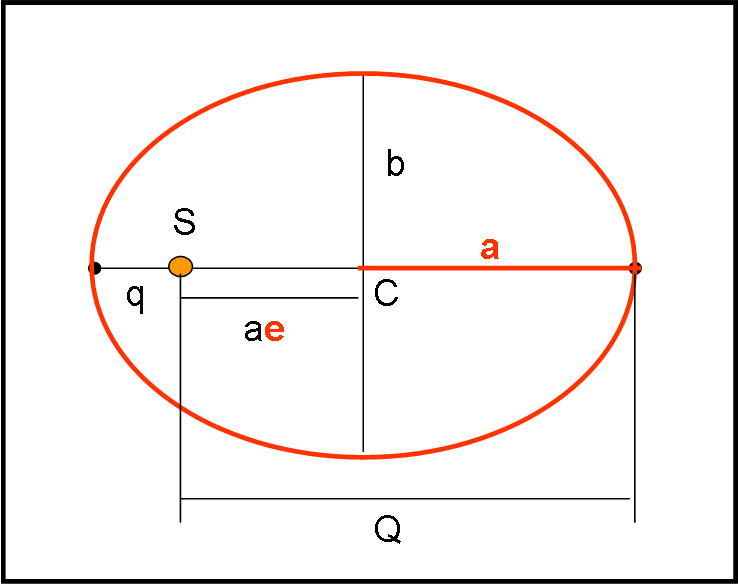
Le formule che permettono di ricavare queste due grandezze “ausiliarie” sono:

q = a(1 - e)

Q = a(1 + e)

Ovviamente, nel caso in cui e = 0, cadiamo nel caso di un’orbita circolare, con il Sole che si porta nel centro C e il semiasse che diventa il raggio della circonferenza. Perielio e afelio perdono di significato.

Il secondo gruppo (Fig. 2) è formato, innanzitutto, dall’inclinazione i del piano dell’orbita rispetto al piano dell’eclittica. Esso serve, immediatamente, a definire la linea dei nodi, ossia la linea intersezione tra i due piani (ne abbiamo parlato anche QUI). Nel suo moto di rivoluzione attorno al Sole, il pianeta passa da una parte all’altra della sfera celeste, centrata nel Sole,  rispetto al piano dell’eclittica. Il nodo ascendente N è quello che vede il passaggio del pianeta diretto verso l’alto. In N’ (nodo discendente) avviene il contrario: il pianeta scende verso il basso.

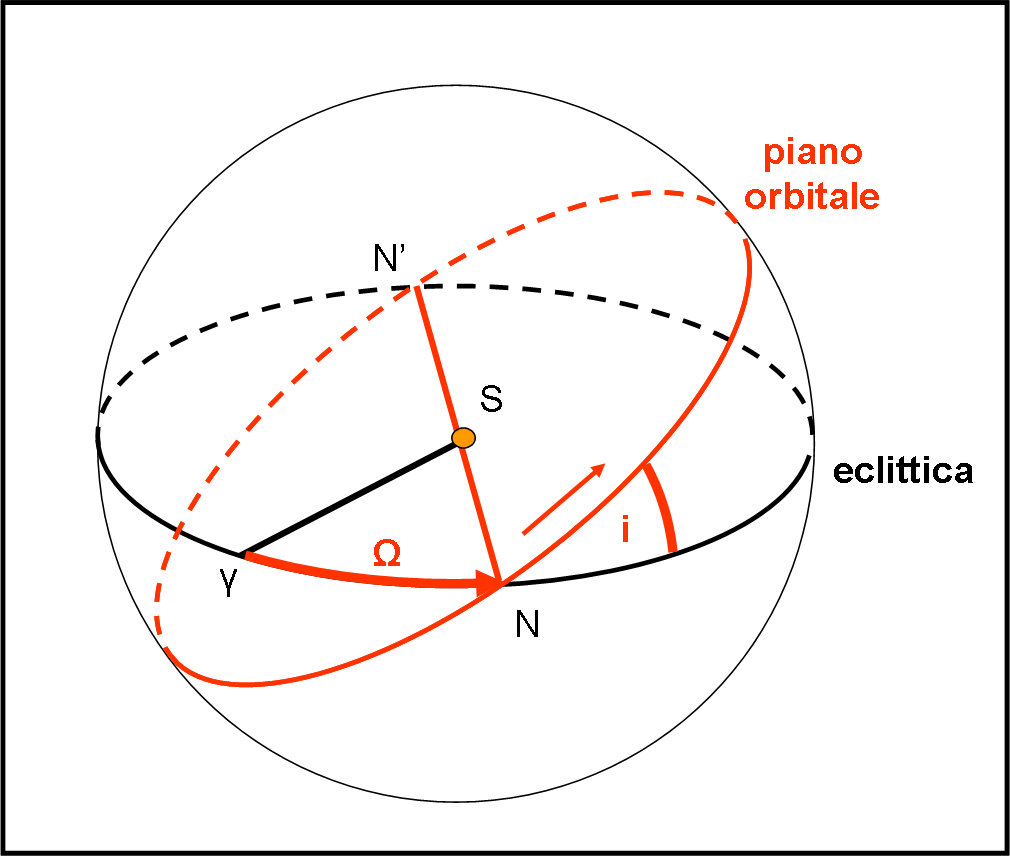
Definita una linea fissa sul piano dell’eclittica (si sceglie  la direzione del punto γ di cui parleremo a lungo nella trattazione dei sistemi di riferimento e che rappresenta la linea dei nodi tra piano dell'equatore terrestre ed eclittica) si definisce come longitudine del nodo ascendente  Ω l’arco di cerchio massimo γN (o -se preferite- l’angolo in S tra γ e N). Dell’arco di cerchio massimo abbiamo parlato nella lezione 3 della geometria sferica.

Con questi due parametri abbiamo piazzato in modo univoco il piano orbitale rispetto al piano di riferimento che è l’eclittica.

La forma dell’orbita è stata stabilita così come la posizione del piano orbitale rispetto all’eclittica. Non ci resta, adesso, che trovare la posizione dell’orbita sul suo piano orbitale. In poche parole, prendiamo una linea particolare dell’orbita e fissiamola rispetto a un'altra linea ben determinata della sua orbita. Queste due linee sono la linea degli apsidi, ossia la congiungente afelio-Sole-perielio (ossia quella che misura l’asse maggiore dell’ellisse) e la linea dei nodi determinata precedentemente. Siamo di nuovo in un problema piano.

Il terzo gruppo (Fig. 3) è composto dall’angolo formato dalla direzione Sole-nodo ascendente e la direzione Sole-perielio, che viene chiamato argomento del perielio ω. A questo punto è come se avessimo incollato l’orbita (che ha una forma ben determinata) sul suo piano orbitale che a sua volta è stato bloccato univocamente rispetto all’eclittica.

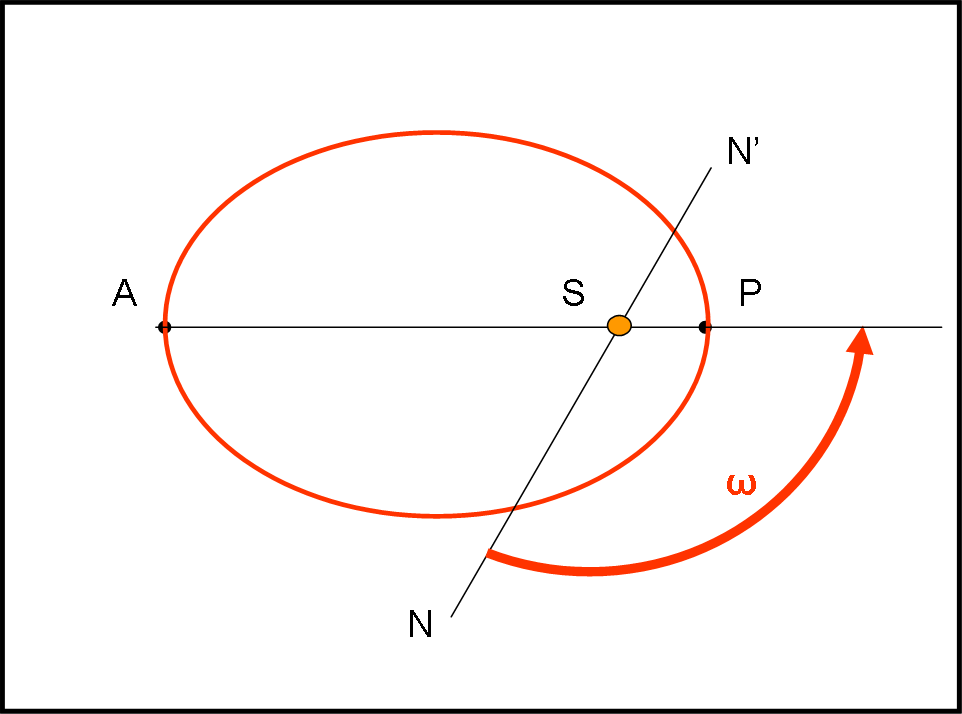
La parte puramente geometrica si è conclusa e la riassumiamo nella Fig. 4.

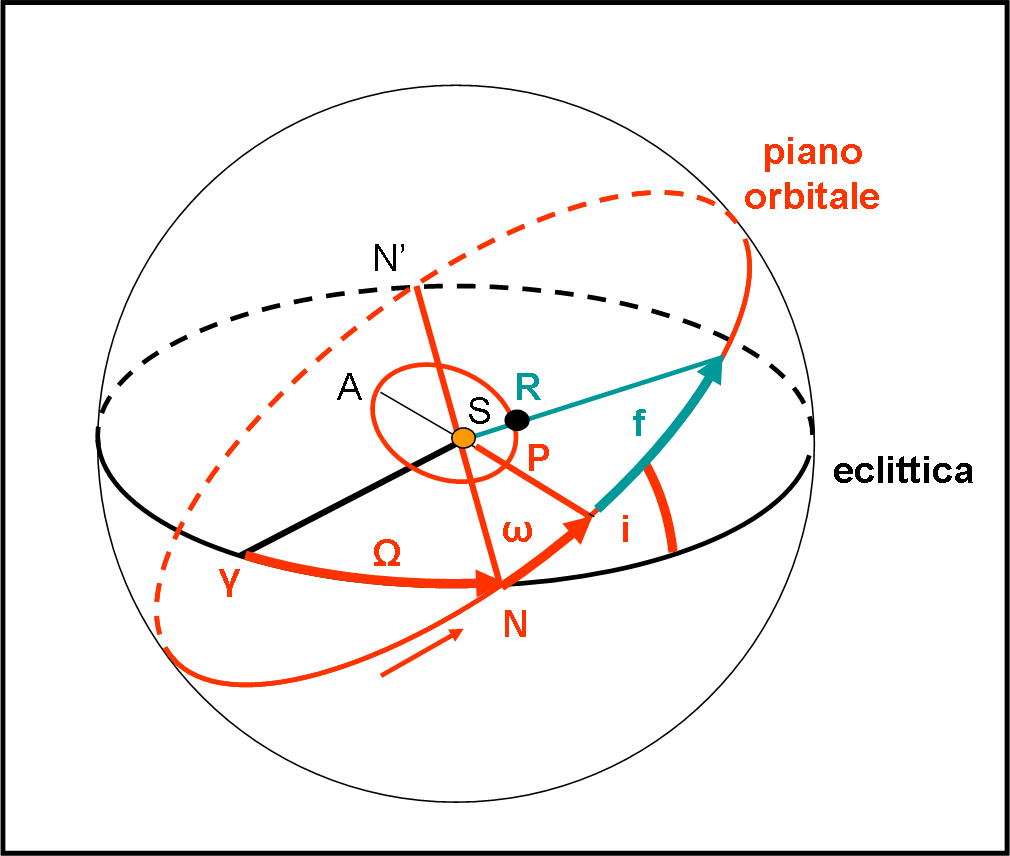
A questo punto non resta che inserire il vero pianeta nella sua orbita e vedere dove si trova.

Un modo per determinare questa situazione è quella di indicare il tempo in cui il pianeta passa al perielio e poi determinare la posizione attuale rispetto al perielio. Ciò comporta la conoscenza dell’angolo al Sole tra perielio e pianeta, ossia la conoscenza dell’angolo chiamato anomalia vera f.

In teoria, esso deriva direttamente dalla seconda legge di Keplero (la velocità areolare è costante), ma il suo calcolo effettivo è tutt’altro che semplice, da un punto di vista matematico. Esso, infatti, è un angolo che varia continuamente col tempo in modo non lineare (il pianeta cambia continuamente la sua velocità). E’ molto più conveniente usare un angolo “ausiliario” che vari linearmente col tempo e che sia legato all’anomalia vera. Un bel problemino che introduce un altro angolo ausiliario, ma che semplifica di molto il calcolo della posizione finale del pianeta.

Ne consegue che, invece di indicare il tempo di passaggio al perielio, si indica l’anomalia media M a una certa data e, attraverso di lei (che varia linearmente), si determina l’anomalia vera e la posizione reale del pianeta.

L’anomalia media è un angolo che non corrisponde a un effettivo angolo geometrico visibile in figura, per cui si preferisce sempre indicare l’anomalia vera (l’angolo VERO, appunto).

Il problema di passare dall’anomalia media, di facile calcolo, all’anomalia vera prende anche il nome di problema di Keplero, che lui riuscì a risolvere in modo geniale anche se abbastanza approssimato. Oggi, con i computer, la trasformazione è di irrisoria facilità.

Quanto detto spiega perché in molti testi si continui a dare come sesto elemento orbitale il tempo di passaggio al perielio, mentre invece si trova indicata l’anomalia media nei testi professionali che servono effettivamente a ricavare la posizione del pianeta a ogni istante.

Certi angoli vengono chiamati anomalie fin dall’antichità, dato che rappresentavano “anomalie” rispetto a un moto perfettamente circolare.

In realtà (come già accennato), la conoscenza degli elementi orbitali non permette una posizione del pianeta abbastanza accurata, dato che le perturbazioni degli altri pianeti li modificano continuamente e vari effetti a lungo periodo, come la precessione degli equinozi, sposta in maniera sensibile la direzione del punto γ. E’ per questo che gli elementi orbitali sono sempre accompagnati da un’epoca di riferimento attraverso la quale può essere calcolata facilmente la posizione di γ all’epoca attuale. In generale, comunque, la determinazione della posizione di un pianeta abbisogna della soluzione (più o meno accurata) del problema degli n corpi (risolvibile solo attraverso integrazioni numeriche).

Per determinare un’orbita approssimata o -meglio- kepleriana sono necessari sei parametri. Ciò vuol dire, matematicamente parlando, che abbiamo sei incognite. E’ necessario, perciò, determinare almeno sei equazioni in cui compaiano le sei incognite (in realtà, molte di più in modo da applicare il metodo dei minimi quadrati). Nei metodi “classici” bastavano tre posizioni e tre velocità, osservate da terra, per ottenere gli elementi orbitali. Oggi si usano metodi anche molto diversi. Tuttavia, il problema della determinazione degli elementi orbitali è, ormai, un lavoro di routine, effettuato, quasi automaticamente, in alcuni centri specializzati. Il volerli calcolare “in casa” è solo e soltanto un simpatico esercizio di ben poca utilità pratica. Analogo discorso vale per il problema opposto: passare dagli elementi orbitali alla posizione reale all’istante desiderato (calcolo delle effemeridi).

E’, invece, oltremodo interessante (non solo storicamente) descrivere meglio il legame tra anomalia media e anomalia vera, ossia andare a fondo del problema di Keplero. Sotto questo punto di vista, è più che giusto dare grande risalto all’anomalia eccentrica e all’equazione di Keplero, un piccolo grande capolavoro di meccanica, risolto prima ancora che questa disciplina nascesse realmente…

Ne consegue che, tanto per richiamare una nuova voce di Wikipedia, aggiunta da un nostro lettore, ha poco senso parlare singolarmente delle varie anomalie, ma è fondamentale trattarle tutte  assieme, per potere veramente comprendere il loro significato teorico e “pratico”. Ed è quello che andiamo a fare, scoprendo che l’interesse non è certo trascurabile…

Capisco benissimo che l’argomento possa sembrare uno di quei noiosi e inutili procedimenti geometrici e matematici. Tuttavia, vi invito a non pensarla così e a dedicargli un poco del vostro tempo. Il pensare che Keplero sia stato in parte fortunato e in parte “brutalmente” empirico nella determinazione delle sue leggi è assolutamente falso. A parte l’aver saputo sfruttare al meglio le fantastiche osservazioni di Tycho Brahe, è indubbio che solo un uomo di eccezionale intuizione e di grande capacità di sintesi poteva arrivare al risultato ottenuto. La strada a Newton non poteva essere preparata meglio.

La sua grandezza è ulteriormente confermata da quello che viene riportato in questo articolo. La relazione tra l’angolo teoricamente fondamentale (anomalia vera) e gli angoli quasi astratti utilizzati da Keplero è un capolavoro di genialità e, quindi, di semplicità. Se pensiamo che è stato realizzato ben prima che nascesse la meccanica celeste, esso acquista un valore enorme sia dal punto di vista storico che pratico. Ancora oggi si utilizza comunemente, anche se sveltito in modo impressionante dai calcolatori elettronici.

Gustiamolo per quello che è e diamo a Keplero un valore che supera sicuramente l’apparente empirismo delle tre leggi. In conclusione: non perdetelo e seguitelo attentamente, sarà un vero regalo per delle menti che desiderano apprendere e capire l’armonia e l’eleganza della matematica e della meccanica, il linguaggio essenziale per vivere nel Cosmo con umiltà e orgoglio.

Anomalia eccentrica

All'inizio abbiamo definito gli elementi orbitali, ponendo particolare attenzione sul tempo di passaggio al perielio e, di conseguenza, sul calcolo dell’anomalia vera f, ossia sulla determinazione della posizione del corpo planetario lungo la sua orbita. Abbiamo visto che la seconda legge di Keplero potrebbe risolvere la questione, ma che, in realtà, il calcolo sarebbe oltremodo complesso e si preferisce introdurre al posto di f degli angoli ausiliari. Questo procedimento prende proprio il nome di problema di Keplero.

Cominciamo con lo scrivere la seconda legge di Keplero, ricordando ciò che dice: le aree descritte dal raggio vettore (congiungente Sole-pianeta) sono proporzionali ai tempi impiegati a descriverle. Facciamo riferimento alla Fig. 5.

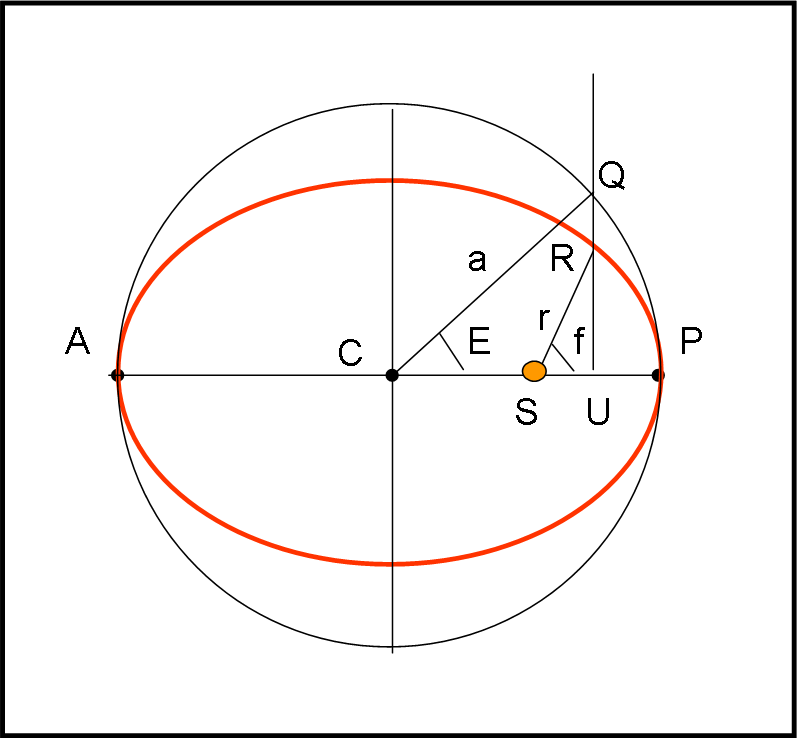
Ciò vuole anche dire che l’area dell’intera ellisse sta all’area descritta da SR come il periodo orbitale P sta al tempo trascorso dal passaggio al perielio al tempo relativo alla posizione R. In parole più sintetiche:

Area (SRP)/πab = (t – t₀)/P              ( a e b semiassi dell’ellisse)

Area (SRP) = πab(t – t₀)/P

Come già detto, il secondo membro è noto e dall’area si potrebbe dedurre la posizione di R. Ma, il calcolo è complesso e Keplero si mise all’opera…

Introduciamo la grandezza moto medio n, dato da:

n = 2π/P

che non è altro che la velocità angolare media del pianeta, come se fosse inserito in un’orbita circolare.  In realtà, a volte il pianeta la supera e a volte è più lento, ma al completamento dell’orbita tutto torna al suo posto. Una grandezza facilissima da calcolare, che ci servirà in seguito.

Tracciamo in figura il cerchio di raggio a e di centro C. Notiamo che se il pianeta descrivesse la circonferenza e se il Sole fosse al centro la sua velocità, costante, sarebbe proprio il moto medio.

Noi, invece, tracciamo da R la perpendicolare a CP e l’allunghiamo fino a incontrare la circonferenza in Q. Introduciamo l’angolo E (QCP) e lo chiamiamo anomalia eccentrica.

E è un angolo davvero “simpatico” (ma non solo…). Confrontiamolo con l’anomalia vera f in Fig. 6.

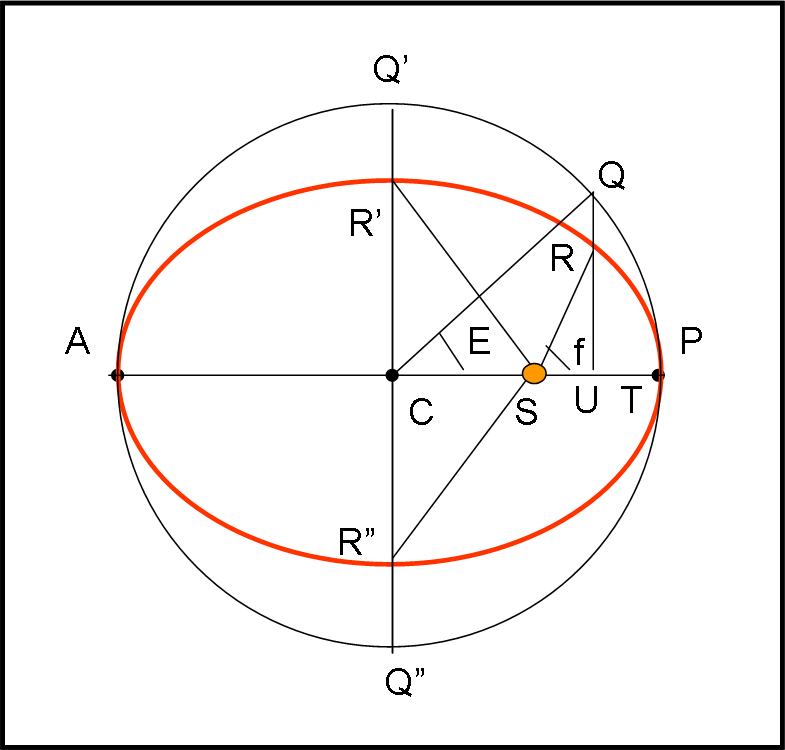
Quando il pianeta è al perielio P, i punti R e Q coincidono ed è E = f = 0.  Quando il punto R si porta in R’, Q arriva in Q’. Sono entrambi sulla verticale passante per C e l’angolo E è uguale a 90°, decisamente più piccolo di f. Tuttavia, essi tornano a essere uguali quando il pianeta raggiunge l’afelio A. Sembra quasi che E abbia accelerato per raggiungere f. Quando R si porta in R”, Q” sta anch’esso sulla verticale tracciata da C, una situazione simile a quella relativa a E = 90°. Ma, adesso E = 270°, mentre f è decisamente più piccolo. E’ lui che adesso deve accelerare per raggiungere, nuovamente, E al perielio P. Una corsa davvero interessante che fa sicuramente pensare che E ed f siano legati assieme da una qualche relazione. D’accordo che E non è un angolo misurabile, ma è già qualcosa. Oltretutto, non ci può scappare una certa analogia con l’anomalia media…

La faccenda si fa interessante. Dedichiamoci al legame tra anomalia vera e anomalia eccentrica. C’è da divertirsi…

Innanzitutto c’è da ricordarsi o da ricavare un’altra proprietà dell’ellisse che a noi va proprio a fagiolo:

QU/RU = a/b           …. (1)

L’ellisse è veramente una figura fantastica… Come si ottiene questa relazione? Qui di seguito riportiamo la dimostrazione e la scriviamo in corsivo. Chi non la conosce la può leggere, gli altri possono saltarla.

Usiamo la Fig. 7, dove abbiamo disegnato due cerchi concentrici di raggio a e b, rispettivamente.

Tracciamo una qualsiasi retta CQ. Il punto B (intersezione di questa retta con la circonferenza più piccola) appartiene alla circonferenza di raggio b e la sua ordinata y = BD è data da:

y_b = BD = b sen E

Il punto Q appartiene, invece, alla circonferenza di raggio a e la sua ascissa CU è data da:

 x_a = CU = a cos E

Bene, senza fare tanti passaggi possiamo dimostrare facilmente che il punto R dell’ellisse ha coordinate

x = a cos E

y = b sen E

Proviamo? Basta elevare a quadrato le due relazioni:

x²/a² = cos²E

y²/b² = sen²E

Sommiamole e si ottiene:

x²/a² + y²/b² = cos²E + sen²E = 1

Ma un’equazione del tipo:

x²/a² + y²/b² = 1

è proprio l’equazione di un ellisse di semiassi a e b.

Il che vuole dire che RU è uguale a BD, dato che entrambi valgono b sen E. Possiamo, allora considerare i triangoli rettangoli CUQ e CDB.

Essi sono, ovviamente, simili e quindi vale la relazione:

QC/BC = QU/BD

Ma… RU è uguale a BD e quindi segue che:

a/b = QU/RU

Proprio quello che volevamo dimostrare.

Torniamo alla Fig. 5, che ci permette di scrivere:

RU = r sen f                                 (r è il raggio vettore)

QU = a sen E

Utilizzando la (1), si ottiene:

a/b = QU/RU = a sen E/r sen f

ossia:

r sen f = b sen E                   …. (2)

Dedichiamoci a SU che vale:

SU = r cos f

Tuttavia SU è anche :

SU = CU – CS

Come sappiamo bene dallo studio dell’ellisse (QUI, capitolo 15)

CS = ae                  (distanza tra centro e fuoco)

CU è invece dato da:

CU = a cos E

Ne segue che:

SU = r cos f  =  a cos E – ae = a(cos E – e)

r cos f  = a(cos E – e)              …. (3)

Eleviamo a quadrato la (2) e la (3) e sommiamole:

r² sen ²f  + r² cos² f  = b² sen²E + a²(cos E – e)²

r² = b² sen²E + a²(cos E – e)²

Sappiamo, però, che (QUI, capitolo 15):

b² = a²(1 – e²)

Sostituendo, si ha:

r² = a²(1 – e²) sen²E + a²(cos E – e)²

Eseguiamo il quadrato di un binomio (QUI, capitolo PN, l'ultimo)

r² = a²sen²E – a²e²sen²E + a²cos²E + a²e² – 2a²e cosE

r² = a²sen²E + a²cos²E + a²e² – a²e²sen²E – 2a²e cosE

Ricordiamo che sen²E + cos²E = 1 e che, analogamente, 1 – sen²E = cos²E

r² = a² + a²e²cos²E – 2a²e cosE

Raccogliendo a², al secondo membro compare il quadrato di un binomio

r² = a²(1 + e²cos²E – 2e cosE) = a²(1 – e cosE)²

E, infine, estraendo la radice quadrata:

r = a(1 – e cosE)        …. (4)

A questo punto dobbiamo introdurre le formule di bisezione (la trigonometria è ricchissima di formule…). Non ve le voglio assolutamente dare dall’alto, ma ricaviamole semplicemente da ciò che già sappiamo. In particolare nel quiz sul barattolo e la formica (QUI), abbiamo introdotto le formule di addizione e sottrazione (la loro dimostrazione è data nell’appendice di quell’articolo). A noi interessa la seconda, ossia:

cos(α + β) = cos α cos β - sen α sen β

La utilizziamo nel caso particolare in cui α = β. Si ottiene:

cos(2α) = cos²α - sen²α          …. (5)

Con questa formuletta si può giocare in due modi molto simpatici:

a) Scriviamo, come ormai sappiamo molto bene:

cos²α = 1 - sen²α

La (5) diventa:

cos(2α) = 1 - sen²α - sen²α = 1 - 2 sen²α

Poniamo adesso, tanto per restare vicini al nostro problema (che è poi quello di Keplero):

2α = f

Si ha:

cos f = 1 - 2 sen²(f/2)

Da cui:

2 sen²(f/2) = 1 – cos f             …. (6)

b) Scriviamo, come sappiamo altrettanto bene:

sen²α = 1 - cos²α

Inseriamola nella (5):

cos(2α) = cos²α – (1 - cos²α) = 2 cos²α – 1

Come prima, poniamo 2α = f e otteniamo:

cos f = 2 cos²(f/2) – 1

Da cui:

2 cos²(f/2) = 1 + cos f              …. (7)

Notiamo quante cose si possono fare partendo dalla semplice relazione fondamentale sin²(α) + cos²(α) = 1. Sembra quasi impossibile… la matematica sa essere fantasiosa e sorprendente come poche altre discipline!

Torniamo a noi con la (6) e la (7). Tanto per gradire moltiplichiamole per r:

2 r sen²(f/2) = r(1 – cos f)

2 r cos²(f/2) = r(1 + cos f)          …. (8)

Dobbiamo cercare di scrivere i secondi membri in funzione dell’anomalia eccentrica E. Andiamo a cercare, nella trattazione precedente, qualche relazione utile allo scopo.

Una è la (3), che dice:

r cos f  = a(cos E – e)

Un’altra è la (4) che dice:

r = a(1 – e cosE)

Riscriviamo le (8) e andiamo a sostituire ciò che dicono la (3) e la (4)

2 r sen²(f/2) = r(1 – cos f) = r – r cos f = a(1 – e cosE) - a(cos E – e)

2 r sen²(f/2) = a - ae cos E – a cosE + ae = a(1 + e) – a cosE (1 + e)

2 r sen²(f/2) = a(1 + e)(1 – cosE)             …. (9)

2 r cos²(f/2) = r(1 + cos f) = r + r cos f =  a(1 – e cosE) + a(cos E – e)

2 r cos²(f/2) =  a – ae cosE + a cosE – ae = a(1 – e) + a cosE (1 - e)

2 r cos²(f/2) = a(1 – e)(1 + cosE)             …. (10)

Compattiamo la (9) e la (10), dividendo la prima per la seconda:

sen²(f/2)/cos²(f/2) = ((1 + e)/(1 – e)) (1 – cosE)/(1 + cosE)

tan²(f/2) = ((1 + e)/(1 – e)) (1 – cosE)/(1 + cosE))     …. (11)

Ancora uno sforzo… non mollate proprio adesso!

Ricordiamoci la (6) e la (7), dove al posto di f inseriamo E (le formule valgono per qualsiasi angolo). Otteniamo:

2 sen²(E/2) = 1 – cos E

2 cos²(E/2) = 1 + cos E

Sostituendo, la (11) diventa:

tan²(f/2) = ((1 + e)/(1 – e)) (sen²(E/2)/cos²(E/2))

tan²(f/2) = ((1 + e)/(1 – e)) tan²(E/2)

Estraendo la radice quadrata, otteniamo, finalmente:

tan (f/2) = ((1 + e)/(1 – e))^1/2 tan (E/2)            …. (12)

La (12) è veramente importante: permette di ricavare l’anomalia vera in funzione dell’anomalia eccentrica, conoscendo, ovviamente, l’eccentricità.

Questo è solo il primo passo del problema di Keplero, dato che l’anomalia eccentrica non può misurarsi. Tuttavia, abbiamo già intuito che essa potrebbe essere collegata all’anomalia media e quest’ultima è di immediata determinazione, dipendendo solo dal periodo orbitale.

Il secondo passo è, allora, quello di legare anomalia eccentrica  e anomalia media. Il genio di Keplero c’è riuscito, anche se ciò che trova non è di facile soluzione e prende proprio il nome di equazione di Keplero. Un'equazione fondamentale che può, però, risolversi solo per approssimazioni successive, un processo, oggi, ridicolo per i calcolatori elettronici. Pensiamo, però, a Keplero che non li aveva ancora...

Precedentemente abbiamo introdotto facilmente il moto medio n. Richiamiamolo velocemente:

n = 2π/P       …. (13)

che non è altro che la velocità angolare media del pianeta, come se fosse inserito in un’orbita circolare.  In realtà, a volte, il pianeta la supera e a volte è più lento, ma al completamento dell’orbita tutto torna al suo posto. Una grandezza facilissima da calcolare e che si ricava dall’area RPS della Fig. 5. che riproponiamo per semplicità.

Si ha subito che n(t – t₀) è l’angolo descritto nell’intervallo di tempo  (t – t₀) da un raggio vettore che ruoti attorno a S con velocità angolare costante n. E’ immediato introdurre una nuova anomalia, detta anomalia media M data da:

M = n(t – t₀)       …. (14)

Da cui, utilizzando la (13) e la (14):

area RPS = πab(t – t₀)/P = 2πab(t – t₀)/2P = n a b (t - t₀)/2 = ½ a b M       …. (15)

Cerchiamo adesso di scrivere quest’area come somma dell’area SRU e dell’area URP, in modo da far comparire l’anomalia eccentrica E).

area RPS = area SRU + area URP       …. (15 a)

Nessun problema per la prima:

area SRU = ½ SU ∙ RU

Tuttavia, sappiamo anche che CS = ae  (Fig. 1)

SU = CU – CS = a cosE – ae

Ricordando la (2. QUI):

RU = r sen f = b sen E

Si ha, in definitiva:

area SRU = ½ (a cos E – ae)(b sen E) = ½ (ab cos E sen E - e ab sen E)

area SRU = ½ ab sen E (cos E – e)      …. (16)

Un po’ più complicato è il calcolo dell’area URP. Per seguire meglio l’operazione usiamo la Fig. 8.

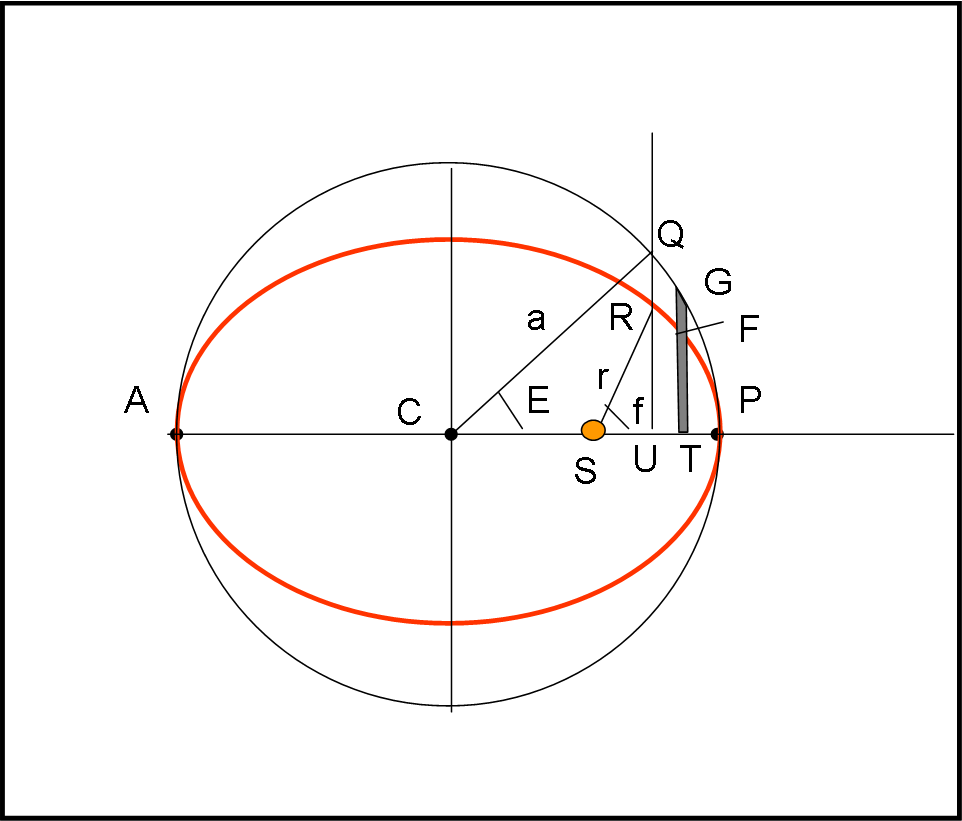
Tracciamo delle strisce di base infinitesima, perpendicolari a PC, che arrivino fino alla circonferenza di raggio CP = a.

Da quanto imparato precedentemente (1), sappiamo che:

QU/RU = a/b

Dato che la base ha una dimensione infinitesima, si ha:

area striscia FT/area striscia GT = b/a

Ne segue che la somma di tutte le strisce  che formano l’area URP (le strisce del tipo FT) deve essere b/a volte la somma di tutte le strisce che formano l’area UQP (le strisce del tipo GT).

In altre parole:

area URP = b/a area UQP

Tuttavia l’area UQP non è altro che l’area del settore circolare CQP meno l’area del triangolo QCU. In parole matematiche:

area URP = b/a area UQP = b/a (area CQP – area QCU)        …. (17)

Tutti dovremmo sapere quanto vale l’area di un  settore circolare… comunque si può ricavare immediatamente attraverso la proporzione:

Area cerchio: 360 = Area settore: angolo al centro del settore.

Nel nostro caso si ha:

πa²/2π = area CQP/E

Ossia:

area CQP = a²E/2

L’area  del triangolo QCU è, ovviamente:

area QCU = ½ QU ∙ CU = ½ a sen E ∙ a cos E = ½ a² sen E cos E

Possiamo tranquillamente scrivere la (17):

area URP = b/a (a² E/2 - a² sen E cos E/2)

area URP = ½ ab (E – sen E cos E)     …. (18)

Non ci resta, adesso, che prendere la (16) e sommarla alla (18) per ottenere l’area di  RPS, come dice la (15a):

area RPS = area SRU + area URP = ½ ab sen E (cos E – e) + ½ ab (E – sen E cos E)

area RPS = ½ ab (sen E cos E – e sen E + E – sen E cos E)

area RPS = ½ ab (E – e sen E)       …. (19)

Ancora un piccolo sforzo, uguagliando la (15) con la (19):

½ ab M = ½ ab (E – e sen E)

M = E – e sen E      …. (20)

La (20) è il risultato di un ragionamento geniale ed è di eccezionale importanza. Essa viene chiamata Equazione di Keplero e permette di legare l’anomalia eccentrica con quella media. Vi invito caldamente di seguire i vari calcoli eseguiti, con molta calma e attenzione. Vi renderete conto della bellezza e armonia del metodo. Un piccolo grande capolavoro geometrico-matematico.

Già sapevamo come ricavare l’anomalia vera dall’anomalia eccentrica e quindi il problema sembrerebbe praticamente risolto: conoscendo l’eccentricità e e l’anomalia media M si può ricavare, attraverso l’anomalia eccentrica E, l’anomalia vera f.  Una vera poesia, un’opera d’arte scientifica…

Tutto risolto? Nemmeno per sogno! Provate a risolvere la (20) per ricavare la E  e vi troverete in grande difficoltà (sia sen E che E sono espressi in radianti). Purtroppo l’equazione di Keplero è un’equazione trascendente e non si può risolvere in modo diretto…

Poco male sia per Keplero che, soprattutto, per le possibilità di calcolo odierne. Basta risolverla  per approssimazioni successive…

Proponiamo un metodo “antico”, ma sempre utile.  Lavoreremo per approssimazioni successive, cercando di arrivare al risultato finale (o almeno avvicinarlo il più possibile) attraverso un processo ripetitivo. Come al solito, vi prego di non “snobbare” questo articolo. Non fatelo per me, ma per Keplero…

Vediamo come si può venire a capo dell’equazione di Keplero. Utilizziamo allo scopo un metodo ben noto in matematica, quello delle approssimazioni successive. Si parte da un valore molto approssimato, si inserisce nell’equazione e se ne trova uno un po’ migliore; lo si inserisce di nuovo e via dicendo fino a ottenere una precisione sufficiente.

Scriviamo la nostra formula in una forma molto più utile, dove l’incognita compaia anche al secondo membro:

E = M + e sin E      …. (21)

Ragioniamoci sopra un attimo. L’eccentricità è generalmente molto piccola per i pianeti (oltre che minore di 1, ovviamente). Moltiplicando un numero (minore di 1 com’è il seno) per un numero molto piccolo (anch’esso minore di 1) si ottiene un numero decisamente più piccolo di quello originale. In poche parole, possiamo considerare come prima approssimazione che (e sen E) sia trascurabile rispetto a M. Scriviamo perciò:

E₀ = M

Non ridiamo… sappiamo benissimo che i due angoli non possono essere uguali, ma il valore così trovato ci serve per migliorare la situazione. Riscriviamo, allora, la (21) inserendo E₀ al posto di E, al secondo membro. Otterremo un nuovo valore approssimato di E che chiamiamo E₁:

E₁ = M + e sen M

Il gioco ci piace e possiamo andare avanti, scrivendo:

E₂ = M + e sen E₁

O, sviluppando E₁:

E₂ = M + e sen(M + e sen M)

Siamo di fronte a una forma:

sen (α + β)

che si risolve, ricordando le formule di addizione che avevamo descritto QUI.

sen(α + β) = sen α cos β + cos α sen β

Nel nostro caso:

E₂ = M + e senM cos (e sen M) + e cos M sen (e sen M)    .... (22)

Soffermiamoci un attimo sopra questa “strana” formula, ricordando sempre che e è molto piccolo.

Ne segue che (e sen M) è molto piccolo e, quindi, il suo seno è praticamente uguale all’angolo, ossia:

sen (e sen M) = e sen M

Tuttavia, se possiamo sostituire il seno con l’angolo, il coseno tende a essere uguale a 1 (raggio del cerchio trigonometrico), come mostra la Fig. 9. Si può allora scrivere:

cos (e sen M) = 1

La relazione precedente diventa:

E₂ = M + e sen M + e cos M ∙ e sen M         …. (23)

Ricordando che:

sen(α + β) = sen α cos β + cos α sen β

e, quindi:

sen (2α) = 2 sen α cos α

sen α cos α = ½ sen (2α)

Nel nostro caso, abbiamo:

cos M ∙ sen M = ½ sen (2M)

Sostituendo nella (23) si ha:

E₂ = M + e sen M + ½ e² sen (2M)

Ovviamente, si può continuare nell'approssimazione inserendo il nuovo valore nella relazione (21), ma il calcolo diventerebbe ripetitivo, oltre che lungo e noioso… Possiamo, perciò, scrivere l’equazione finale che  diventa:

E = M + (e – e³/8) sen M + ½ e² sen 2M + 3/8 e³ sen 3M + …

Con un procedimento analogo si può anche esprimere l’anomalia vera f direttamente in funzione dell’anomalia media. Se ne deriva la seguente relazione:

f = M + (2e - 1/4 e³) sen M + 5/4 e² sen 2M + 13/12 e³ sen 3M + …

Essa viene chiamata equazione del centro.

Per molto tempo, le equazioni precedenti hanno permesso di tabulare, con una precisione del centesimo di grado, i valori di f in funzione di M, per eccentricità inferiori a 0.08.

Oggi, le approssimazioni successive si eseguono in modo rapidissimo attraverso i calcolatori elettronici, ma le equazioni di Keplero sono ancora un segno di genialità e di praticità.

E’ molto difficile trovare questa trattazione nella rete. E’ un po’ come eseguire una radice quadrata… oggi ci pensa direttamente un qualsiasi computer da bambini. La comodità innanzitutto, ma vale la pena sapere che è la mente umana che ha permesso ai calcolatori di fornire le risposte in un batter di ciglio…

Chi ha voglia e curiosità di fare due chiacchiere con Keplero in persona (e non solo lui), può trovarlo QUI