Categorie: Astronomia Elementare Fenomeni astronomici Meccanica Celeste
Tags: congiunzioni fasi lunari fasi planetarie Galileo occultazioni opposizioni
Scritto da: Vincenzo Zappalà
Commenti:3
C’è chi riflette e c’è chi raccoglie: le fasi planetarie **
Questo articolo è stato inserito nella pagina d'archivio dedicata all'Astronomia Classica
Una stella che emette luce e un corpo celeste che la riceve e la riflette danno luogo a situazioni molto variabili per un osservatore posto in una posizione qualsiasi. Stiamo parlando delle “fasi” dei pianeti e dei satelliti del Sistema Solare. Cercheremo di trattare il problema nel modo più generale possibile, non limitandoci ai pianeti interni (come si fa di solito). Data l’importanza di questo argomento, l’articolo verrà inserito, in seguito, anche negli “approfondimenti”.
Analizziamo i vari concetti, quasi sempre considerati separatamente, come risvolti, solo apparentemente diversi, di un unico problema ben più generale. Per far ciò consideriamo tre corpi celesti: il primo è la sorgente di luce, il secondo è il corpo che viene illuminato, il terzo è il corpo su cui è posto l’osservatore.
Limitiamoci alla situazione esistente tra corpi appartenenti a un sistema planetario di una stella singola, come ad esempio quello del Sole.
La sorgente di luce è, allora, proprio il Sole, il corpo illuminato un pianeta o un satellite, quello su cui sta l’osservatore la Terra. Rispetto a quest’ultimo esistono solo due tipi di pianeti: quelli più lontani e quelli più vicini al Sole, ossia quelli esterni e quelli interni. L’unico satellite di una certa importanza per questo problema è il satellite della stessa Terra, ossia la Luna.
Disegniamo, allora, la Fig. 1 dove S è il Sole, V un pianeta interno, M un pianeta esterno, T la Terra e L la Luna.
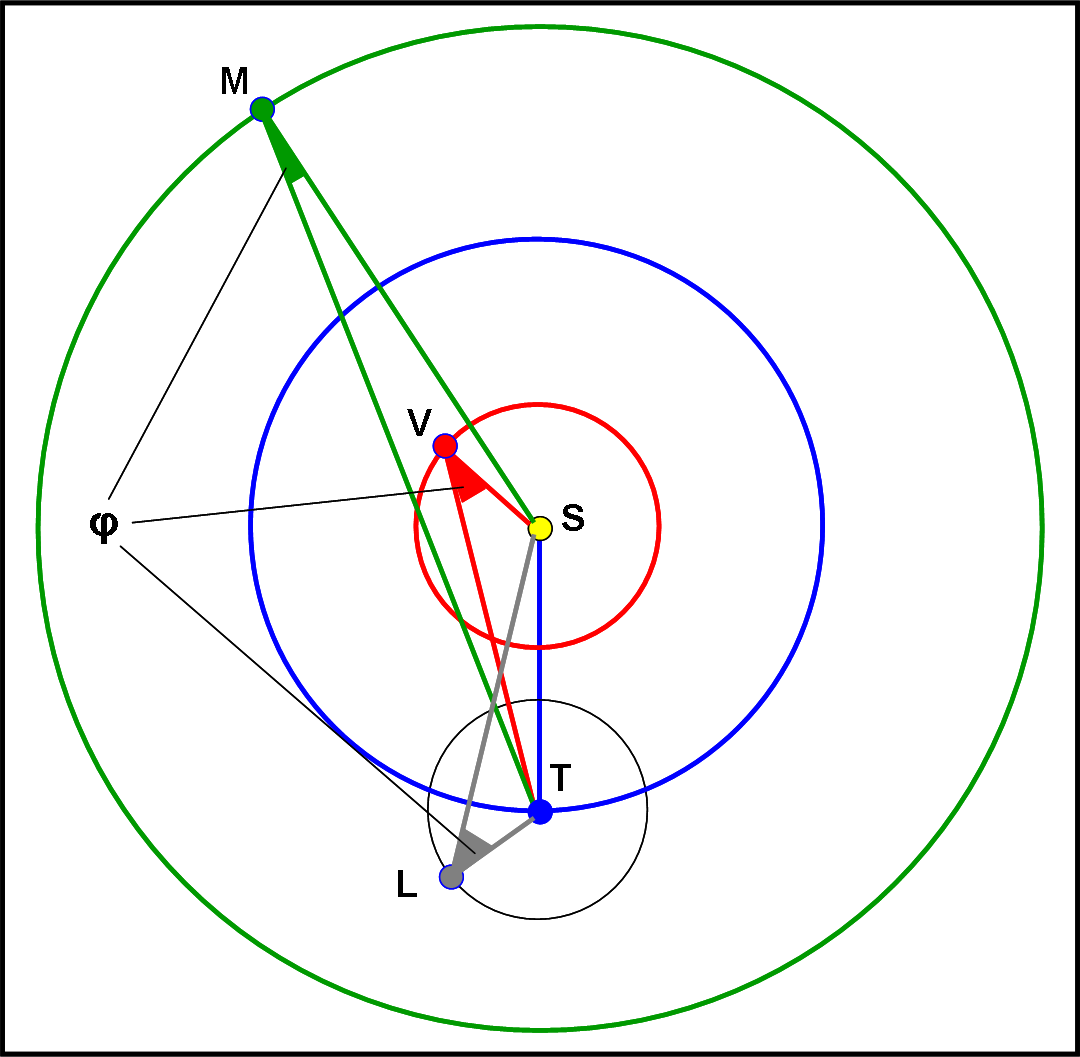
Definiamo come angolo di fase φ l’angolo sotto cui il pianeta o il satellite vede la Terra e il Sole. L’angolo φ indica quindi di quanto sono inclinati i raggi solari che colpiscono il pianeta o il satellite rispetto alla linea di vista. E’ proprio quest’angolo che permette di calcolare l’area della parte illuminata del disco del pianeta o del satellite visto dalla Terra.
Immaginiamo, per semplicità di spiegazione, che tutte le orbite stiano sullo spesso piano e siano circolari.
Delle semplicissime figure ci permettono di ricavare quest’area in funzione dell’angolo di fase per qualsiasi corpo e per qualsiasi posizione esso assuma lungo l’orbita. La situazione è quella rappresentata nella Fig. 2. La luce proveniente dal Sole può essere considerata come un fascio di raggi paralleli tra loro, viste le distanze in gioco rispetto alle dimensioni planetarie.
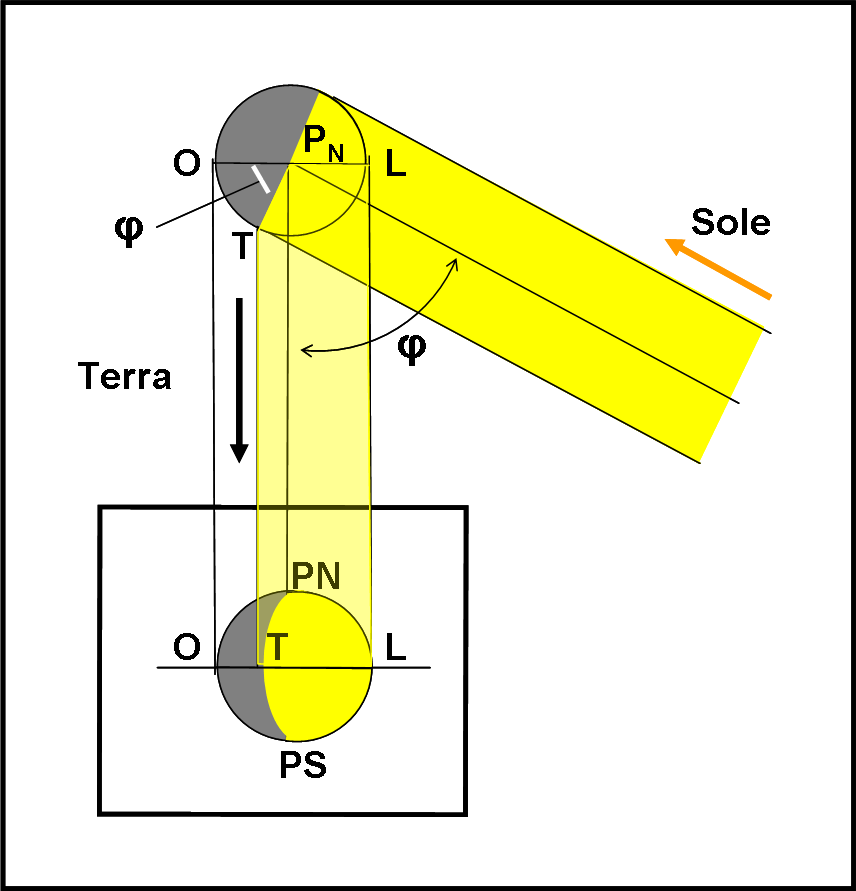
La superficie illuminata riflette la luce ricevuta e solo una parte di questo fascio luminoso colpisce la Terra. L’angolo tra il fascio incidente e quello riflesso è proprio l’angolo di fase φ. E’ immediato comprendere che variando la posizione della Terra (e del pianeta o satellite) varia l’angolo e di conseguenza la “grandezza” del fascio luminoso riflesso che raggiunge l’osservatore.
Banali considerazioni geometriche (angoli formati da rette perpendicolari tra loro sono uguali) ci dicono che OPNT è ancora l’angolo di fase. La parte alta della figura è quella vista perpendicolarmente al piano orbitale; ad esempio, nella direzione del Polo Nord (PN), ma sarebbe analoga la visione dal Polo Sud. Il quadrato in basso rappresenta invece il pianeta visto dalla Terra, ossia nel piano orbitale (la situazione precedente ruotata di novanta gradi). Si notano chiaramente la parte illuminata e quella in ombra, entrambe delimitate da circonferenze e da proiezioni di circonferenze, ossia ellissi.
Per determinare esattamente l’area della parte illuminata ricorriamo alla Fig. 3.
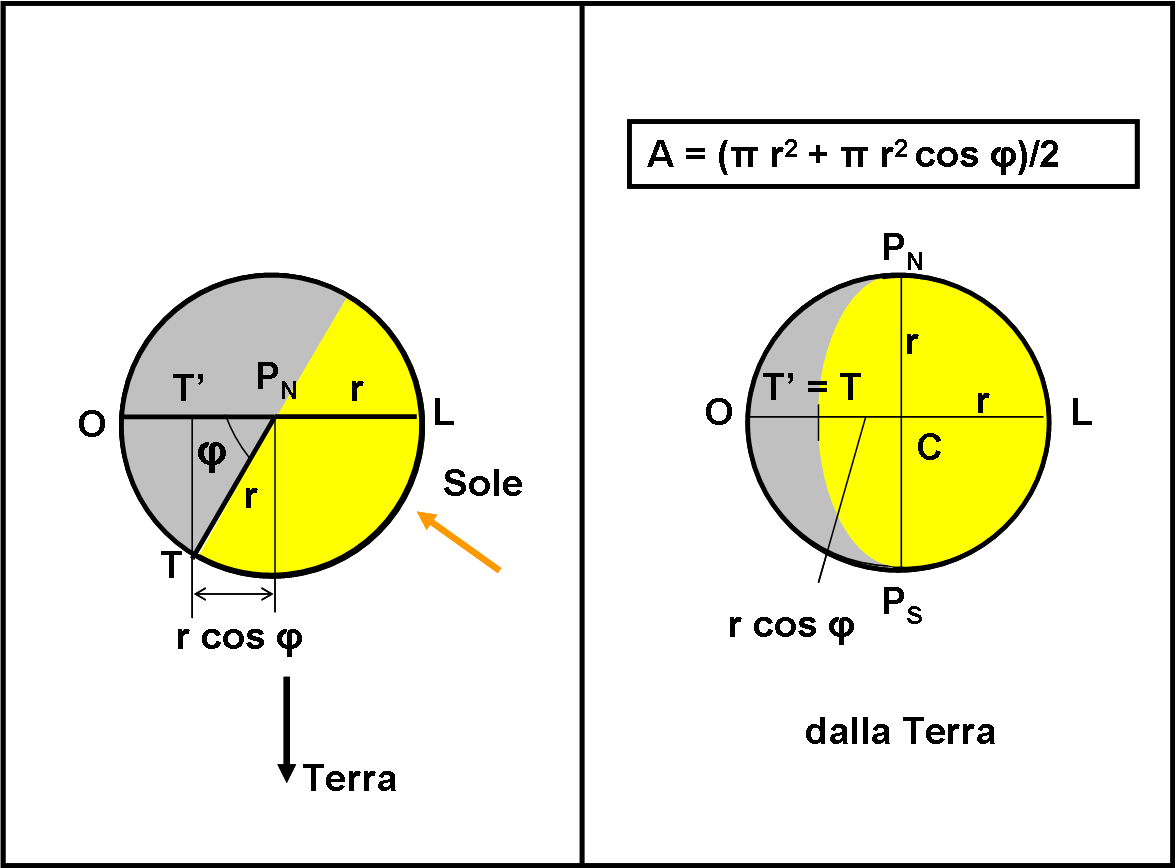
A sinistra la situazione precedente vista nella direzione perpendicolare al piano, nella parte destra il corpo celeste visto dalla Terra. Dal triangolo rettangolo TT’PN si ricava subito:
T’PN = r cos(φ)
Nella visione del disco planetario da terra (parte destra) la lunghezza CT è proprio uguale a T’PN, ossia a r cos(φ).
A questo punto, è immediato determinare l’area della parte illuminata del disco. Essa è data dal semicerchio di raggio r a cui va aggiunta metà dell’ellisse di semiasse maggiore uguale a r e di semiasse minore uguale a r cos(φ). L’area del semicerchio è πr2/2, mentre quella della mezza ellisse è πr2cos(φ)/2 (area ellisse = πab) e quindi l’area illuminata risulta:
A = πr2(1 + cos(φ))/2
Per qualsiasi corpo celeste del sistema solare la formula precedente permette di calcolare l’area illuminata vista da Terra conoscendo soltanto l’angolo di fase e il raggio apparente del corpo.
Normalmente la fase di un pianeta si indica come rapporto tra la parte illuminata e l’area totale. Questo rapporto, che indichiamo con F, si riduce a:
F = A/πr2 = (1 + cos(φ))/2 ……..… (1)
Questa formula “relativa” è molto utile per definire la fase, indipendentemente dalla luminosità apparente del pianeta. Infatti, dobbiamo tenere presente che il raggio r apparente, ossia visto dalla Terra, dipende dalla distanza del pianeta e quindi è variabile lungo tutta l’orbita anche se essa è considerata circolare (si potrebbe anche scrivere la formula che lo definisce in base alla sua distanza dalla Terra).
Per verificare la correttezza della (1) possiamo applicarla ad alcuni casi limite. Per un angolo di fase uguale a 90° si ottiene cos(φ) = 0 e quindi F = 1/2 = 0.5, proprio la metà. Per φ = 0° si ha F = (1 + 1)/ 2 = 1 (il disco visibile è completamente illuminato). Per φ = 180° si ha F = (1 – 1)/2 = 0 (il disco visibile è completamente oscuro).
Finora non abbiamo assolutamente differenziato la trattazione a seconda del tipo di pianeta che si considera o del tipo di satellite. La formula vale per tutti. Quello che cambia è l’intervallo di valori che possono essere raggiunti dall’angolo di fase φ.
Per chi volesse fare un passetto in più, posso dire che il calcolo dell’angolo di fase è altrettanto banale, a patto di sapere le distanze tra pianeta e Terra (Δ) e tra pianeta e Sole (d). Da un qualsiasi triangolo della Fig. 1 (SMT o SLT o SVT) si può ottenere il valore di φ attraverso il teorema di Carnot che permette di conoscere il coseno di un angolo dalle misure dei tre lati di un triangolo qualsiasi, come rappresentato in Fig. 4.
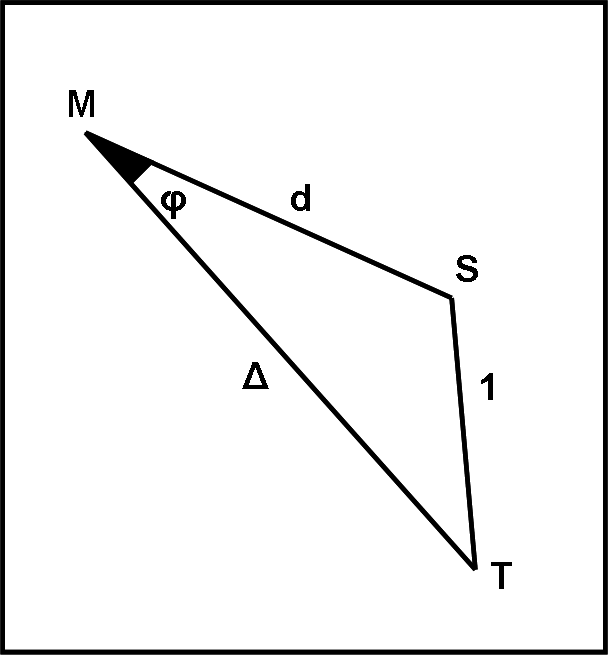
Il teorema di Carnot dice:
ST2 = MS2 + MT2 – 2 MS MT cos(φ)
Ossia:
cos(φ) = (MS2 + MT2 – ST2)/(2 MS MT)
nel nostro caso, esprimendo le distanze in Unità Astronomiche:
ST = 1, MS = d, MT = Δ
E quindi:
cos(φ) = (d2 + Δ2 – 1)/2dΔ
Ovviamente, considerando orbite circolari, d è il semiasse orbitale ed è una costante. Ne consegue che l’angolo di fase dipende soltanto dalla distanza pianeta-Terra. Nel caso della Luna, è invece la distanza Terra-Luna che rimane costante e quindi l’angolo di fase dipende solo dalla distanza Luna-Sole.
Chi ha voglia, e quel minimo di dimestichezza con le funzioni trigonometriche, può divertirsi a calcolare gli intervalli dell’angolo di fase ammissibili per tutti i pianeti del Sistema Solare e dei vari satelliti. La stessa formula, infatti, si può facilmente applicare anche ai satelliti dei pianeti esterni.
Vediamo i casi particolari che più ci interessano di più. Iniziamo da un pianeta interno, come ad esempio Venere (ma le stesse considerazioni possono essere fatte per Mercurio). Esso è rappresentato nella Fig. 5.
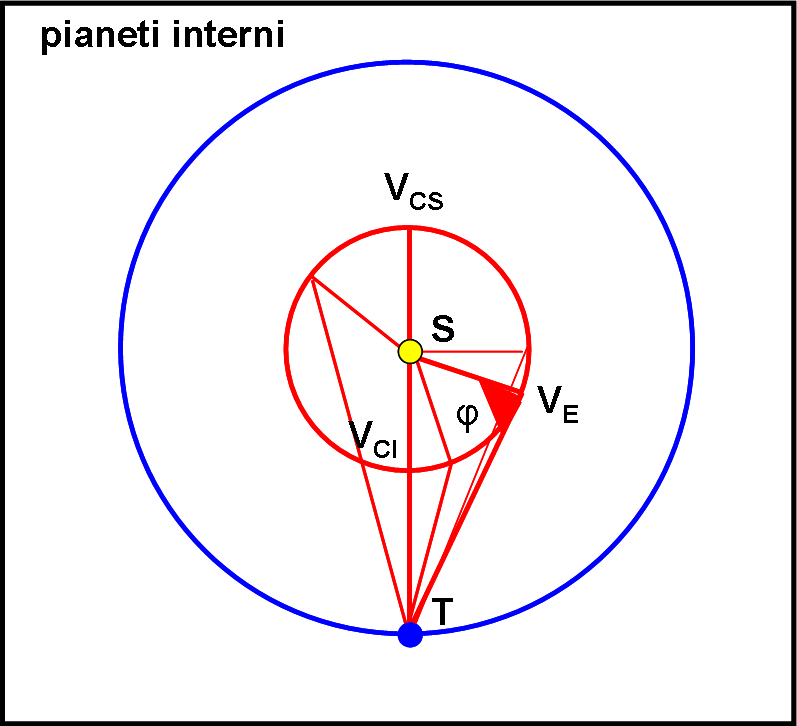
Le configurazioni più importanti si ottengono quando il pianeta si trova esattamente tra la Terra e il Sole e quando si trova esattamente dall’altra parte della stella. Esse vengono chiamate congiunzione inferiore e superiore, rispettivamente. Nel primo caso l’angolo di fase è uguale a 180° e quindi, come visto precedentemente, l’area illuminata vista dalla Terra è ZERO. Nel secondo caso l’angolo φ è uguale a zero e quindi l’area illuminata è uguale all’intero disco.
Particolare importanza ha anche il punto VE. Esso si ricava tracciando la tangente dalla Terra all’orbita di Venere, da cui segue che l’angolo tra le direzioni Venere-Sole e Venere-Terra è esattamente di 90°. Se ne deriva, quindi, che la parte illuminata è la metà del disco totale.
Tuttavia, questo punto ha anche un’altra caratteristica: in esso la distanza apparente tra Venere e il Sole raggiunge il suo valore massimo. In altre parole, in quel punto Venere appare il più lontana possibile dal Sole e si dice che raggiunge l’elongazione massima. Sono queste le condizioni in cui Venere risulta più facilmente visibile prima dell’alba o dopo il tramonto del Sole (posizione speculare di sinistra). Potete facilmente simulare da soli le varie posizioni nel cielo notturno attraverso la semplicissima Fig. 5.
Ovviamente, il fatto che il disco visibile di Venere sia tutto o solo parzialmente illuminato, non vuol dire che la sua luminosità apparente vada di pari passo. Assolutamente no. Infatti, il disco di Venere è completamente visibile quando si trova al di là del Sole (congiunzione superiore), ma la sua distanza è massima e quindi l’area del disco apparente è decisamente più piccola (cambia il raggio apparente del disco). Chi volesse divertirsi ha tutti i mezzi per calcolare qual è la fase che dà la massima luminosità a Venere (bisogna tener conto sia del raggio apparente del disco sia della parte illuminata… buon divertimento!).
Vi invito a provarci da soli, senza ricorrere ai valori già riportati sul web o a quelli forniti dai programmi preparati per gli “sfaticati” o per gli “ignorantelli. In casi come questo, è molto più ripagante ricavare i risultati da soli, capendo ciò che si fa e quindi comprendendo appieno il fenomeno che si sta studiando. Basta solo recuperare la distanza tra Venere e il Sole.
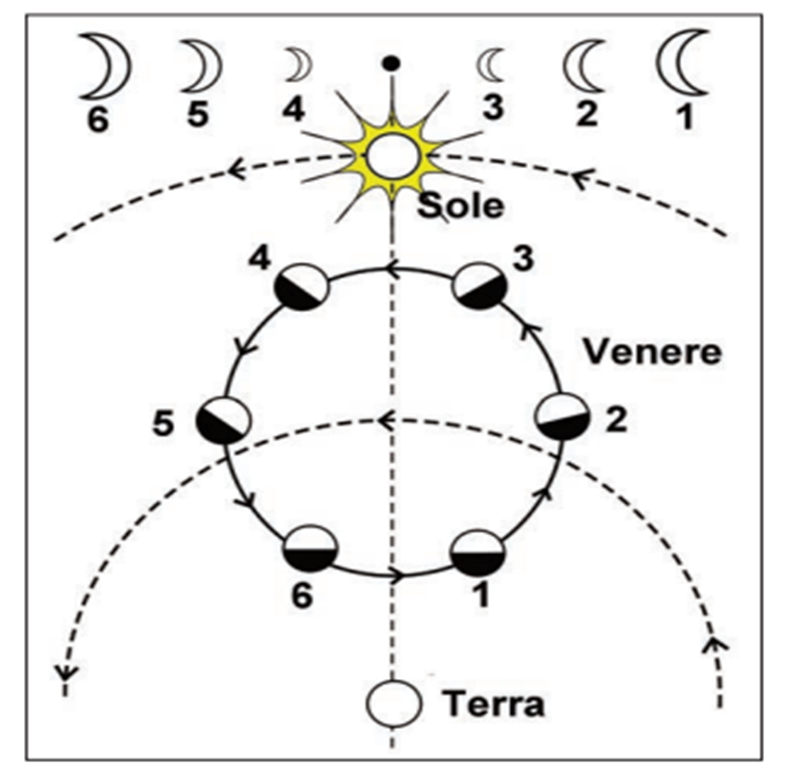
Tanto per darvi fiducia, vediamo in Fig. 6 come il grande Galileo aveva osservato e disegnato le fasi di Venere, un risultato che aveva confermato in modo "praticamente" decisivo il fatto che la Terra doveva girare attorno al Sole al pari di Venere.

Infatti, se avesse avuto ragione Tolomeo la situazione sarebbe stata quella di Fig. 7 e le fasi di Venere sarebbero state completamente diverse!
Tuttavia, la faccenda non era risolta del tutto. Tolomeo era "teoricamente" distrutto, ma non il modello di Brahe che avrebbe permesso delle fasi simili a quelle vere. Personalmente, penso che la Chiesa non abbia mai accettato nemmeno un modello alla Brahe (che ha avuto un seguito molto scarso). Il vero peccato era andare contro Tolomeo e di conseguenza Aristotele. Per la cronaca, la VERA prova arrivò nel 1728 grazie a James Bradley che, cercando di misurare la parallasse delle stelle (intuita da Aristarco di Samo nel III secolo a.C.), scoprì l'aberrazione annua della luce".
Passiamo adesso a un pianeta esterno, ad esempio Marte. Lo schema è riportato in Fig.8. Anche in questo caso le configurazioni principali sono tre, in modo analogo a quanto successo per Venere. Tuttavia, le situazioni sono diverse.
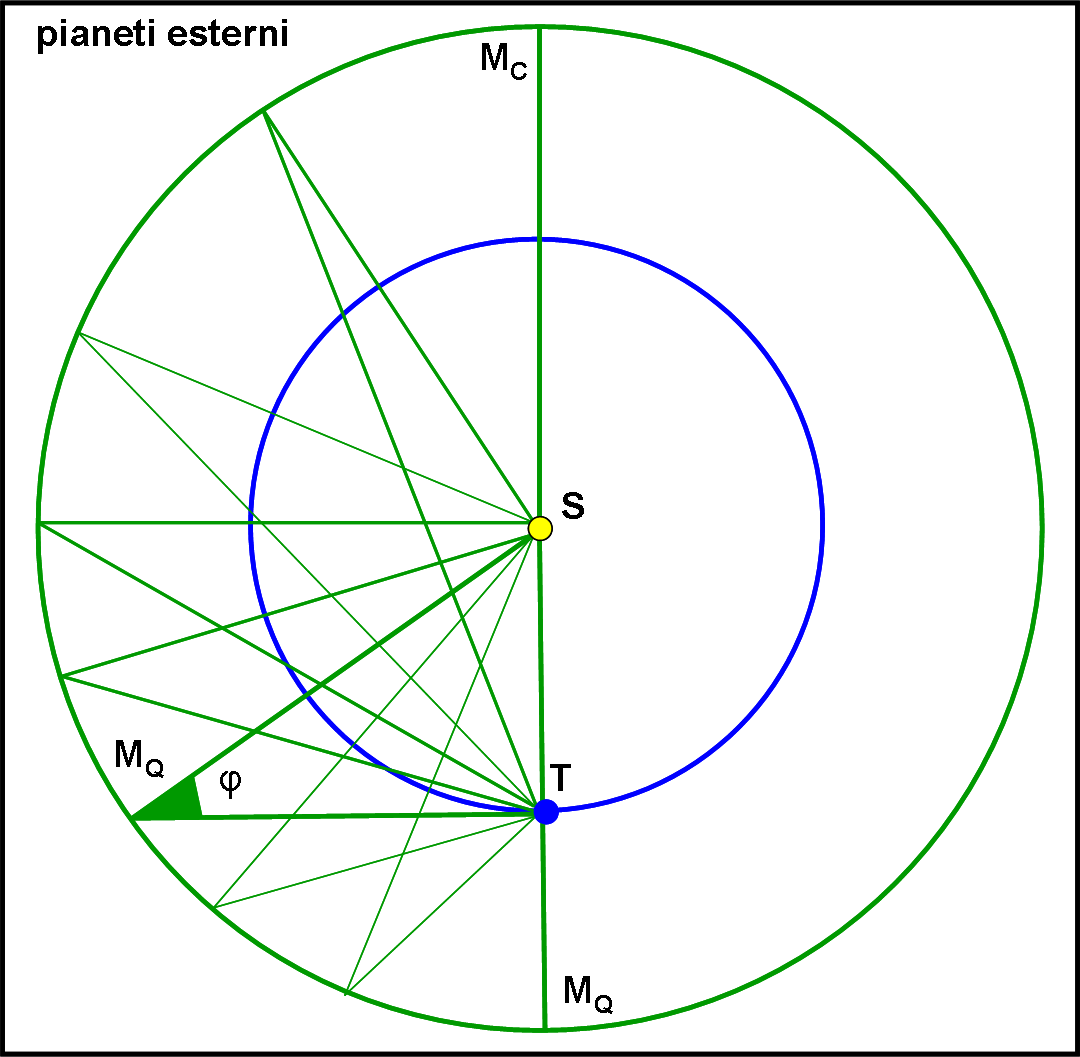
Marte in posizione opposta al Sole porta a un angolo di fase uguale a zero e quindi a un disco completamente illuminato. Tuttavia, questa situazione non è visibile, in quanto Marte scompare nella luce diurna. Più interessante è la posizione con Marte esterna alla Terra rispetto al Sole. Anche in questo caso l’angolo di fase è uguale a zero e quindi il disco è completamente illuminato. Tuttavia, il pianeta è decisamente più vicino (il suo raggio apparente è maggiore) e, inoltre, si vede proprio in piena notte. Questa posizione prende il nome di opposizione.
Infine, va notata la configurazione SMQT, in cui la direzione Terra-Sole e Terra-Marte formano un angolo di 90°. Questa posizione si dice di quadratura ed è relativa al valore minimo della parte illuminata del disco. Ossia l’angolo di fase raggiunge il suo valore massimo. Provare per credere!
Non ci rimane che occuparci della Luna (Fig. 9). In questo caso chi rimane costante è la distanza Terra-Luna. L’angolo di fase raggiunge tutti i valori tra 0 e 180° e porta alle ben note fasi lunari.
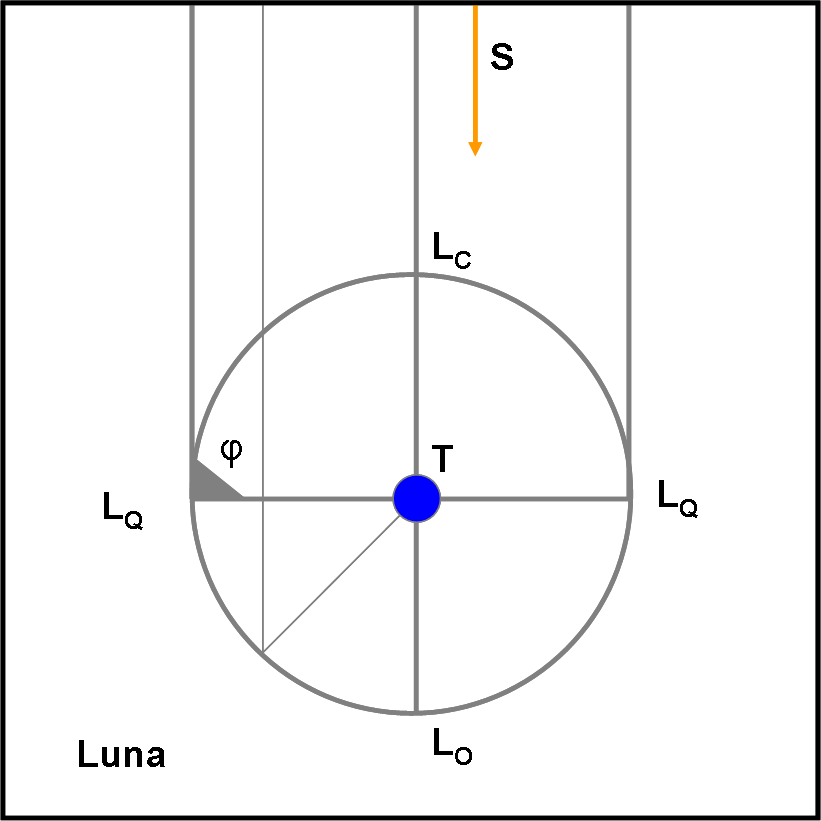
Notate che abbiamo disegnato i raggi provenienti dal Sole tutti paralleli tra loro, dato che il raggio dell’orbita lunare è molto piccolo rispetto alla distanza tra la Terra (e la Luna) e la stella. Non penso ci sia bisogno di evidenziare le fasi lunari. Le potete ricavare da soli studiando la variazione dell’angolo di fase.
Non abbiamo messo in evidenza il caso dei satelliti dei pianeti esterni. In realtà la fase che essi mostrano, se visti dalla Terra, cambia di poco rispetto a quella che hanno i pianeti attorno a cui rivolvono. I satelliti, infatti, sono estremamente vicini ai loro pianeti e la distanza dalla Terra è decisamente maggiore del raggio orbitale. Ne risulta che l’angolo di fase può essere considerato lo stesso di quello del pianeta.
Tutta la trattazione è stata fatta sotto ipotesi restrittive, anche se ancora accettabili per ottenere valori sufficientemente corretti. Dobbiamo, però, ricordare che le orbite dei pianeti non sono complanari, ossia stanno su piani che non coincidono tra loro. Inoltre le traiettorie non sono perfettamente delle circonferenze e quindi il raggio orbitale varia durante la rivoluzione. Tenendo conto di queste particolarità, il calcolo esatto della fase è leggermente più complicato (ma non più di tanto). Questo fatto porta alle grandi opposizioni di Marte (Marte al perielio).
La conseguenza più importante della non complanarità delle orbite comporta, però, che le configurazioni del tipo Sole-Pianeta-Terra o Sole-Terra-Pianeta o Luna-Terra-Sole o Terra-Luna-Sole non sono “quasi” mai delle rette come quelle rappresentate nelle figure precedenti, dove tutto si svolge su un unico piano. Ne deriva una situazione come quella della Fig. 10.
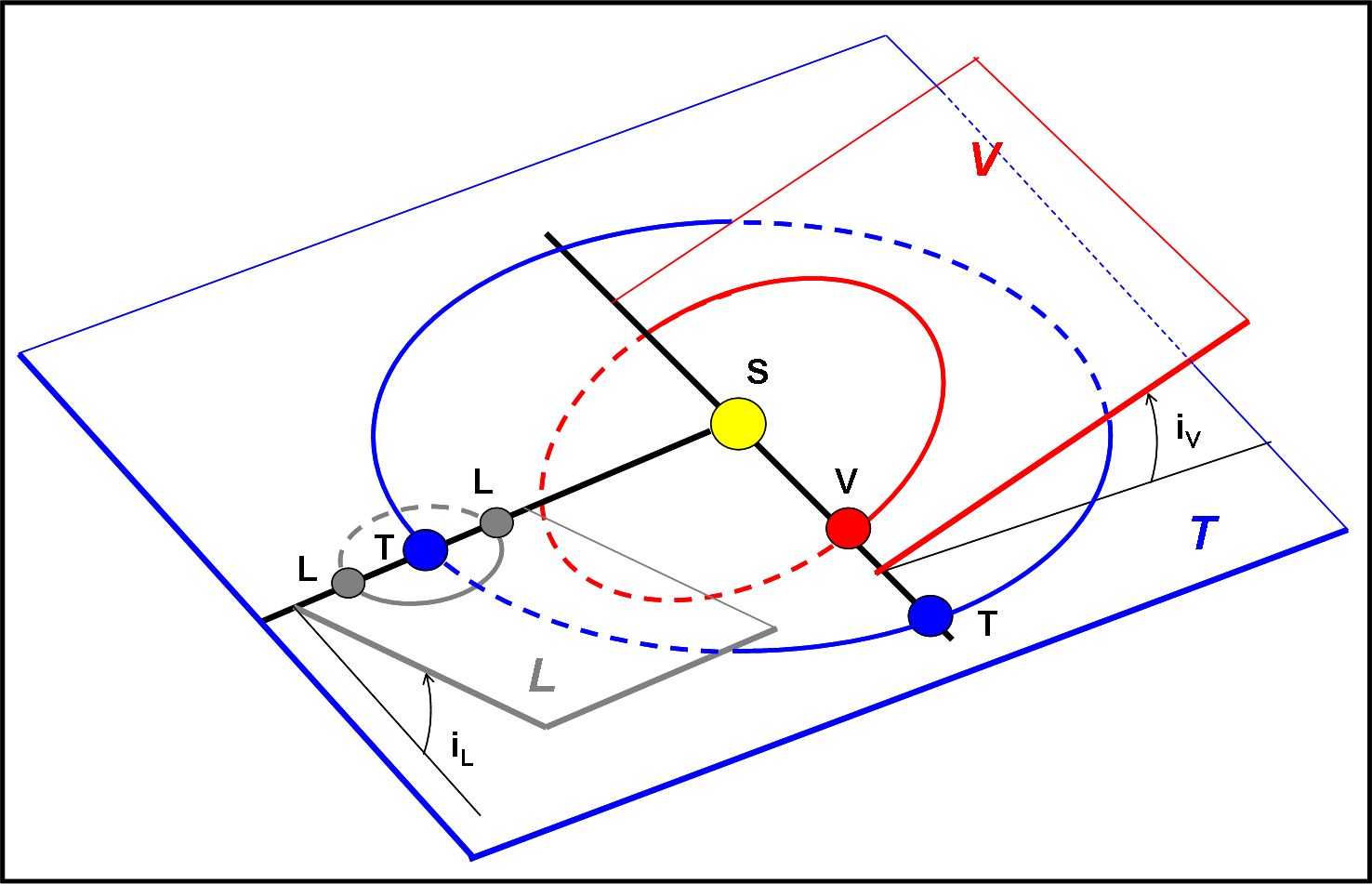
Il piano orbitale della Terra è quello colorato in azzurro, mentre quello di Venere è colorato in rosso e quello della Luna in grigio. Essi formano tra di loro degli angoli non nulli (inclinazioni dell’orbita rispetto all’eclittica). Ne segue che le congiunzioni o le opposizioni non sono “quasi” mai rappresentabili su una sola retta e le direzioni tra i corpi formano angoli normalmente piccoli ma non trascurabili.
Abbiamo detto, però, “quasi” mai.
In realtà, durante le rivoluzioni dei pianeti, della Terra e della Luna, può capitare che il pianeta e la Terra o la Luna e la Terra si trovino entrambi proprio sulla retta che definisce l’intersezione dei piani orbitali. Questa retta si chiama linea dei nodi e indica le uniche possibili posizioni in cui entrambi i corpi celesti (Terra e Luna o Terra e Pianeta) siano su una retta che passa per il Sole. Questa linea, infatti, appartiene a entrambi i piani orbitali, essendone la loro intersezione, e deve, ovviamente, passare per il Sole (cos'è la linea dei nodi, e molto altro, lo trovate QUI)
In questi casi, nascono dei fenomeni particolari legati alle fasi. Si verificano delle OCCULTAZIONI reciproche. Le occultazioni prendono vari nomi a seconda dei corpi celesti coinvolti e si chiamano transiti ed eclissi (ne abbiamo parlato QUI, QUI e QUI). Il concetto è, però, uno e uno solo.







3 commenti
Caro Vincenzo, seguo sempre con tanto interesse i vostri articoli nel desiderio di saperne di più, ed inevitabilmente capita di avere qualche cosa da chiederti. In questo caso, trattasi del fenomeno della luna a barchetta e del motivo per cui è possibile osservarlo bene solo a certe latitudini. Qua e là in rete ho trovato cose che mi hanno confuso solo le idee. Ho letto che è possibile stabilirne la data, è un fenomeno soggettivo e può essere anche rovesciata. E' possibile osservarla anche in Italia?
Un caro saluto
Walter
caro Walter,
ti ringrazio per la domanda in quanto mi ha permesso di verificare che non avevo mai pubblicato un articolo su quell'argomento. Ero convinto di sì e, invece, era sul vecchio sito... Entro oggi lo pubblicherò anche qui e spero ti sappia rispondere adeguatamente.
Grazie infinite!!
E io ringrazio Walter perché, grazie al suo commento, mi sono accorto che questo bell'articolo non era stato inserito in archivio... ma ho già rimediato (e, zitto zitto, tanto per farmi un po' di pubblicità, ci ho messo anche una ricostruzione delle fasi della Terra ripresa dai miei astericci)