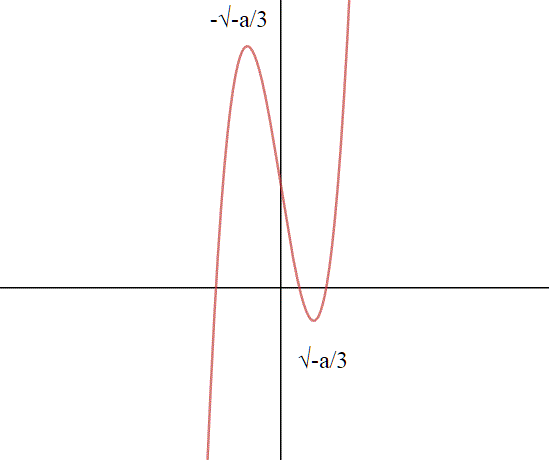Il quiz è stato presentato QUI.

Intanto grazie della partecipazione; tutti i partecipanti hanno intuito i legame fra l'isola e l'espressione ; molto originale la soluzione di Fabrizio  che trovate qui. Mi discosto un po' dalla sua soluzione che comunque vi invito a leggere, per darne un'altra, che assomiglia di più a quella di Maurizio.

Non ci conviene studiare gli zeri della curva ellittica, ma quelli della funzione polinomiale:

Infatti la curva si annulla se e solo se si annulla tale polinomio:

Studiamo tale funzione con i metodi dell'analisi matematica; calcoliamo la derivata prima

;

affinchè sia possibile risolvere tale equazione , deve essere ; se a>0 g(x)  è sempre crescente, quindi solo una soluzione; in tal caso risulta anche  .

Se a=0,   abbiamo tre soluzioni coincidenti.

vediamo il caso in cui a<0 e , per l'annullarsi della derivata prima abbiamo due valori:

  , la funzione f(x) decresce strettamente in  e cresce strettamente altrove; in

ha un massimo, in un minimo;infatti il limite per x tendente a meno infinito è meno infinito, per x tendente a più infinito più infinito:

 ; 

Se nel punto di minimo la funzione è negativa , e se nel punto di massimo la funzione è positiva, allora essendo continua avremo tre soluzioni.

sostituiamo quindi nella funzione:

il valore     otteniamo:

notiamo che:

dovrei infatti prendere , ma la radice di sinistra è positiva, essendo a negativo scarto quella con il +a.

quindi:

dunque deve essere

analogamente, sostituendo la radice negativa avremo:

Il fatto che quando l'espressione  è positiva non ci sia l'isola, ci potrebbe indurre a pensare che l'isola ci sia quando l'espressione  è negativa. Qualcuno infatti senza far nessun calcolo lo ha intuito subito.

Vogliamo adesso provare come le due condizioni siano strettamente legate all'espressione:

.

Supponiamo che ;

allora:

ciò è possibile se:

questo significa:

 (punto di massimo)

 (punto di minimo)

In questo caso le soluzioni sono tre. Quindi  la condizione:

unitamente al fatto che a<0 è sufficiente per creare l'isola. Nei casi in cui invece non c'è l'isola, o il massimo è negativo, oppure il minimo è positivo.

Nel caso che il minimo sia zero,  avremo:

ovvero 

ma 

se elevo al quadrato ottengo:

ovvero

se qualcuno ha letto questo articolo questa è proprio la condizione di singolarità: abbiamo un nodo.

 

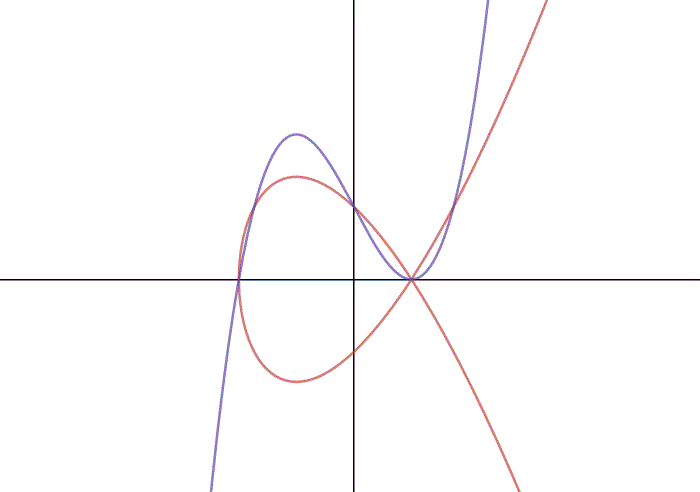
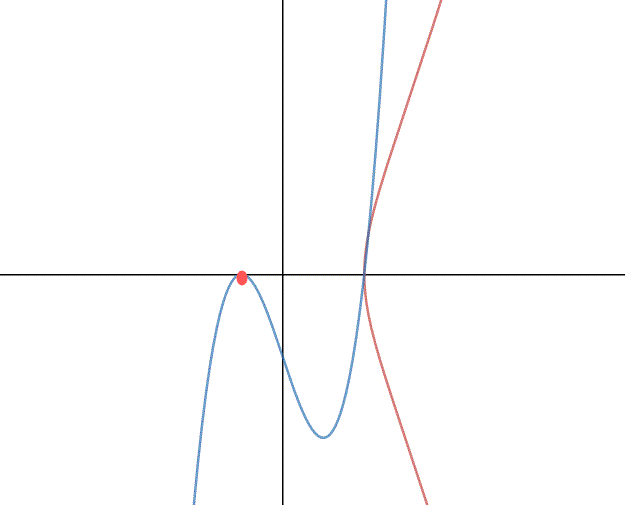
Nel caso invece che sia il massimo nullo, vediamo graficamente che abbiamo due soluzioni;la situazione è questa;L'isola si riduce a un punto! Ance in questo caso .

Riassumiamo graficamente gli altri casi:

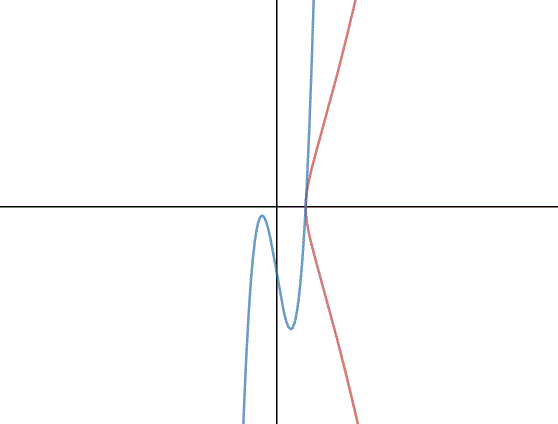
minimo negativo massimo positivo:

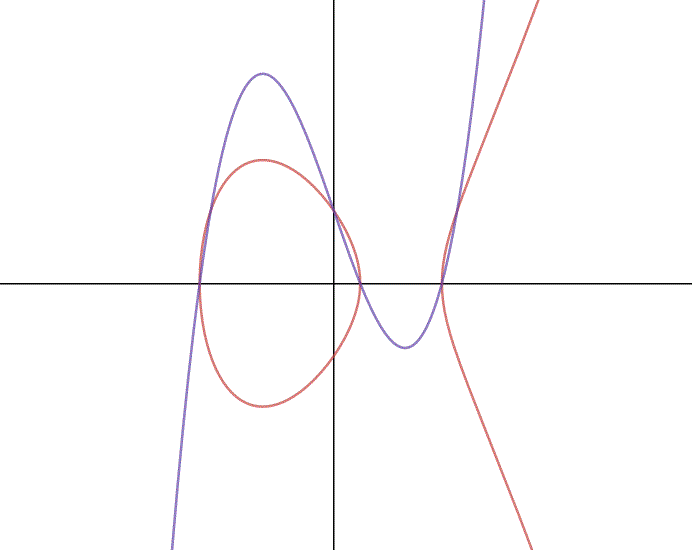
minimo positivo:

 

massimo negativo

 

QUI tutti i quiz del club dei maghi, QUI tutti i quiz del blog