Categorie: Matematica Teoria degli insiemi
Tags: curve ellittiche matematiche superiori
Scritto da: Umberto Cibien
Commenti:2
Matematiche pure 9: Il gruppo delle curve ellittiche, parte prima.
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica
Riprendiamo il discorso sulle curve ellittiche; nell' articolo precedente (qui), abbiamo trovato il punto all'infinito di una curva ellittica di equazione generica: ; esso coincide con il punto all'infinito dell'asse delle y; questo ci fa capire che la curva all'infinito è tangente all'asse delle y. Adesso volevo evidenziare meglio il fatto che la curva ellittica non è una funzione ma un luogo geometrico di punti. Una funzione infatti per ogni valore della x ha un solo valore dell y; si vede anche dal grafico che nel caso delle curve ellittiche ciò non è vero sempre.
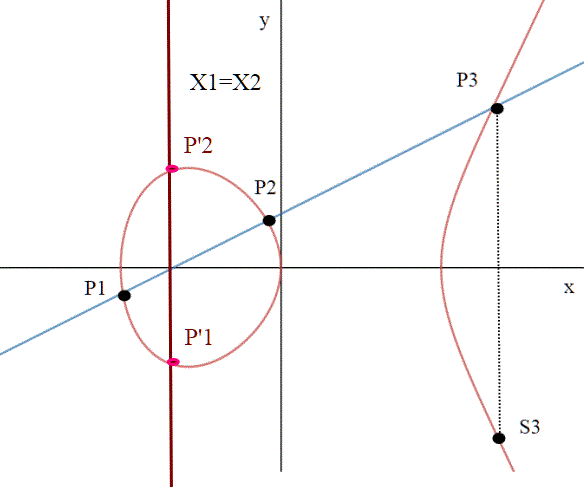
L'operazione che abbiamo definito sui punti della curva , che dati due punti trova il risultato S3 come indicato nel disegno, è valida sia nel caso che la retta passi per due punti distinti, oppure sia verticale (il punto diventa il punto improprio o punto all'infinito). Nel quiz sulle curve ellittiche (qui) abbiamo fatto in dettaglio i calcoli nel caso x1<>x2 per trovare il terzo punto S3; Nel caso la retta per P1,P2 sia verticale sappiamo che il punto è
; ci manca da trovare il punto nel caso P1=P2 e y1=y2, ovvero quando la retta è tangente alla curva. Ma procediamo per gradi.
Le funzioni implicite.
Le curve ellittiche sono un esempio di funzioni definite implicitamente . Ma per capirlo meglio, cominciamo da un caso più semplice; una circonferenza con centro nell'origine e di raggio unitario.
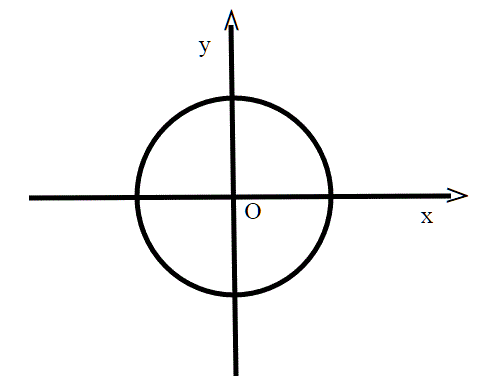
Come tutti sappiamo, tale circonferenza ha equazione . Ma guardiamo adesso la cosa da un punto di vista diverso; consideriamo la funzione di due variabili:
; tale funzione è definita su tutto R x R--->R. Consideriamo adesso solo i valori per cui F(x,y)=0; Tali valori definiscono proprio la circonferenza di sopra. Infatti:
cioè
. Cosa vuol dire questo discorso? Che data una funzione di due variabili,i punti in cui la funzione si annulla definiscono un luogo geometrico, che può essere o meno una curva.
Ci chiediamo se, almeno localmente, tutte le soluzioni dell’equazione F(x, y) = 0 si possono rappresentare tramite una funzione della sola x oppure tramite una funzione della sola y, ovvero se esiste una funzione f tale che F(x, f(x)) = 0 o esiste una funzione g tale che F(g(y), y) = 0. Torniamo alla nostra circonferenza, e consideriamo il punto P(0,1) che vi appartiene, e che quindi è soluzione dell'equazione F(x,y)=0
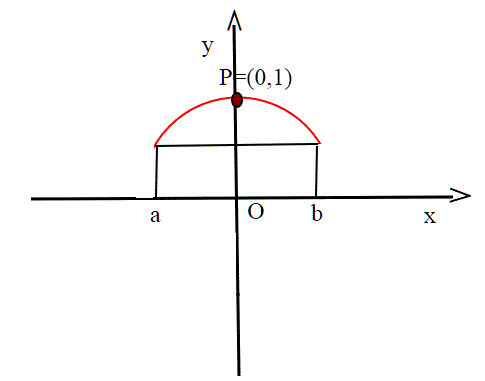
Possiamo, attorno al punto, possiamo rappresentare localmente le soluzioni tramite i punti del tipo , quindi in questo caso f sarà proprio
. Possiamo dire dunque che F(x,y) definisce in modo implicito una funzione f(x) . Questo naturalmente accade sotto determinate condizioni; nel caso sopra sappiamo che nell'intervallo (a,b) y è sempre positiva, quindi per risolvere l'equazione
possiamo prendere solo la radice positiva, e ottenere proprio
.
Trovare la derivata di una funzione definita implicitamente
Supponiamo adesso di dover trovare la tangente alla circonferenza in un punto P; supponiamo :
.

Ci sono più metodi per trovare il coefficiente angolare della retta tangente in quel punto, ma questo probabilmente non lo avete mai visto. Sappiamo che sulla circonferenza:
; quello che noi dobbiamo trovare è il rapporto
; deriviamo rispetto a x ambo i termini della 1. :
; Il termine di sinistra è la derivata della funzione composta
.
Ricordiamo che la derivata di una funzione composta è data da:
f(g(x))'=f'(g(x))* g'(x)
quindi ;
; quindi se
come nel nostro caso, tale derivata o coefficiente angolare vale -1. Questo metodo è un po' brutale, ma evita di dovere parlare del Teorema del Dini sulle funzioni implicite la cui dimostrazione è fuori portata. E' da notare poi che questa espressione (
) non ci dà una funzione esplicitata, ma solo un metodo di calcolo per trovare la derivata di una funzione definita implicitamente in un punto.
Calcolo della tangente ad una curva ellittica
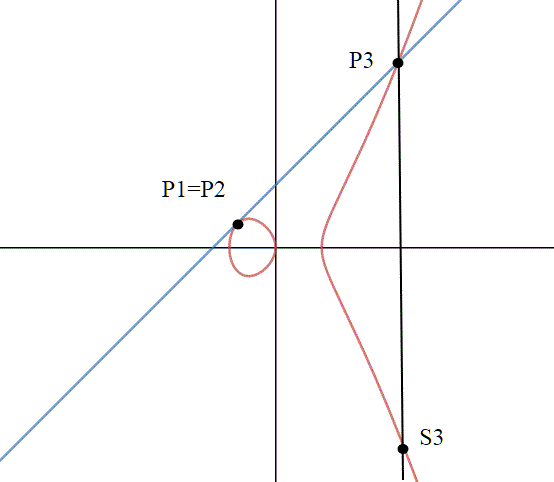
Torniamo adesso alle nostre ellittiche; Per la definizione di somma resta fuori il caso in cui P1=P2,ovvero la retta è tangente. Escludiamo per adesso il caso in cui tale tangente sia parallela all'asse delle y, ovvero sia verticale. Possiamo allora applicare lo stesso metodo che abbiamo applicato alla circonferenza.
; derivando ambo i membri rispetto a x:
; supponiamo che y<>0; abbiamo allora.
: se vogliamo adesso il coefficiente angolare della retta in P1, basta che sostituiamo le sue coordinate:
. e abbiamo finito.
Se y1=0, la retta tangente è verticale; in tal caso si definisce in questo caso P1+P1=.
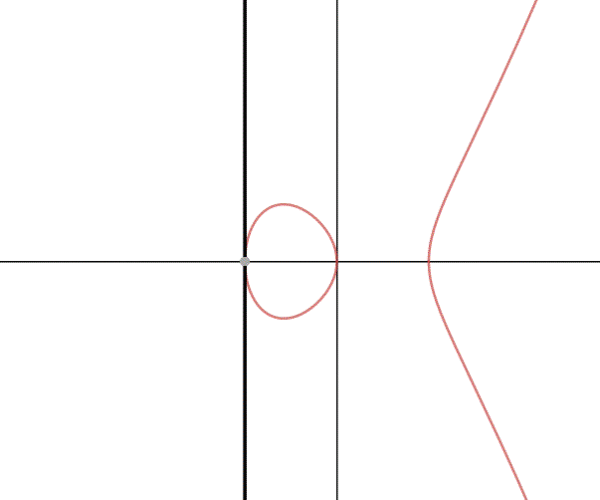
La tangente interseca infatti la curva in ; se da lì tracciamo la retta per
e
otteniamo ancora
.
Ci chiediamo ora una cosa; questa tangente esiste sempre? La sua espressione è(coefficiente angolare):
: se y=0 abbiamo visto che la tangente è parallela all'asse delle y. Ma allora in quale caso perde di significato? Bè, quando si annullano contemporaneamente numeratore e denominatore.
Quindi y=0, . ma se y=0, allora anche
moltiplichiamo la prima equazione per 3 e la seconda per x:
sottraendo membro a membro otteniamo:
sostituiamo adesso il valore di x nella ottenendo:
; quindi
1)
I punti in cui succede questo si dicono singolari e le curve per cui vale la 1) sono dette anch'esse singolari. Questa espressione è anche detta discriminante della curva ellittica.
Esempi di curve singolari.
; nel punto 1 ha una radice doppia e la curva ha una singolarità;
infatti ,
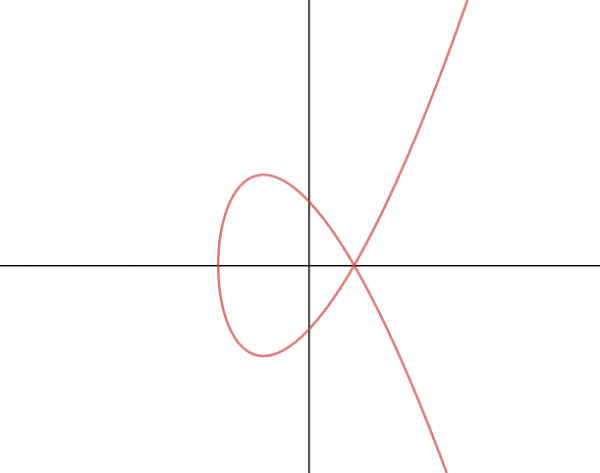
Una curva di questo tipo è detta nodo.
; In questo caso la radice doppia è in zero, anzi è addirittura tripla.
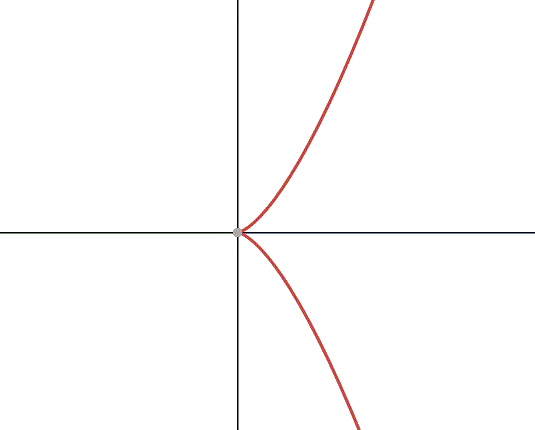
Una curva di questo tipo si dice cuspide.
Per avere un gruppo, ovvero affinchè sia sempre possibile trovare P+Q, la curva deve quindi soddisfare la condizione
.
Nel prossimo articolo faremo un riassunto tutto quello che è stato fatto sulle curve ellittiche, e arriveremo a dimostrare che con l'operazione di somma descritta ogni curva forma un gruppo.






2 commenti
Buongiorno, faccio notare che il punto:
non appartiene alla circonferenza di equazione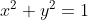 .
.
Buon lavoro.
Dott. Landolina Paolo
ha ragione. si intendeva chiaramente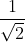 ; appena riesco a trovare l'articolo lo correggo.
; appena riesco a trovare l'articolo lo correggo.
Sa, è roba di qualche anno fa. comunque grazie della segnalazione.