Categorie: Matematica Teoria degli insiemi
Tags: curve ellittiche matematiche superiori
Scritto da: Umberto Cibien
Commenti:12
Matematiche pure 8): I punti impropri della geometria proiettiva
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica
Nel quiz sulle curve ellittiche , che trovate qui e qui, abbiamo introdotto una operazione interna fra i punti di tali curve. L'equazione generale di una curva ellittica è la seguente:
Prossimo nostro obiettivo sarà quello di dimostrare che con questa operazione i punti della curva formano un gruppo, se aggiungiamo però a tale insieme un punto che non è nel piano , anche se appartiene alla curva. Tale punto è detto "punto all'infinito". Ricordo brevemente come abbiamo definito l'operazione: si considerano due punti della curva (che possono anche coincidere) e si traccia la retta per quei due punti (nel caso coincidano è la tangente); detto P3 il terzo punto in qui la retta incontra la curva (e abbiamo dimostrato che esiste ), costruiamo il simmetrico rispetto all'asse delle x; tale punto è il risultato dell'operazione. Tutto questo è valido se x1<>x2 ; nel caso x1=x2 (e ) la retta diventa parallela all'asse delle y e sembra non intersecare più la curva. In realtà possiamo pensare che la intersechi all'infinito
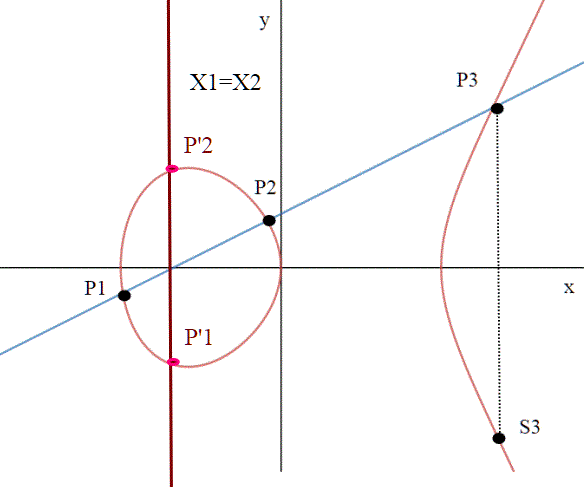
I punti all'infinito della geometria proiettiva
La geometria proiettiva nasce dall'esigenza di unificare determinati discorsi in ambito geometrico; succede infatti di trattare delle dimostrazioni la cui soluzione può ad esempio dipendere dall'intersezione fra due rette; sappiamo che due rette si intersecano se non sono parallele, quindi all'interno di determinate dimostrazioni dovremmo distinguere una casistica, e ciò in matematica non va bene. Si supera lo scoglio passando ad un altro tipo di piano, detto proiettivo, in cui due rette hanno sempre intersezione, anche se sono parallele. Tali punti di intersezione si dicono punti impropri.
Comincio il discorso sui punti impropri delle geometria proiettiva servendomi di un articolo molto bello sui punti all'infinito nel piano ,che potete trovare QUI. Consiglio di leggerlo per chi affronta per la prima volta questo tipo di discorsi. Riassumendo in poche parole tale articolo, dall'osservazione che rette parallele in realtà prospetticamente si incontrano all'orizzonte in un punto e che diverse coppie di rette parallele si incontrano sempre all'infinito ma in punti distinti, possiamo introdurre una nuova categoria di punti, detti punti impropri, che altro non rappresentano che la direzione di tali rette. Procedendo in tale modo, anche le rette parallele avranno una intersezione; tale intersezione è proprio un punto improprio
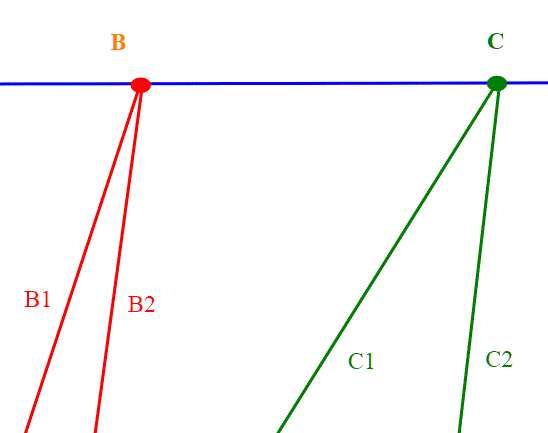
Le rette B1 e B2 sono parallele; prospetticamente parlando si intersecano in un punto B all'infinito; C1 e C2 sono anch'esse parallele, ma non a B1, B2; si intersecano in un altro punto C; i punti B e C si trovano su una retta detta retta impropria.
Un breve discorso sulle dimensioni
In matematica, non esiste una definizione di dimensione che comprenda adeguatamente tutte le situazioni in cui vorremmo farne uso. Si supera il concetto quando si parla di spazio vettoriale, che noi però non abbiamo trattato.
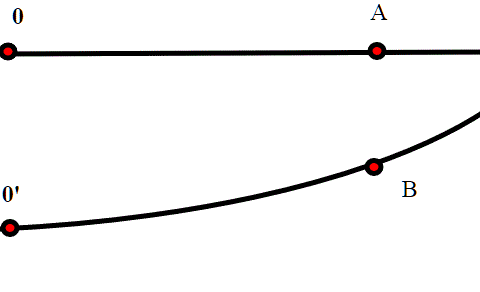
Possiamo però pensare alla dimensione usando le coordinate; per individuare un punto sulla retta basta una coordinata (fissato O altro non è che la distanza OA); si dirà in questo caso che la retta ha dimensione 1. Possiamo però estendere questo discorso anche ad una linea curva; stabilendo una origine, possiamo individuare il punto con una coordinata (detta curvilinea) che altro non è che la lunghezza dell'arco OB. Nel piano servono due coordinate per individuare un punto; qui abbiamo dimensione 2.

esistono anche qui altri oggetti con dimensione due; in una superficie si possono infatti trattare coordinate curvilinee; anche qui servono due coordinate per individuare un punto. La dimensione di un oggetto geometrico è quindi il numero minimo di coordinate che servono per individuare un suo punto.
Le coordinate proiettive: La retta proiettiva
Consideriamo le coppie del piano R x R, escludendo (0,0); sappiamo cosa rappresenta una coppia (X,Y);
Un vettore che parte da (0,0) e arriva in (X,Y). Consideriamo i vettori con coordinate proporzionali ovvero vettori del tipo (X,Y), (λX,λY) con λ<>0. Tutti tali vettori hanno in comune la direzione . Possiamo vederlo dal fatto che formano triangoli simili:

Ricordate le relazioni d'equivalenza? Le abbiamo trattate qui. A mio avviso sono il modo più completo per introdurre gli spazi proiettivi.
Definiamo una relazione d'equivalenza in R x R, (con (X;Y)(0,0) in questo modo:
se (e solo se)
;
Per vedere che è una relazione d'equivalenza dobbiamo verificare che:
- è riflessiva
- è simmetrica
- è transitiva
per dimostrare la 1 : (X,Y)=
2 : se e
,
3: se e
allora
l'insieme delle classi di equivalenza (insieme quoziente) si chiama retta proiettiva e si indica con . Possiamo pensare di identificare tutte le direzioni con i punti di un cerchio di raggio unitario centrato nell'origine:

l'insieme di tutte le direzioni corrisponde proprio ai punti sul cerchio (considerando uguali quelli antipodali; qui stiamo parlando di direzione, non ci interessa il verso). Ecco perchè abbiamo escluso in punto (0,0); il vettore nullo non individua nessuna direzione.
Il punto (1,2) ha indifferentemente coordinate (1,2), (2,4), (-1,-2,), (-2,-4) ecc. Tali coordinate prendono il nome di coordinate proiettive omogenee. Se adesso pensiamo di dividere la prima coordinata per la seconda otteniamo 1/2 in ogni caso. In generale tutte le coppie (X,Y) se Y0 possono essere identificate con (X/Y,1); quindi ogni punto può essere identificato da (K,1)(che quindi è un oggetto geometrico di dimensione 1) .Questo genera una corrispondenza biunivoca fra
privato del punto (X,0) e la retta reale. Nella retta R ogni punto può essere individuato solo da X; questa si chiama semplicemente coordinata, come sappiamo. Riassumendo:
- Spazio proiettivo
; ogni punto viene individuato da due coordinate dette proiettive omogenee
- Retta reale R; per individuare un punto basta una coordinata. Tale coordinata di solito si chiama coordinata affine, o non omogenea.
esiste una corrispondenza biunivoca fra in cui escludiamo il punto(X,0) e la retta R. Si può pensare di estendere questa corrispondenza a tutto
in tal modo ; aggiungendo a R un punto , detto punto infinito. Quindi
.Tale infinito salta fuori, intuitivamente, da una divisione per zero.
Il piano proiettivo
Consideriamo adesso l'insieme R x R x R, ovvero delle terne di numeri reali (X,Y,Z) supponiamo inoltre che (X,Y,Z)(0,0,0).Tutti i vettori (punti) uscenti dall'origine individuano una direzione .Escludiamo il vettore nullo perchè non individua nessuna direzione. Definiamo una relazione in tal modo:
se (e solo se)
,
.Questa è ancora una relazione d'equivalenza, come nel caso precedente di R x R.
La classe di equivalenza di questa relazione è costituita dalle terne con coordinate proporzionali; tale classe prende il nome di punto proiettivo. Per rappresentare la classe , sappiamo che possiamo prendere qualsiasi rappresentante; per esempio (6,4,18) , (12,8,36) , (3,2,9) sono tutte terne equivalenti.
Si definisce piano proiettivo , e si indica con l'insieme quoziente di tale relazione d'equivalenza, ovvero l'insieme di tutte le classi.
Consideriamo adesso le terne (X,Y,Z) dove Z0; possiamo dividere per Z (ovvero moltiplicare per 1/Z);
(N.B. : abbiamo diviso per Y, supponendo Y0; questa è una scelta arbitraria, avremmo potuto dividere per X o per Y e il succo del discorso non cambierebbe. E' solo una scelta di notazione.)
la terna (X/Z,Y/Z,1) è equivalente alla terna (X,Y,Z). Poniamo adesso X/Z=K, Y/Z=K'e otteniamo che il generico punto (con Z0) può essere indicato con (K,K',1). La generica terna di questo tipo è in corrispondenza biunivoca con R x R; questo tipo di punti si chiamano "punti finiti" o "punti propri" e corrisponde in pratica al nostro piano usuale. Questo oggetto geometrico ha dimensione quindi 2.Per ottenere tutto il piano proiettivo, ai punti finiti vanno aggiunti quindi soltanto i punti con Z = 0. Se Z = 0 le classi di equivalenza che si ottengono sono del tipo [X ,Y , 0] con X e Y non entrambi nulli: il loro insieme si identifica* pertanto con la retta proiettiva P1(R ) e viene detto retta all’ infinito e i suoi punti [X , Y , 0] sono detti punti all’ infinito. Possiamo concludere che il piano proiettivo altro non è che l'unione del piano usuale con la retta all'infinito.
*(infatti ,se Z=0, se e solo se
e questo se e solo se
; ma questo identifica la retta proiettiva.)
Per concludere questo breve discorso, vediamo che il piano proiettivo è un oggetto un po' strano. Di solito uno oggetto geometrico è l'insieme dei suoi punti; qui , invece è anche l'unione di un piano (spazio di dimensione 2) con una retta (spazio di dimensione 1) che sono insiemi disgiunti. Abbiamo formalizzato in pratica ciò che si intuiva dalla figura 1:

Piano proiettivo e piano affine
Tanto per puntualizzare ed evitare confusione nei prossimi discorsi: il piano proiettivo è l'insieme di tutti i punti con coordinate proiettive (classi della relazione di equivalenza); certi punti si possono anche esprimere con coordinate non omogenee, o affini. Sono i punti usuali di R x R, che possiamo identificare anche con il piano Euclideo. Tale piano prende anche il nome di piano affine. Nel piano proiettivo abbiamo in più i punti impropri, quelli con coordinata omogenea Z=0, che non possiamo trasformare con coordinate affini, non potendo dividere per zero. Tali punti però possono essere messi in corrispondenza biunivoca con una retta proiettiva, come visto sopra.
Equazione della retta e punti della retta proiettiva .
Siamo partiti da un piano ed arrivati ad una retta, i cui punti coincidono con le direzioni delle rette del piano passanti per l'origine. Ma nel piano, con le coordinate abituali, qual'è l'equazione di una retta? Consideriamo rette per l'origine, quindi l'equazione sarà: ax+by=0. Chiaramente, se moltiplichiamo per un valore <> 0, l'equazione rimane sempre vera. Questa retta corrisponde ad un punto (direzione) di ; quale sarà? Semplicemente il punto di coordinate omogenee (b,-a). Facciamo ora uno sforzo in più e andiamo nel piano affine (quello solito, tanto per capirsi). L'equazione di una retta sarà ax+by+c=0; la sua direzione (o punto improprio) sarà il punto di coordinate omogenee (b,-a,0); consideriamo due retta parallele, ad esempio 2x+4y+3=0. 2x+4y+7=0
Il punto improprio (direzione ) di entrambe sarà (4,-2,0). Se guardiamo adesso alle rette come immerse nel piano proiettivo, le loro equazioni si trasformano passando da coordinate affini a coordinate omogenee:
x--->X/Z,y--->Y/Z; le equazioni (siamo nel piano affine , Z<>0) diventano:
2X/Z+4Y/Z+3=0
2X/Z+4Y/Z+7=0
2X+4Y+3Z=0
2X+4Y+7Z=0
notiamo che il punto (4,-2,0) appartiene ad entrambi le rette; basta infatti sostituire:
2*4-4*2+3*0=0
2*4-4*2+7*0=0;quindi appartiene all'intersezione delle due rette. Nel piano proiettivo, due rette parallele si incontrano in un punto improprio. Che due rette non parallele si incontrino sempre in un punto lo sappiamo già; quindi nel piano proiettivo due rette si incontrano sempre.
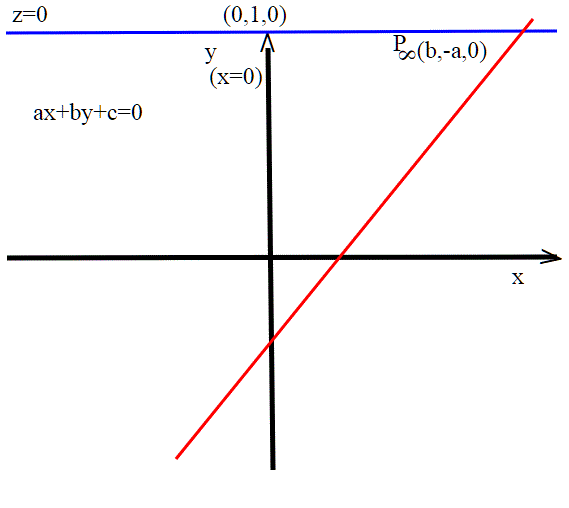
Che punto improprio ha l'asse y? Be', la sua equazione è x=1* x=0, quindi (b,-a,0)=(0,1,0) (sarebbe -1, ma moltiplichiamo per -1 ottenendo un punto equivalente).
Equazioni algebriche omogenee.
Una equazione algebrica è rappresentata da un polinomio in una o più variabili di cui si cercano le radici. Essa è determinata da una espressione del tipo F(x,y)=0 (se per esempio siamo in due variabili). Un equazione algebrica omogenea è un'equazione algebrica in più variabili i cui termini hanno tutti lo stesso grado. Facciamo un esempio:
è un equazione algebrica omogenea in due variabili. La particolarità delle equazioni omogenee è che ammettono sempre una soluzione banale, quella in cui le variabili sono tutte nulle. se prendiamo infatti la nostra equazione e sostituiamo a x,y i valori 0,0 otteniamo:
.
Notiamo una cosa; se una equazione omogenea ha una soluzione, allora ne ha infinite. Prendiamo sempre come esempio l 'equazione:
che ha come soluzione la coppia (1,1) allora preso un λ qualsiasi, λ(1,1)=(λ,λ),
Questo ci ricorda subito i discorsi fatti sulle coordinate omogenee; se studiamo quindi delle equazioni nel piano proiettivo, dobbiamo per forza trattare equazioni omogenee.
Equazione generica di una curva ellittica nel piano proiettivo
Abbiamo visto nell'introduzione che per studiare in modo completo una curva ellittica da punto di vista algebrico (legge gruppale) abbiamo bisogno dei punti all'infinito; quindi possiamo pensare di usare il piano proiettivo; ma nel piano proiettivo ci sono le coordinate omogenee, quindi anche la forma generale dell'equazione ellittica deve essere omogenea. Studiamo quindi le equazioni del tipo*:
1)
(nota *: l'equazione è stata semplificata usando trasformazioni un particolare sistema di coordinate ; ciò comunque nulla toglie alla validità del discorso)
qualcuno mi dirà; cos'è questa cosa così complicata? non assomiglia affatto all'equazione:
2)
ed ha una variabile in più, Z. Ma se ricordiamo il legame fra coordinate omogenee e coordinate affini, vediamo che infondo sono la stessa cosa. Infatti se siamo nel piano affine, un punto si individua con due coordinate, (x,y). Vediamo che la 2) altro non è che la 1) eseguendo un cambio di coordinate da proiettive a coordinate affini (o non omogenee).
Sappiamo infatti che nel caso il punto sia nel piano affine, la coordinata Z è diversa da zero; dividiamo allora la 1) per :
sappiamo che ; se sostituiamo otteniamo proprio la 2):
.
Però adesso che siamo nel piano proiettivo possiamo risolvere il problema del punto all'infinito; come fare per trovare i punti all'infinito della curva? Facile,basta intersecarla con la retta proiettiva, ovvero la retta all'infinito. Tale retta sappiamo che ha equazione Z=0
si tratta quindi di risolvere il sistema:
che dà come unica soluzione X=0. Quindi abbiamo Z=0 e X=0. Questo unico punto, che chiameremo ha quindi coordinate omogenee (0,X,0), con X<>0. Infatti sappiamo che (0,0,0) non appartiene al piano proiettivo. Possiamo dividere per X essendo X<>0, ottenendo
=(0,1,0).
Cosa rappresenta ? Sappiamo che il punto improprio (b,-a,0) è la direzione della retta ax+by+c=0. Quindi (b,-a,0)=(0,1,0) dà b=0; quindi ax=0, a<>0, x=0. Questa è la direzione delle rette parallelea all'asse delle y, come abbiamo visto anche sopra.
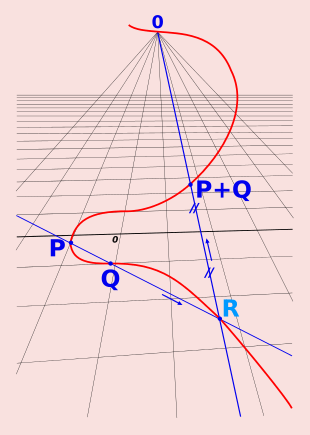
Quindi oltre ai punti affini soluzioni della 2) la curva ellittica ha anche un altro punto (improprio) che chiamiamo , o anche punto all'infinito. Siamo adesso in grado di dare una definizione più precisa di somma fra punti della curva:
Siano P;Q due punti appartenenti alla curva, e sia L la retta per P e Q. (Se P = Q,allora L è la retta tangente in P a E).
Sia R il terzo punto di intersezione di L con E e sia L' la retta passante per R e .
Allora L' interseca E in R; e in un terzo punto che denotiamo con P + Q. Questa nuova definizione di somma comprende anche quella data in precedenza, ed è valida sempre, anche la retta per P e Q dovesse essere parallela all'asse delle y. Ma questo,e anche la verifica che con questa operazione abbiamo creato un gruppo, lo vedremo in dettaglio la prossima volta.






12 commenti
La geometria proiettiva è uno strumento che apre nuovi orizzonti e nuovi modi di osservare e interpretare ciò che vediamo (e anche ciò che non vediamo). Le generalizzazioni che introduce consentono formulazioni e descrizioni di grande eleganza e sintesi.
Grazie, Umberto per aver portato all'attenzione questo argomento.
grazie a voi che vi prendete la pazienza di leggerlo. Spero possa servire a qualcosa.
Una osservazione a margine...
La figura di apertura di questo articolo rappresenta la curva di equazione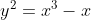 che era stata studiata nel quiz "Il fantasma di Galois".
che era stata studiata nel quiz "Il fantasma di Galois".
La figura in chiusura dell'articolo, davvero illuminante per capire l'andamento della curva all'infinito, ha equazione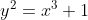
Ambedue sono comunque derivate dalla forma generale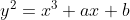 assegnando gli opportuni valori ai coefficienti "a" e "b".
assegnando gli opportuni valori ai coefficienti "a" e "b".
Il fatto che nel primo grafico la linea sia divisa in due parti, mentre nell'ultimo grafico la linea è unica, non ha alcuna rilevanza sulla loro comune natura di "curva ellittica" e sul modo in cui si rapportano con la retta impropria, intersecandola all'infinito.
non dico che è una osservazione pertinente perché direi una banalità. Se devo dirti la verità, chiaramente dipende dai coefficienti dell' equazione a b . Però non ho pensato ad una relazione fra di essi, e non so se ci sia. potrebbe essere un Quiz interessante: Che relazione deve esserci dara i tre coefficienti a b della curva affinché non sia un unico ramo?
Intuitivamente direi che per avere due rami il coefficiente di x deve essere negativo, ma certo va dimostrato per bene.
Non riesco scaricare il PDF
Ho un problema al mio computer o succede anche ad altri?
Claudio
no,hai ragione, non riesco a scaricarlo neppure io. Ho provveduto ad inoltrare la problematica all'amministratore del sito.
Il plugin che consente la conversione in pdf funziona, ma credo che in questo articolo ci sia qualche carattere che non viene riconosciuto, infatti non riesco neanche a copiarlo su word e lo stesso problema si verifica con la soluzione del quiz sulla torta virtuale. Tutti gli altri articoli si scaricano senza problemi.
Pensando che si trattasse di un problema di pesantezza del file dovuto alle molte figure, ho provato a copiarlo su word a pezzi, ma word si è piantato quando ho copiato la parte dedicata a retta e piano proiettivo: forse è qui che bisogna indagare per capire quale sia il problema (che non ho mai incontrato prima, nonostante abbia scaricato in pdf quasi tutti gli articoli del Circolo).
Lo scrivo pubblicamente, sperando che qualche lettore esperto possa avere già incontrato questa problematica e abbia qualche suggerimento in merito.
Grazie!
Noto che l'ultima figura deborda dalla pagina. Forse si potrebbe ripubblicare posizionandola più in alto.
ci avevo pensato anche io ma ero fuori sede. adesso funziona.
Grazie Maurizio il tuo intuito è sempre eccezionale.
Claudio puoi scaricare il pdf.
Ora funziona anche per la soluzione della torta virtuale (che non aveva nessuna figura "fuori bordo")... potenza del Bernardi: chissà cos'avrà combinato zitto zitto!
Un'avvertenza: sono riuscita a scaricare questo articolo al terzo tentativo, quindi a volte funziona a volte no, se qualcuno avesse difficoltà, può chiedere il file a papalscherzone@gmail.com che lo invierà per e-mail.