Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO nel quale è stato inserito anche il presente articolo

 

Da Fizeau a oggi i maggiori passi in avanti sono stati soprattutto di tipo tecnologico. Noi ci limitiamo a descrivere le più importanti variazioni sul tema, che ci portano fino ad oggi.

L’esperimento di Fizeau aveva molti punti critici di tipo soprattutto tecnologico, ma era geniale nella sua impostazione di base. Era soprattutto la ruota dentata a dare i maggiori problemi. Ne seguì che gli sforzi posteriori si basarono soprattutto sulla sostituzione della ruota dentata con strumentazione ottica più accurata. Ancora oggi è l’esperimento più usato per la determinazione della velocità della luce, utilizzando ovviamente quanto di più sofisticato ci sia in commercio.

Vale, quindi, la pena descrivere brevemente quanto fatto da Foucault l’anno dopo (1850), probabilmente in stretta collaborazione con lo stesso Fizeau. In particolare, il nuovo esperimento fu eseguito completamente in laboratorio, senza bisogno di avere grandi distanze a disposizione. Al posto della ruota dentata si inserì uno specchio rotante, capace di deflettere la luce di un angolo misurabile.

Innanzitutto, descriviamo uno dei punti fondamentali dell’apparato: il legame tra angolo di deflessione e angolo di rotazione dello specchio. Consideriamo la Fig. 3

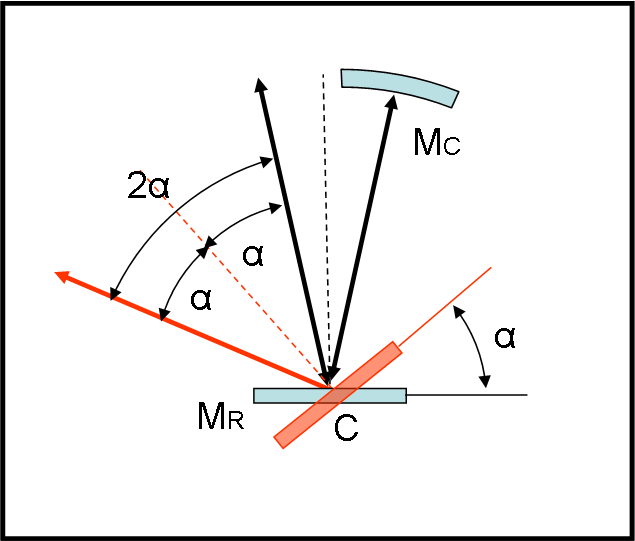
Per comodità sistemiamo lo specchio rotante M_R in posizione orizzontale. La luce proviene da S e viene riflessa mantenendo l’angolo di incidenza e va a colpire uno specchio M_C curvo, tale che il suo centro di curvatura sia proprio il punto C attorno a cui può ruotare M_R. Questa scelta comporta che tutti i raggi luminosi che vanno da C a un punto qualsiasi di M_C devono tornare indietro verso C per la stesso percorso.

Il raggio ritorna, quindi, in C. Lo specchio M_R non si è mosso e tutto è perfettamente uguale a ciò che è successo all’andata. Ragione per cui, il raggio di ritorno si riflette su M_R e torna verso S. Tutto questo percorso (di andata e ritorno) è segnato con le linee nere.

Il passo successivo ha l’inizio tale e quale: la luce parte da S, colpisce M_R in C e  si riflette raggiungendo M_C. Poi torna indietro per la stessa strada. Nel frattempo, però, lo specchio M_R è stato ruotato di un angolo α. Il raggio che proviene da M_C colpisce M_R in C, ma la riflessione deve avvenire simmetricamente rispetto all’asse dello specchio che è ora la linea tratteggiata rossa. Il raggio, perciò, torna indietro seguendo la linea rossa continua. Da considerazioni geometriche immediate, segue che l’angolo tra raggio di andata (nero) e raggio di ritorno (rosso) è esattamente uguale a 2α. Questa conclusione è di grande importanza dato che lo spostamento tra la sorgente e l’immagine finale è strettamente legata all’angolo 2α.

Guardiamo, allora, lo schema dell’intero apparato in Fig. 4.

 

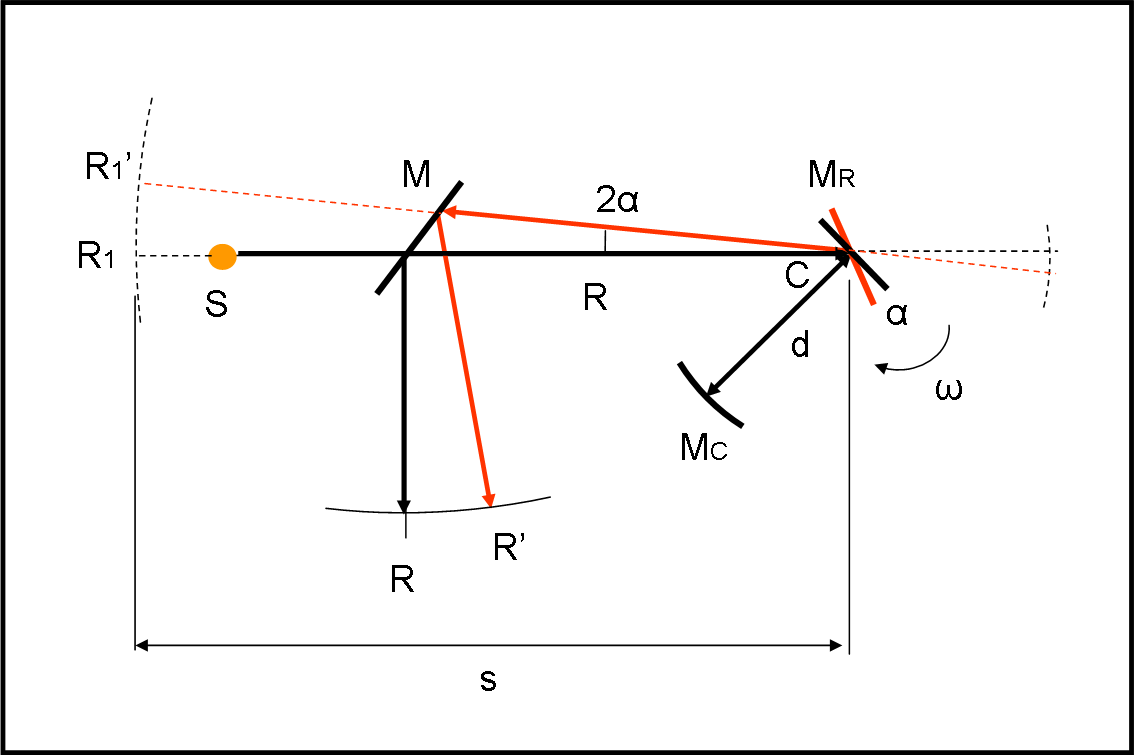
La sorgente S invia la luce che attraversa uno specchio M semiriflettente, in modo che una parte prosegua verso lo specchio rotante. L’andata è rappresentata dalla linea nera. Se lo specchio rotante è fermo, la luce torna indietro per lo stesso percorso e lo specchio M la invia verso la superficie di raccolta finemente graduata. Si ottiene la posizione R. Ripetiamo l’osservazione, ruotando però lo specchio M_R durante il “viaggio” M_R-M_C e ritorno. Lo specchio M_R è ruotato di α, mentre il raggio rosso che torna indietro è adesso ruotato di 2α rispetto a quello precedente. Esso va a colpire la superficie di raccolta in R’.

Sappiamo quanto vale la velocità angolare della rotazione dello specchio M_R:

ω = 2π/P

P è, ovviamente, il periodo di rotazione.

Ma vale anche:

ω = α/t

t = α/ω          …. (1)

Andiamo, adesso, a studiare da vicino cosa succede tra M_R e M_C. In un certo tempo t la luce deve andare da M_R e tornare dopo la riflessione. Si ha perciò che la velocità della luce  è data da:

c = 2d/t         …. (2)

Nello stesso tempo, però, sappiamo di quanto è ruotato lo specchio attraverso la (1). Sostituendola nella (2) si ha:

c = 2dω/α

d è noto e ω può essere cambiato dall’operatore. Ovviamente, essendo il tempo sempre lo stesso (dipende solo dalla distanza d e dalla velocità della luce) la (1) ci dice che per avere un angolo α misurabile deve anche essere molto elevata la ω.

Ma come facciamo a misurare l’angolo α? Niente di più facile! Guardando di quanto si sposta la posizione di R’ rispetto a R. Infatti, R e R’ possono essere ribaltati in R₁ e R₁’. Facendo centro in C si ottiene l’arco di cerchio R₁R₁’. Misurare RR’ è come misurare R₁R₁’ e conoscendo la distanza s si misura facilmente l’angolo 2α.

Questo fatto comporterebbe una deformazione circolare della superficie di osservazione. In realtà, l’angolo è molto piccolo e si può tranquillamente approssimare l’angolo con la sua tangente e quindi usare una superficie piana.

La strumentazione era decisamente più complicata, dovendo tener conto di lenti aggiuntive che dovevano focalizzare i fasci di luce. Il concetto, però, è quello illustrato precedentemente in modo semplificato.

Foucault ottenne un valore di c pari a 298 000 km/s, decisamente migliore di quella di Fizeau. Ricordiamo che quello  accettato oggi è pari a 299 792 km/s

Dopo Foucault, molti altri utilizzarono il suo metodo, cercando di migliorare le condizioni di misura e la strumentazione. Uno di questi fu proprio Michelson che provò svariate volte, sostituendo anche lo specchio rotante con uno specchio ottagonale e aumentando enormemente la distanza tra specchio rotante e specchio fisso (35 km): il primo sul Monte Wilson e il secondo sul monte Backly (Fig. 5). Egli ottenne il valore di  (299 796 +/- 4) km/s.

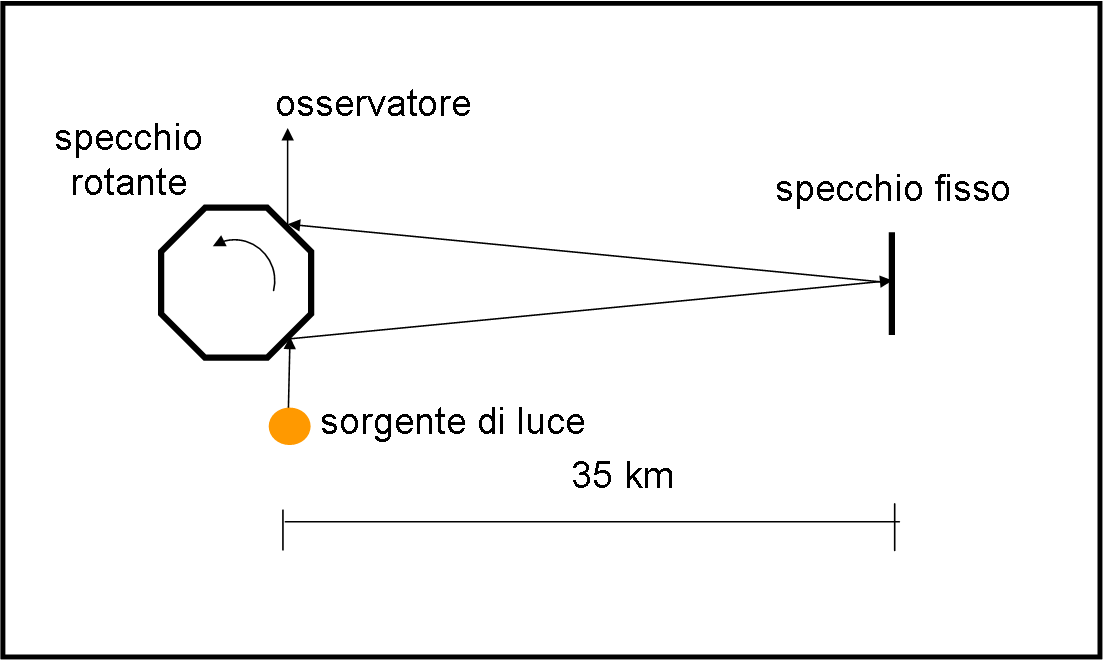
Lo schema è molto semplice e la velocità di rotazione è quella in grado di ottenere la situazione simmetrica della figura. Lascio a voi i facili calcoli necessari…

E’ interessante comprendere quanta accuratezza veniva messa nelle misurazioni e nelle apparecchiature. A titolo di esempio, riportiamo un articolo scritto dallo stesso Michelson mentre lavorava al Naval Observatory di Washington (circondato da un magnifico parco che pullula di simpaticissimi procioni lavoratori… non me ne sarei più andato…).

 

In attesa che siano riuniti in un unico approfondimento, QUI trovate tutti gli articoli dedicati alla misura della velocità della luce finora pubblicati