Soluzione Quiz: La " rivincita" di Achille

17/05/18

Soluzione Quiz: La " rivincita" di Achille

Categorie: Fisica classica Matematica Quiz Tags: Scritto da: Club dei Maghi Commenti:0

QUI il quiz di cui il presente articolo costituisce la soluzione

 

Achille ha fatto la scelta giusta, rinunciando a sfidare la Tartaruga per avere la rivincita , l'ipotesi di scendere lungo il piano inclinato nella speranza di impiegare meno tempo di quello della tartaruga, lungo la cicloide, era assolutamente da scartare. Di certo la Tartaruga avrebbe accettato, ridendo sotto i baffi (ma ce li hanno i baffi le tartarughe?). Comunque sia, Achy avrebbe fatto una pessima figura, come lui stesso ha capito facendo i suoi calcoli.

Eccoli qui.

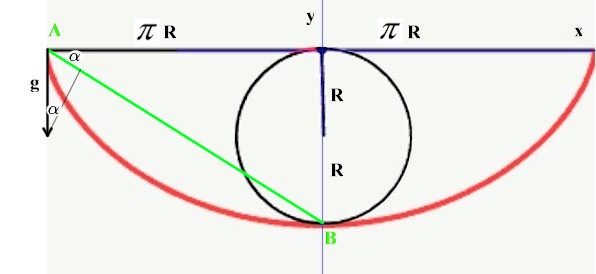
pianociclo

L'angolo del piano inclinato è facilmente calcolabile in base alle misure del dislivello e della proiezione orizzontale del tratto AB

\alpha =arctan(\frac{2R}{\pi R})  =   arctan(\frac{2}{\pi })

Esprimiamo ora l' accelerazione  che agisce sui corpi in movimento, non è altro che la componente della accelerazione di gravità nella direzione del moto lungo il piano inclinato.

a = g sen\alpha       possiamo scriverla come derivata seconda dello spazio

s"  =   \frac{d^2s}{dt^2}= gsen\alpha       integrando nel tempo otteniamo la velocità

s'  =  \int gsen\alpha dt=gsen\alpha * t + C     la costante C vale zero perché tale è la velocità iniziale

eseguendo una nuova integrazione otteniamo lo spazio

s=\int gsen\alpha *t dt = gsen\alpha * \frac{t^2}{2} + C   la costante C vale zero perché tale è lo spazio iniziale

Ora Achille fa questo ragionamento:  Se esprimo la distanza da A a B lungo il piano inclinato e la uguaglio alla espressione dello spazio che ho appena calcolato, in funzione del tempo, posso ricavare il tempo necessario a compiere la discesa, cioè il "mio" tempo.

AB  =\sqrt{(2R)^2+(\pi ^2R^2)}  =R\sqrt{4+\pi ^2}     = gsen\alpha *\frac{t^2}{2}

da cui    t^2= \frac{2R\sqrt{4+\pi ^2}}{gsen\alpha }       ricavando quindi    t   ed esplicitando l'angolo \alpha

t = \sqrt{\frac{2R\sqrt{4+\pi ^2}}{gsen( arctan\frac{2}{\pi })}}     che chiameremo  T_a  per indicare che questo è il tempo di Achille

Questo tempo va confrontato con quello della tartaruga, T_t  che è un quarto del tempo segnato dai due concorrenti il giorno precedente. Come ha subito intuito Achille, vale un quarto del periodo di oscillazione sulla cicloide.

T_t = \frac{1}{4}*2\pi \sqrt{\frac{4R}{g}} = \sqrt{\frac{\pi ^2R}{g}}

Non resta che confrontare i due tempi mettendoli in rapporto

 

\frac{T_a}{T_t}=\sqrt{\frac{2R\sqrt{4+\pi ^2}}{g sen( arctan\frac{2}{\pi })}}   * \sqrt{\frac{g}{\pi ^2R}}=    \sqrt\frac{2\sqrt{4+\pi ^2}}{\pi ^2 sen(arctan\frac{2}{\pi })}        \simeq\frac{2,72}{2,30}

In quest'ultima espressione non appare l'accelerazione  di gravità g. Questo significa che anche gareggiando su un qualsiasi pianeta, diverso dalla Terra, non cambierebbe nulla. (Questa considerazione, inserita nella soluzione ben prima di pubblicare il quiz, coincide perfettamente con quanto ha scritto anche Andy nel suo commento)

Valutando il rapporto si ricava facilmente che T_a > T_t , quindi Achille ha fatto bene a rinunciare alla gara, sarebbe stato un vero smacco, lo potete vedere molto chiaramente grazie a questa bella animazione preparata da Mago Arturo.

https://ggbm.at/wPDH8wWf

Anche questa animazione , presente in un commento del solito Andy, è interessante in quanto mette a confronto i diversi tempi di percorrenza  fino al traguardo , di punti che si muovono su curve diverse, tra cui la linea inclinata e la cicloide. https://imgur.com/qTs2tkz

Una generalizzazione dalla impostazione risolutiva, proposta da Umberto commentando il quiz, fornisce un significativo valore aggiunto  per il fatto che può essere utilizzata per analizzare qualsiasi profilo. Eccovela:

___________________   (dal commento di Umberto )

Quello che volevo far notare nel precedente commento, è che è possibile una soluzione alternativa , e generalizzante.

Sappiamo infatti dal calcolo differenziale, che l'elemento infinitesimo di lunghezza di una curva in una variabile, y(x),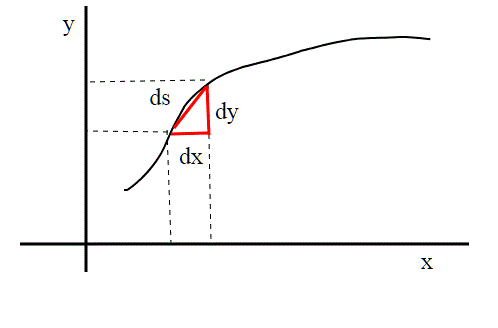lunghezzaCURVAil ds, si può ricavare da:

ds^{2}=dx^{2}+dy^{2}=dx^{2}+dx^{2}\cdot y'^{2} ove y^{'} è la derivata di y(x)

raccogliendo si ottiene ds^{2}=(1+y^{'2})dx^{2}.

per l'uguaglianza fra energia potenziale e cinetica, la velocità istantanea è data invece da:

v=\sqrt{2gy(x))} (vo iniziale =0)

ma allora il tempo infinitesimo, dt, è dato dal rapporto ds/v, ovvero  dt=\frac{\sqrt{(1+y^{'2})}}{\sqrt{2gy}}\cdot dx

il tempo totale, qualsiasi sia y(x), sarà allora

T=\int_{A}^{B}dt=\int_{A}^{B}\frac{\sqrt{(1+y^{'2})}}{\sqrt{2gy}}\cdot dx 1)

curvaintegrale

Nel nostro caso, ovvero con i dati del quiz,

T=\int_{0}^{\pi\cdot R }dt=\int_{0}^{\pi\cdot R }\frac{\sqrt{(1+y^{'2})}}{\sqrt{2gy}}\cdot dx

sempre nel caso che la velocità iniziale sia V0=0.

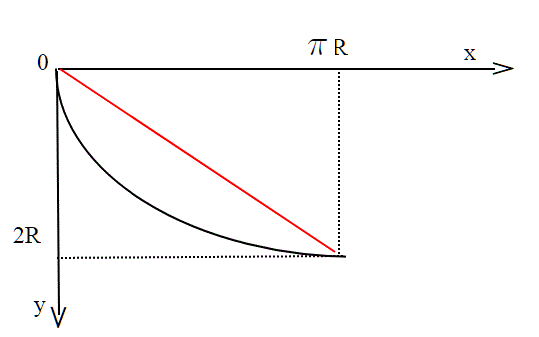
cicloide

Sempre nel caso particolare del quiz, y=\frac{2}{\pi } \cdot x, che è la retta del piano inclinato.

y^{'}(x)=\frac{2}{\pi }

e l'integrale diventa:

T=\int_{0}^{\pi\cdot R }dt=\int_{0}^{\pi\cdot R }\frac{\sqrt{(1+4/\pi ^{2})}}{\sqrt{2g\cdot \frac{2}{\pi }\cdot x}}\cdot dx

T=\frac{\sqrt{\pi }}{2\sqrt{g}}\frac{\sqrt{\pi ^{2}+4}}{\pi }\int_{0}^{\pi\cdot R }\frac{1}{\sqrt{x}}dx

l'integrale indefinito viene:

\frac{\sqrt{\pi }}{2\sqrt{g}}\frac{\sqrt{\pi ^{2}+4}}{\pi }\cdot 2\sqrt{x}

e calcolato l'integrale definito fra [0,\piR]

T=\frac{\sqrt{\pi }}{2\sqrt{g}}\frac{\sqrt{\pi ^{2}+4}}{\pi }\cdot 2\sqrt{\pi R}

e svolgendo i calcoli:

T=\sqrt{\pi ^{2}+4}\cdot \sqrt{ \frac{R}{g}}>\sqrt{ \frac{R}{g}}

Di sicuro questo non è il metodo più naturale nel caso del piano inclinato, ma l'ho introdotto per generalizzare il discorso; esso si può applicare per trovare il tempo di arrivo indipendentemente dalla curva, cioè y=f(x) può essere una qualsiasi  curva  che unisce i due punti. Di sicuro l'integrale 1) non sempre è facilmente risolvibile come in questo caso. Bisognerebbe provare con la parabola e il cerchio.

Per risolvere ancora in modo più generico il problema, bisognerebbe cercare la  funzione che rende minimo l'integrale 1). E qui potremmo applicare quello che tanto ha fatto faticare Fabrizio, ovvero le equazioni di Eulero-Lagrange, che ci  porterebbero ad una equazione in cui l'incognita è una curva  (equazione differenziale).Io non mi cimento, ma qualcuno lo farà. In tal caso scopriremmo proprio,come è noto dalla letteratura matematica,  che tale curva è proprio una cicloide.

__________________   Fine del commento di Umberto

Resterebbe un'ultima cosa da aggiungere...

Ricorderete che si era parlato, con Andy, di una curiosa variante al problema, consistente nell'introdurre nelle ipotesi una variabilità del campo gravitazionale.  Sappiamo che in effetti il campo gravitazionale, che per altitudini di misura trascurabile se confrontate con il raggio della terra si considera costante, varia con una legge che in prima approssimazione ha la forma   g(h)= g*(1-2h/R)   ove R è appunto il raggio terrestre e y esprime la quota del punto considerato.  Naturalmente dato che il raggio terrestre è di 6370 Km  l'influenza di questa variazione della accelerazione di gravità è normalmente del tutto trascurabile. Ma la domanda che ci si poneva era questa. Se  Achille e la Tartaruga scendessero lungo la stessa pista, la tartaruga dal punto più alto e Achille in prossimità del traguardo, nell'ipotesi che l'accelerazione sia variabile con la quota, aumentando via via che si va verso il traguardo, che differenza comporterebbe sul risultato della gara? Ricordo a tutti che, con g costante, entrambi giungevano all'arrivo contemporaneamente.

La risposta inoppugnabile la si ottiene ovviamente con gli strumenti matematici ma, lasciandoli da parte almeno per il momento  e non  volendoci affidare solo a "ragionamenti intuitivi" e sensazioni, una possibile alternativa è quella di costruire un rudimentale modello per simulare il sistema.

Partendo dal profilo di una cicloide sceglieremo una ventina di punti che consentano di approssimarne il profilo con una spezzata poligonale. Tareremo il massimo dislivello con un valore a nostra scelta e assegneremo tutte le coordinate in modo proporzionale a tale valore.

Ciascun segmento della poligonale è un tratto di piano inclinato a cui si associano tutti i parametri geometrici  di coordinate e conseguente pendenza.

Per quanto riguarda il valore della accelerazione di gravità teniamo valido, per ora il valore costante di 9,81 m/sec2

Nelle varie colonne riporteremo i termini che porteranno , applicando le equazioni del moto in questo sistema, alla velocità finale di ciascun tratto e al tempo di percorrenza parziale. Naturalmente la componente di velocità finale (orientata come la pendenza del nuovo tratto) sarà la velocità iniziale con cui lo affrontiamo. Alla fine potremo così conoscere il tempo totale e la velocità con cui ciascuno concorrente taglia il traguardo. Potremo fare una semplice verifica della rispondenza della simulazione confrontando il tempo ottenuto con  1/4 del periodo di oscillazione calcolato per la cicloide.      Se abbiamo fatto tutto per bene dovremmo avere un errore dell' 1 o 2 %.

Confrontiamo allora i tempi dei due concorrenti, che dovrebbero essere molto vicini tra loro.

Non resta ora che agire sul valore di g.  Teniamo conto che se usassimo nella formula g= 9,81 (1-ay)  il valore del raggio terrestre , non avremmo praticamente nessuna differenza: la g sarebbe ancora costante. Quindi, per esaltare il fenomeno, useremo un valore di a "enorme", diciamo 0,005. Sostituita alla g costante la g variabile, rieseguiremo le simulazioni e potremo constatare cosa succede. I due concorrenti arriveranno ancora insieme? La cicloide sarà, anche in questa situazione, abbastanza "tautocrona"?

 

QUI tutti i quiz dei Maghi

QUI tutti i quiz del blog

Vi è piaciuto calcolare questo percorso? QUI ne troverete altri!

Articoli correlati

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.