Eccoci davanti a due tipici non-quiz. Questo non significa che  i solutori abituali dei quiz (sono sempre i soliti noti) debbano sentirsi espropriati del  divertimento di provare a risolvere il problema. Possono benissimo riportare le loro soluzioni nei commenti. Proprio per il piacere che trovano a risolvere i quiz (ed è un grande merito) sicuramente non andranno a sbirciare le soluzioni ufficiali. Ormai li conosciamo troppo bene!

 

STRANEZZE SFERICHE

(a cura di Maurizio Bernardi)

Solo qualche settimana fa, questo avrebbe potuto essere un quiz, magari uno di quei quiz vanamente perversi di Nobody ai fratelli Pippo-Pappo-Peppa.

Invece ne faremo una semplice, inoffensiva esercitazione, molto più rilassante.

E' un problema interessante perchè sembra che manchi qualcosa, tra i dati forniti, per poter arrivare a formulare la soluzione. Ma non si tratta di ragionare nello stile io so che tu sai che io so... come altre volte si è fatto (vedi ad esempio il quiz degli isolani con gli occhi di vari colori, o quell'altro di Pippo e Pappo indaffarati a immaginare quante palline avrà l'altro fratello).

Questa volta la logica che può guidarci verso la soluzione è intrinseca al problema stesso.

Ma veniamo al sodo:

Immaginate una sfera solida, di metallo. Ora con una punta da trapano praticate un foro che l'attraversa da parte a parte, passando per il centro. Avete asportato nell'ordine: una calotta sferica in entrata, un nucleo cilindrico sottostante e, infine, una calotta sferica in uscita. L'altezza del nucleo cilindrico risulta essere esattamente di 6 cm

Qual è il volume residuo della sfera dopo l'operazione di trapanatura?

A prima vista sembra proprio che manchi qualche dato, vero? Per esempio il volume della sfera intera o, almeno, il suo raggio. Come si fa a trovare il residuo di una cosa di cui non si sa nulla?

 

E il foro? Che diametro avrà il cilindro? Sappiamo solo che l'altezza è di 6 centimetri, ma non ci vien detto nulla della base. In più, non è affatto semplice capire come calcolare il volume delle due calotte sferiche che verranno asportate, assieme al cilindro, da una parte e dall'altra, facendo il buco.

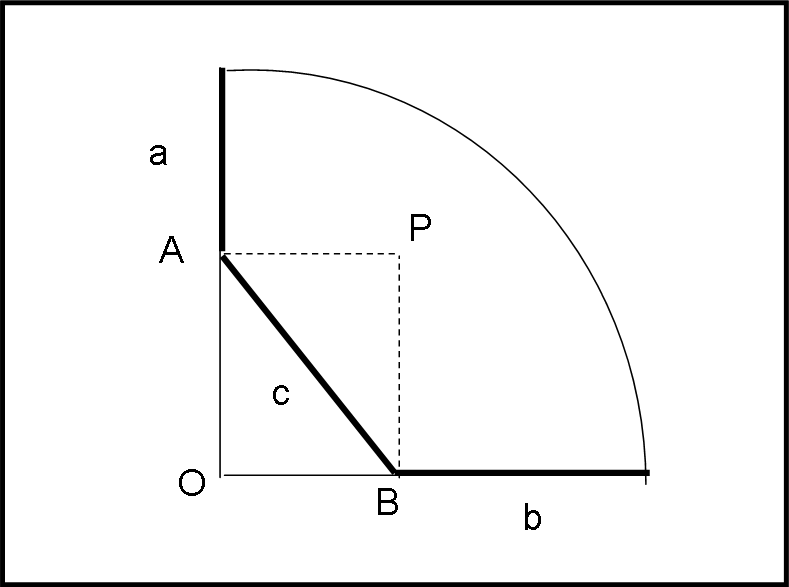
Come? Volete anche il disegno? Va bene, eccolo qui...

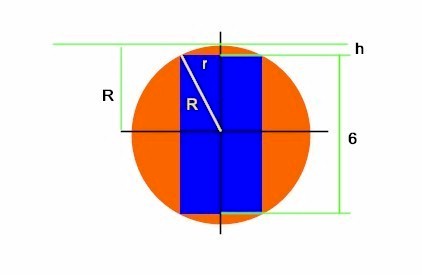
E ora, visto che la figura me l'avete fatta disegnare, proviamo a ragionarci sopra.

La cosa certa è che, avendo indicato con R il raggio della sfera, posso dire subito, grazie a Pitagora, che il raggio del cilindro sarà r = √(R² - 3²) e l'altezza di ciascuna delle due calotte sferiche alle sue estremità, che se ne andranno via col cilindro, varrà h = (R-3).

Ottimo! Per determinare il volume residuo della sfera, dopo la perforazione, cominciamo ad aggiungere al volume del cilindro il volume delle due calotte, poi sottraiamo il totale dal volume della sfera ed il gioco è fatto.

Allora, il volume del cilindro non è un problema: area base per altezza e vai. La cosa più complicata è calcolare il volume di una calotta che si può trovare, senza ricorrere agli integrali, con una semplice formula di geometria solida, che è la seguente Vcal= π h(3r²+ h²)/6. Esistono anche altre formule equivalenti, che funzionano altrettanto bene.

Ricordiamoci che r è il raggio di base del cilindro e quindi anche della calotta e che h è proprio la sua altezza. Facciamo questo calcolo e ci togliamo il pensiero.

Vresiduo = Vsfera – Vcil – 2Vcal

Vresiduo = 4/3 π R³ - 6 π(R²-3²) - 2 π h(3r²+ h²)/6

sostituiamo ad r e h i rispettivi valori,

Vresiduo = 4/3 π R³ - 6 π R² + 54 π - π (R-3)(R² - 3²) - π (R-3)³/3 sviluppiamo e semplifichiamo,

V residuo = 4/3 π R³ - 6 π R² + 54 π - π (R³-9R - 3R² +27) - π (R³-9R²+27R-27)/3

V residuo = 4/3 π R³ - 6 π R² + 54 π - π (R³-9R - 3R² +27) - π (R³-9R²+27R-27)/3 ordiniamo,

Vresiduo = π R³(4/3-1-1/3) + π R²(-6+3+9/3) + π R(9-27/3) + π(54-27+27/3)

Vresiduo = π 36

Fantastico, vero? Una bella sfacchinata ma, alla fine, un risultato pulito che ci dice che, qualunque sia la sfera, asportandone un torsolo centrale cilindrico di 6 cm di lunghezza (con le modalità descritte all'inizio del non-quiz), si ha sempre un volume residuo di π 36 cm³ , e si sarebbe tentati di dire che quel 36 è pure il quadrato di 6, ma lasciamo andare...

Però... ci potrebbe essere un ragionamento logico più sottile che ci eviterebbe tutto questo calcolo di volumi e relativa manipolazione di espressioni algebriche. Non riuscite ad intravederlo?

Ok, Ok... niente quiz, d'accordo (però se volete sospendere la lettura e provare a rispondere, ci fate piacere!).

Allora, ragioniamo come il signor John W. Campbell figlio, editore della mitica “Astounding Science Fiction”. Ecco come affrontò la questione:

“Il problema non sarebbe stato posto se non fosse possibile risolverlo. Quindi deve avere una soluzione indipendente dai dati “mancanti” che non sono essenziali. Ne consegue che il volume deve avere un valore unico, costante". (E questo è un bel salto in avanti).

Allora, anche se il buco si riduce a niente, un foro cilindrico lungo 6 cm, ma di area di base uguale a zero, anche in quel caso, il risultato è quello che cerchiamo.

Insomma, il volume residuo è proprio il volume di una sfera bucata solo virtualmente da un cilindro a spillo di lunghezza 6 cm che poi diventa anche il diametro della sfera, perchè le due calotte spariscono nel nulla. Ma quanto vale mai il volume di questa sfera residuale, in realtà intatta?

Facile, vale 4/3 π R³ con R=3, ossia 4/3 π 3³ = π 36

Questo sì che è fantastico.

Niente formule (giusto il volume della sfera), niente calcoli (solo 4 x 27/3) e il risultato è lì.

Se volessimo trarre una morale da questo non-quiz potremmo dire che, prima di lanciarci nella soluzione, meglio pensarci su un po'. Soprattutto se ci sembra di non avere tutti i dati necessari, come nel caso che abbiamo visto.

 

 

IL RAGGIO DI FEYNMAN

(a cura di Vincenzo Zappalà)

State calmi, non è  una roba di astrofisica, tipo il raggio della sfera di Hubble o il raggio di Schwarzschild. E' solo un innocuo raggio di un cerchio, che va trovato in base a tre dati noti. Richard Feynman c'entra solo perché alcune persone, invidiose e malevole, sostengono che, davanti al problema, il fisico più amato da generazioni di studenti, si sia messo a fare calcoli del tutto superflui.

Ma capirete meglio  se vi illustro il problema con questo semplice disegno:

 

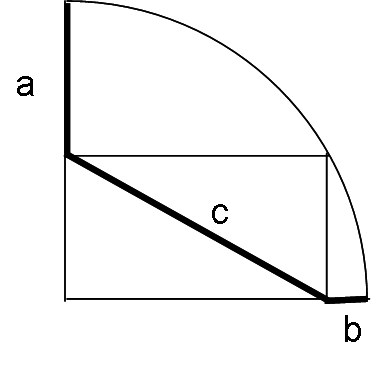
Ecco un quarto di cerchio e alcune misure a, b, c  indicate in figura.

Come possiamo calcolare il raggio?

Se non volete rispondere ne avete il diritto: anche se "la vita è tutta un quiz ..."  abbiamo detto e ridetto che questo è un non-quiz (ma se proverete a rispondere prima di continuare a leggere, ci farete felici!).

 

Non crediamo che Feynman abbia veramente usato questo metodo... ma tutto è possibile.

Basta scrivere la semplice relazione tra a, b e c, nella quale appare il raggio incognito R, e ricavarlo.  Con Pitagora, posso scrivere

adesso ordiniamo tutto al membro di destra, per potenze decrescenti di R:

applichiamo la formula risolutiva ridotta per le equazioni di secondo grado.

Ed ecco qua il raggio R, in funzione di a , di b  e di   c

 

La soluzione è trovata... ma il problema è di ben più facile soluzione!

Basta guardare questa animazione:

 

Fin dall'inizio, osservando con attenzione  la figura si può notare che c  non è altro che  una delle due diagonali del rettangolo. L'altra diagonale, certamente di lunghezza pari a c, è proprio il raggio R.

La morale della favola ve la facciamo dire da Richard...

 

 

Intuito, colpo d'occhio e un pizzico di fantasia possono aiutare a risolvere un problema e/o a trovare una soluzione semplice ed elegante, ma, in matematica, le soluzioni "occhiometriche" devono essere supportate da una rigorosa dimostrazione formale e di carattere generale.

Analizziamo, pertanto, il caso generale in cui a e b siano scelti a caso, con c che ne viene di conseguenza. In questo caso l'equazione precedente con a, b e c è obbligatoria. 

La figura è quella che segue:

 

Senza mostrare il rettangolo  OAPB la soluzione si trovrerebbe lo stesso. Tuttavia, si può far scorrere la retta  x = R - b fino ad arrivare al caso particolare considerato prima (il punto intersezione delle due rette y = R -a  e  x = R - b" sta proprio sulla circonferenza!), come mostra la figura seguente

Applicare la formula, in questo caso sarebbe inutile, come già abbiano visto...

Ammettiamo di non avere righelli (ma se anche l'avessimo saremmo proprio sicuri di tracciare bene le linee?), qual è la verifica da fare prima di partire con la solita equazione?

Basta calcolare 

(c" -a)² + (c" - b")²

Se questa relazione vale c"², allora possiamo subito dire che R = c", senza risolvere l'equazione precedente.

Il fatto di avere usato l'equazione per vari valori di a, di b e di c in modo obbligatorio, potrebbe  istigare a farlo anche nel caso particolare in cui  la diagonale è proprio uguale al raggio.

Basta, quindi, effettuare una piccola verifica preventiva (senza usare la riga...). 

Forse Feynman è caduto in questa svista a causa della ripetizione di un calcolo sempre uguale e obbligatorio? Mah... noi crediamo proprio di no... però, conoscendo il suo senso dello "humor", avrebbe potuto proporre il problema a qualche suo allievo...

 

Gli autori ringraziano la solita Daniela che ha sudato quattro camicie per mettere in bella copia e con la necessaria logica le farneticazioni dei due amici galattici...

 

Se vi è piaciuto questo NON-QUIZ, ne trovate altri QUI