Un problema esponenziale ***/****(Integrato con altra soluzione )

20/08/18

Un problema esponenziale ***/****(Integrato con altra soluzione )

Categorie: Matematica Tags: Scritto da: Umberto Cibien Commenti:4

Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Ricordate le funzioni esponenziali? Io ne  ho trattato la definizione in   questo  articolo, ma nell'archivio potete trovare vari articoli che ne parlano, a partire da qui. Vogliamo approfondire l'importanza di tali funzioni discutendo il seguente problema, abbastanza noto . Io propongo la mia soluzione, chi ne troverà altre alternative potrà aggiungerle ai commenti. La mia soluzione è personale e un po' artigianale.. ma scende a basso livello per una comprensione maggiore. Chi non vuole poi affatto leggere la soluzione può darne  una propria.

 

Il Problema

Un oste un po' disonesto e anche molto distratto, decide di annacquare il vino di una botte. Prende una botte di 100 litri, la riempe per metà di vino (50 litri) e poi tramite una canna di gomma collegata ad un rubinetto d'acqua, decide di completare il riempimento con 50 litri d'acqua. Il flusso d'acqua generato dal rubinetto è di 5 l/m (litri al minuto).

Senza-titolo-1

Cosicché dopo 10 minuti la botte è piena, ma l'oste si è però completamente dimenticato di aver cominciato il riempimento, per cui la miscela di acqua-vino comincia a straripare. Solo dopo un ora l'oste si accorge e chiude il rubinetto dell'acqua, ma ormai il danno è fatto; molto vino è uscito con la miscela vino-acqua. La domanda è:

quanto vino rimane nella botte dopo quella fatidica  ora?

Premessa

La nostra incognita in funzione del tempo è la concentrazione del vino nella miscela, che consideriamo omogenea ad ogni instante. Se chiamiamo Qv la quantità di vino presente nella botte, la concentrazione di vino sarà:

C=Qv/100 essendo 100 l il volume totale della botte.

Chiaramente la miscela varia ad ogni istante, in quanto diminuisce in funzione del suo stesso valore. Infatti, chiamando F=5 l/m il flusso entrante di acqua nella botte, esso crea un flusso uscente di miscela.  Il volume della miscela uscente è proporzionale al flusso F e al tempo in cui viene considerato.   Il volume del vino uscente è proporzionale alla concentrazione C di vino nella miscela uscente. Quindi la concentrazione del vino varia in proporzione al valore della concentrazione stessa. Questo è un tipico problema esponenziale; sappiamo già che le funzioni esponenziali variano nel tempo in funzione della loro grandezza. Il problema andrebbe risolto immediatamente con una equazione differenziale, ma non tutti , a mio avviso, possono capirne l'impostazione immediatamente. Per cui procediamo in altro modo e per gradi.

(Per chi vuole trovare una soluzione autonoma, l'articolo termina qui).

Soluzione: una prima approssimazione.

Il tempo gioca un ruolo essenziale nella soluzione di questo problema. Sappiamo che nella realtà  esso scorre in modo continuo, quindi ad ogni istante la concentrazione di vino cambierà il suo valore.

Noi cominciamo però a considerare il tempo in modo discreto, facendolo scorrere allo scatto dei minuti.

 

0 1 2 3 4 .. .. .. 60 minuti

 

Chiamiamo C0, C1,....Cn la concentrazione all'n-esimo minuto.

C0( concentrazione al minuto zero):

C0=50/100 (50 litri di vin0)

Per far variare il tempo in modo discreto, ipotizziamo che solo allo scadere del primo minuto si abbia la fuoriuscita del volume V1=F*1=5 l. Come viene a variare la concentrazione? Dobbiamo calcolare la quantità di vino che resta nella botte,

Qv1= 100*C0-C0*5=C0*95

Quindi C1=Qv1/100=C0*95/100=47,5/100=0,475.

Passiamo allora a t=2 minuti. Calcoliamo Qv2, C2

Qv2=100*C1-C1*5=C1*95

C2=C1*95/100=0,475*0,95=0,45125

ci accorgiamo adesso che possiamo sostituire a C1 l'espressione con C0

 

C_{2}=C_{1}\frac{95}{100}=C_{0}\cdot \frac{95}{100}\cdot \frac{95}{100}=C_{0}(\frac{95}{100})^{2}=0,45125

Poniamo  k=95/100;

C_{2}=C_{0}k^{2}

e C3? basta moltiplicare C2 per k:

C_{3}=C_{2}k=C_{0}k^{2}k=C_{0}k^{3}.

E per n qualsiasi?

C_{n}=\frac{C_{n-1}\cdot 100-5\cdot C_{n-1}}{100}=k\cdot C_{n-1} Cioè per calcolare la concentrazione successiva basta moltiplicare quella attuale per k.

Quindi:

C_{n}=C_{0}k^{n}

che rappresenta proprio un andamento esponenziale decrescente, essendo k<1. Tutto questo si può dimostrare formalmente per induzione.

Infatti per n=0, C_{0}=C_{0}\cdot k^{0}=C_{0}\cdot 1=C_{0}

supposto  C_{n-1}=C_{0}k^{n-1} ed essendo  C_{n}=\frac{C_{n-1}\cdot 100-5\cdot C_{n-1}}{100}=k\cdot C_{n-1} come visto sopra,  concludiamo cheC_{n}=C_{n-1}\cdot k=C_{0}k^{n-1}\cdot k=C_{0}k^{n}

 

Quindi senza fare tanti calcoli,possiamo ricavare che la concentrazione allo scadere del 60° minuto è:

C_{60}=C_{0}k^{60}\simeq0,02303489

pari ad un vino residuo uguale a 0,02303489*100= 2,303489.

Questo non è il risultato esatto, ma è una prima approssimazione. Non abbiamo tenuto conto della continuità di uscita del vino e quindi della variazione continua della concentrazione.

Affiniamo la soluzione

Che calcoli abbiamo fatto fino adesso? Abbiamo considerato il valore costante per la concentrazione, nell'intervallo di tempo unitario. Qui l'unità di misura usata è il minuto. E se facessimo gli stessi calcoli ogni secondo? Di sicuro otterremmo un valore più preciso. Il flusso F=5 l/m viene espresso in l/s dividendo 5 per 60:

F=5/60=0,0833333333.. Per calcolare il nuovo K dobbiamo sostituire:

k=(100-0,083333333)/100=99,916666666666/100

nella formula \dpi{120} C_{n}=C_{0}k^{n} dobbiamo adesso  inserire il tempo finale  in secondi, ovvero 3600 s. *

Otteniamo:

C_{3600}=\frac{1}{2}(99,916666666666/100)^{3600}=0,024856

Mentre il vino rimanente risulta 0,024856*100= 2,4856. Vedremo tra poco che questo valore si avvicina di molto al valore esatto.

  • * NB: Si tende a confondere il tempo finale con gli intervalli in cui è diviso tale tempo. L'esponente di k non è il tempo finale, ma il numero di suddivisioni.

Calcoliamo il valore esatto con un passaggio al limite.

Siamo passati dal minuto al secondo per applicare il nostro procedimento; cosa ci vieta di diminuire fino a zero l'intervallo in cui calcoliamo il volume uscito e quindi la concentrazione? Nessuno chiaramente, basta fare un passaggio al limite.

Ricordiamo però prima il limite fondamentale che definisce e, numero di Nepero:

\lim_{n \to \infty}(1+\frac{1}{n})^{n}=e

e una leggera manipolazione di questo limite, che ci dà un altro limite importante:

\lim_{n \to \infty}(1+\frac{1}{an})^{an}=e   1)

Infatti se poniamo y=na, anche y tende ad infinito e il limite diventa sostituendo:\lim_{y \to \infty}(1+\frac{1}{y})^{y}=e

Supponiamo di dividere l'intervallo di 60 minuti per N intervalli di tempo. Calcoliamo il valore di k. In questo caso, l'intervallino di tempo sarà uguale a L(In)=60/N, dove con L si indica la durata . Il valore corrispondente di k sarà allora:

k=(1-\frac{F}{V}\cdot \frac{60}{N})

infatti, k è il numero che ci fa passare da Cn a Cn+1:

C_{n+1}=\frac{C_{n}\cdot V-\frac{F\cdot 60\cdot C_{n}}{N}}{V}=C_{n}\cdot \frac{ V-\frac{F\cdot 60}{N}}{V}

C_{N}=C_{0}k^{N}=C_{0}(1-\frac{F}{V}\cdot \frac{60}{N})^{N}

poniamo ora a=-\frac{V}{60F} e riscriviamo l'espressione sopra:

C_{N}=C_{0}(1+\frac{1}{aN})^{N}

e elevando ad a e a 1/a:

C_{N}=C_{0}((1+\frac{1}{aN})^{aN})^{\frac{1}{a}}

adesso facciamo tendere il numero di suddivisioni ad infinito; In tenderà a zero. Usiamo ora il limite fondamentale 1)

\dpi{120} \lim_{N \to \infty}C_{N}=C_{0}((1+\frac{1}{aN})^{aN})^{\frac{1}{a}}=C_{0}e^{\frac{1}{a}}

Sostituiamo adesso ad a il suo valore ottenendo:

\dpi{120} \dpi{120} \lim_{N \to \infty}C_{N}=C_{0}e^{-\frac{60F}{V}}=\frac{C_{0}}{e^{3}}=\frac{1}{2\cdot e^{3}}=0,024893584

quindi la quantità di vino esatta  rimasta nella botte (il cui volume è sempre 100 litri) è

Qv=2,4893.

Abbiamo risolto il problema per t=60. E per t generico? Basta sostituire t al posto di 60. Otteniamo:

\dpi{120} C(t)=C_{0}e^{-\frac{t\cdot F}{V}}

Torneremo ancora su questa formula, dimostrandola anche in altro modo. Essa rappresenta la funzione di decadimento esponenziale, molto utile in fisica.

L'equazione differenziale

Visto che Maurizio ha trovato una soluzione alternativa usando le equazioni differenziali, vorrei integrare tale soluzione nell'articolo, cercando assieme una spiegazione semplice, che tutti possano comprendere. Questa spiegazione nasce da una collaborazione fra me e Maurizio, svolta in privato.

La spiegazione si basa sul concetto di limite e derivata. Vorrei partire un po' da lontano, dal concetto di velocità.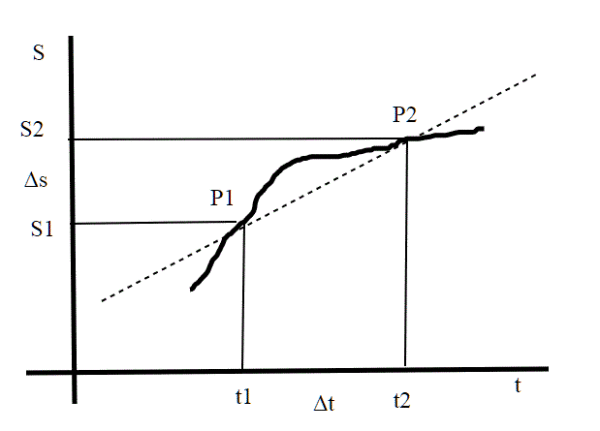p1

Se un punto si muove di moto uniforme, facciamo presto a calcolare la sua velocità istantanea facendo direttamente il rapporto  fra spazio percorso e tempo impiegato, qualsiasi siano i tempi e gli spazi corrispondenti:

\dpi{120} \dpi{120} v=\frac{S}{T}. Ma in generale,se il moto di un punto non è uniforme e la sua legge oraria non è una retta, e tale rapporto non è costante  dipende dagli intervalli considerati. Tale velocità, non potendo essere calcolata puntualmente non essendo uniforme, sarà una  velocità media:

\dpi{120} \dpi{120} v_{m}{}(t_{1},t_{2})=\frac{S_{2}-S_{1}}{t_{2}-t_{1}}=\frac{\Delta S}{\Delta t}

se vogliamo conoscere la velocità punto per punto, dobbiamo affidarci ai limiti. In pratica dobbiamo far tendere \dpi{120} \Delta t \rightarrow 0, ottenendo la derivata nel punto voluto.

\dpi{120} \dpi{120} \dpi{120} \dpi{120} v=\lim_{\Delta t\rightarrow 0}\frac{\Delta S}{\Delta t}=\frac{ds}{dt}=S'(t); tale derivata sappiamo poi che corrisponde graficamente alla retta tangente al grafico nel punto considerato.

Perchè ho fatto questo discorso sulla velocità? Perchè per impostare l'equazione differenziale dobbiamo ragionare sulla velocità di variazione della concentrazione del vino nella botte.

Indichiamo come di consueto la quantità di vino presente nella botte, funzione del tempo t, con Qv e con C la concentrazione (Qv=V*C). V è costante, ed è il volume della botte, nel nostro caso 100 l. C(t) è la nostra funzione incognita.Facciamo adesso due discorsi separati riguardo alla velocità di variazione del volume del vino nella botte. Chiamiamo R tale velocità; non essendo costante la concentrazione C(t) , possiamo per ora parlare solo di velocità media:

siano ancora t1,t2 due istanti separati da \dpi{120} \Delta t

\dpi{120} \dpi{120} \dpi{120} R_{m}=\frac{\Delta Q_{v}}{\Delta t}=V\cdot \frac{\Delta C}{\Delta t} questa è  sempre una velocità media, che dipenderà dall'intervallo scelto t1,t2.  Per trovare la velocità istantanea dobbiamo sempre fare un passaggio al limite:

  1. \dpi{120} \dpi{120} \dpi{120} R=V\cdot \lim_{\Delta t\rightarrow 0}\frac{\Delta C}{\Delta t}=V\cdot \frac{dC}{dt}. Questo è il legame fra R  e la derivata della nostra funzione C(t). Notare che l'unità di misura di R è  l/min.

D'altro canto (e questo è un altro discorso), la botte è piena e quindi il flusso F=5 l/min diventa tutto di uscita. di miscela. F è già una velocità di variazione volumetrica. La sua velocità è costante, ed è uguale a 5 litri al minuto; ma allora quanto vino esce nell'unità di tempo, cioè qual'è la rapidità di variazione istantanea? Basta moltiplicare F per la concentrazione in quell'istante:

2) R=-F* C(t). Il segno meno sta ad indicare che la variazione è negativa. Notare che l'unità di misura di R è ancora l/min.

Se adesso confrontiamo la 1) con la 2) otteniamo l'equazione differenziale:

\dpi{120} V\cdot \frac{dC}{dt}=-F\cdot C(t)

\dpi{120} \frac{dC}{dt}=-\frac{F}{V}\cdot C(t)

che ha come soluzione generica:

\dpi{120} C(t)=e^{d-\frac{F}{V}\cdot t}=e^{d}\cdot e^{\frac{F}{V}\cdot t} dove d è una costante da ricavarsi con le condizioni iniziali.

infatti \dpi{120} \frac{d}{dt }( e^{d-\frac{F}{V}\cdot t})=\frac{d}{dt}(d-\frac{F}{V})\cdot e^{d-\frac{F}{V}}=-\frac{F}{V}\cdot e^{d-\frac{F}{V}} essendo nulla la derivata d i d che è una costante,

si trova ancora che \dpi{120} C(0)=e^{d}=1/2

\dpi{120} \dpi{120} C(t)=\frac{1}{2} e^{-\frac{F}{V}\cdot t}

N.B. Ho classificato questo problema nella categoria Matematica. Tutti sanno che i rubinetti buttano fuori litri di liquido al secondo. Concentrazione di un una miscela di liquido a parte, non serve alcun concetto di fisica per risolverlo. Almeno io lo vedo come un problema puramente matematico.

 

 

Articoli correlati

4 commenti

  1. Maurizio Bernardi
    23/08/2018 at 21:22

    Una soluzione molto compatta si può ottenere rappresentando la dinamica del  sistema con  una semplice equazione differenziale lineare di primo ordine.

    Indichiamo con y(t) la quantità di vino presente nell'istante t.

    in un intervallo di tempo [t, t + ∆t], la quantità di vino che esce dalla botte è data da:

    \frac{y(t)}{100}5 \Delta t , poiché  \frac{y(t)}{100} è la quantità di vino per litro nell’istante t.

    Abbiamo quindi y(t + ∆t) − y(t) ≈ − (y(t) /20) ∆t ⇒       y' (t) = − y(t) /20

    Questa equazione differenziale è a variabili separabili.

    Integrando (tenendo presente che y può assumere solo valori positivi), otteniamo:

    \int \frac{1}{y}dy=\int \frac{-1}{20}dt    da cui

    log(y)=\frac{-1}{20}t + c     ricavo   quindi la y(t)

    y(t) = e^{\frac{-1}{20}t } e^c

    conosciamo la condizione iniziale (t=0)  che corrisponde all'inizio dell'ora, quando la concentrazione del vino y(0) è  0,5.  Questo valore costituisce il coefficiente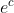   e^c

    Dopo 1 ora , ossia 60', troveremo   y(60) =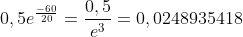0,5 e^\frac{-60}{20} = \frac{0,5}{e^3} = 0,0248935418

     

  2. Umberto
    24/08/2018 at 08:29

    Questo è proprio quello che volevo Maurizio; la soluzione tramite equazione differenziale.

    Chiaramente questa soluzione è corretta, ed è anche la più "canonica".

    Sarò sincero:Didatticamente non sono riuscito a giustificare bene al lettore il passaggio fra le differenze finite e l'equazione differenziale vera e propria, Quindi non ho citato questa soluzione.

    Tu scrivi:

    in un intervallo di tempo [t, t + ∆t], la quantità di vino che esce dalla botte è data da:

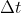    \frac{y(t)}{100}5 \Delta t , poiché  \frac{y(t)}{100} è la quantità di vino per litro nell ’istante t.

    Ma delta  \Delta t è un intervallo finito, y(t) non è costante in tale intervallo, perchè varia di continuo. Qui dovremmo ragionare su dei valori medi.   Poi prosegui:

    Abbiamo quindi y(t + ∆t) − y(t) ≈ − (y(t) /20) ∆t ⇒       y' (t) = − y(t) /20

    Questa equazione differenziale...

    Quello che non si riesce a giustificare bene è quest'ultimo passaggio. NB che nessuno lo fa.  Ci vorrebbe un passaggio al limite per ottenere una dimostrazione rigorosa.

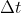    ma pur essendo sicuri che  \frac{y(t+\Delta t)-y(t))}{\Delta t} tenda alla derivata y' per \Delta t -->0, che possiamo dire del valore y(?) a destra. Tende a y(t)? Siamo sicuri che è compreso fra t+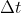\Delta t e t? Questo volevo che qualcuno riuscisse a spiegare bene ai lettori. Spero di essermi spiegato bene.

  3. maurizio bernardi
    25/08/2018 at 00:14

    Si potrebbe partire  dalla struttura dello sviluppo in serie di potenze di Taylor della funzione , ossia la sua ricostruzione nell'intorno di un punto (derivabile indefinitamente) con un polinomio i cui termini sono i valori delle potenze per i coefficienti calcolati nel punto, in funzione delle rispettive derivate. Limitando la sequenza di termini  del polinomio ad  n , abbiamo in ogni caso un Resto Rn.

    Troncando il polinomio alla derivata prima e assumendo il resto R1 trascurabile, si arriva ad una relazione tra derivata prima e funzione che corrisponde nel nostro esempio alla scrittura  y(t + ∆t) − y(t) ≈ − (y(t) /20) ∆t     (si noti il simbolo  ≈  che non corrisponde evidentemente ad =  ma  sottolinea la presenza di una approssimazione).

    Il  valore di y a destra è in ogni caso, per come la relazione è costruita, il valore della funzione in corrispondenza ad un  ∆t tendente a zero, ossia il medesimo y(t) che abbiamo a sinistra.

    Questo dovrebbe rassicurarci sulla legittimità del ragionamento.

     

     

     

  4. Umberto
    25/08/2018 at 08:51

    capisco il tuo ragionamento Maurizio. Cercavo però qualcosa di più semplice. Comunque tu hai fatto un ragionamento non banale che pensa, facevano anche Newton e Leibniz. Loro escludevano i termini piccoli.

    Ma se in fisica è lecito trascurare dei termini piccoli, non lo è in matematica. Era stato Weierstrass a mettere ordine in questi ragionamenti con il concetto di limite. Comunque visto che abbiamo bene o male trovato un'altra soluzione, devo provvedere ad integrarla e a cercare di spiegarla.

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.