Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Eccoci arrivati al dunque; abbiamo adesso a disposizione i concetti base di Topologia, che potete trovare negli approfondimenti o direttamente in questo tag.  Finora abbiamo visto esempi di spazi topologici "esistenti". Ci preoccupiamo ora  di costruire dei nuovi spazi topologici partendo da spazi noti.

Premessa

Appena più avanti, useremo due proprietà degli insiemi e delle funzioni che si sintetizzano così:

Data una funzione f,suriettiva fra due insiemi f:X--->Y ,valgono le due seguenti proprietà:

a) Se Ui è una famiglia di sottoinsiemi di Y, allora

, ovvero la controimmagine dell'unione degli Ui è l'unione delle controimmagini .

b) se U, V sono due sottoinsiemi di X allora

  ovvero la controimmagine dell'intersezione è l'intersezione delle controimmagini.

Vorrei lasciare la facile verifica di queste proprietà al lettore; basta applicare la definizione di controimmagine di un sottoinsieme.

Spazi quoziente

Supponiamo di avere uno spazio  topologico X, un insieme Y, e una qualsiasi funzione f , che però deve essere suriettiva, di X-->Y. Ebbene, abbiamo già creato un nuovo spazio topologico: Y. Per farlo , dobbiamo però definire la topologia su Y, ovvero dare un metodo per definire gli aperti. Chiamiamo U un qualsiasi sottoinsieme di Y. Sappiamo che f è suriettiva, quindi  è un certo sottoinsieme di X, diverso da vuoto. Diciamo che U è un aperto di Y se   è aperto in X.

Con questa definizione Y diventa una topologia. Ricordiamo gli assiomi che devono soddisfare gli aperti per formare una topologia t:

1. l’insieme vuoto e X appartengono a t;
2. l’unione di una qualunque famiglia di elementi di t appartiene ancora a t;
3. l’intersezione di un numero finito di elementi di t appartiene ancora a t.

a: questo è vero perchè ,  . Quindi e Y appartengono a t.

Consideriamo adesso l'unione di una famiglia di Ui aperti; le controimmagini di questi insiemi sono degli aperti in X.

Ma: ; ma essendo  aperti, anche la loro unione in X è un aperto, quindi l'unione degli Ui è un aperto. Quindi vale  b)

Consideriamo adesso l'intersezione di due aperti U,V in Y;  essendo  che è l'intersezione di due aperti in X e che quindi è un aperto. Quindi vale c) e  Y è uno spazio topologico.

Ricordate la definizione di continuità in Topologia?

"Una funzione f: X-->Y fra  due spazi topologici è  continua  se per ogni aperto A di Y,   è un aperto di X."

Ma allora con la topologia definita dalla funzione f,  f diventa automaticamente continua.

Quindi dato uno spazio topologico X, per costruire  un nuovo spazio topologico Y basta dare una funzione f: X--->Y che sia suriettiva. In particolare, possiamo definire una funzione suriettiva partendo da una relazione d'equivalenza.

Consideriamo uno spazio topologico X e una relazione d'equivalenza ; sappiamo che tale relazione crea una partizione di X (X è unione di insiemi disgiunti,detti classi della relazione). Se consideriamo come Y l'insieme delle classi di tale relazione, ovvero  (i due punti significano "tali che"), sappiamo che esiste una funzione naturale che ad ogni x in X associa la sua classe; tale funzione prende anche il nome di proiezione.Y viene anche indicato con   .

Chiamando π tale proiezione, avremo π: X---> Y, π(x)=[x].

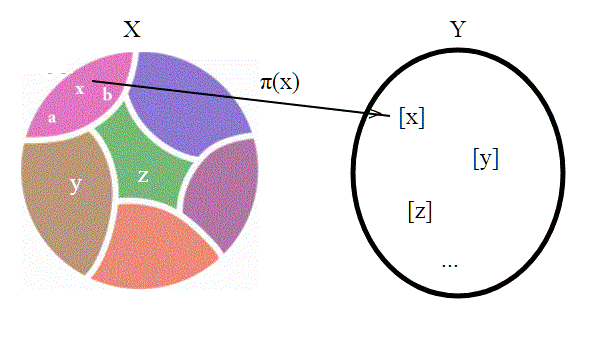
L'applicazione è suriettiva , in quanto ogni elemento ha una classe d'equivalenza (al limite quella rappresentata da se stesso) mentre non è iniettiva (più punti possono finire nello stesso elemento. In tal modo lo spazio quoziente  diventa uno spazio topologico con la topologia relativa alla funzione π.

Il fatto che π  non sia iniettiva, ovvero che come detto sopra possa mandare più punti in uno stesso punto dello spazio topologico Y, fa si che la topologia quoziente prenda il nome di "topologia degli spazi incollati".  In matematica incollare due punti significa far coincidere gli stessi dichiarandoli come equivalenti, e questo si può fare solo con una relazione d'equivalenza. Notare che con la topologia definita da π , lo spazio quoziente di una relazione d'equivalenza non è solo un insieme di punti, ma uno spazio topologico vero e proprio.

Con queste definizioni, riusciremo a fare quello che ha fatto Maurizio con la carta e la colla, ovvero potremmo generare il nastro di Möbius  partendo da un rettangolo e incollandolo matematicamente. Ma andiamo per gradi; cominciamo con un caso semplice.

Generare un cerchio (o meglio una curva chiusa) con un segmento.

Come possiamo nella realtà fisica generare un cerchio partendo da un segmento? Pensiamo ad un filo di ferro.Basta incollarne gli estremi. La stessa procedura la dobbiamo fare matematicamente.

Prendiamo come X=[0,1], che è un intervallo chiuso, sottoinsieme di R.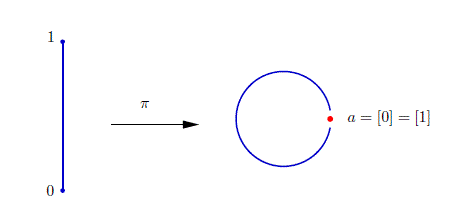

 

consideriamo la relazione d'equivalenza in  X:

 oppure

se t=0 o t=1 i due punti sono equivalenti, quindi la classe di equivalenza possiamo chiamarla indifferentemente [0] = [1]=a

se invece i punti sono interni al segmento aperto (0,1) la relazione d'equivalenza diventa banale: ogni punto è equivalente solo a se stesso. Quindi la proiezione π manda i punti interni al segmento (0,1) in se stessi, mentre manda sia 0 che 1 in a.  Per ora, per quanto detto sopra, siamo solo sicuri che l'insieme quoziente è uno spazio topologico.

Intuitivamente si capisce che è proprio come se piegassimo  il nostro filo incollandolo in a, ottenendo una curva chiusa.

Non possiamo ancora dirlo; dovremmo dimostrare che lo spazio topologico ottenuto è omeomorfo ad un cerchio. E infatti è proprio così, ma ancora non abbiamo gli strumenti per dimostrarlo.

La prossima volta  costruiremo spazi più complessi, fra cui il nastro do Mobius. Ma il procedimento sarà sempre questo.