Questo articolo fa parte della serie "Dante - Riemann - Einstein: Dio e il Big Bang" che è stata inserita nelle sezioni d'archivio "Cosmologia" e "Arte, letteratura e storia della scienza"

 

In questa seconda parte, cercheremo di utilizzare lo stile di Flatlandia per comprendere se è possibile farsi un'idea di come apparirebbe una 3-sfera (appartenente a un 4-spazio) nel nostro 3-spazio. Faremo uso di analogie tra i vari spazi, ma il risultato finale non sarà del tutto soddisfacente. I nostri amici bacherozzi, per quanto arguti ed intelligenti, saranno messi a dura prova!

Lo scopo di questa serie di articoli è quello di arrivare ad avere un'idea meno vaga possibile della 3-sfera. Cercare di rappresentarla compiutamente è lavoro impossibile a meno di non trattarla secondo connessioni più o meno complicate con la topologia di Umberto e con i tori di Arturo.  Noi cerchiamo invece di andare al sodo in fretta, dato che ci vuole abbastanza poco per infilarci  con corpo e mente nell'Universo dantesco.

Ciò non toglie che ci si possa divertire un poco con lo stile di Flatlandia e con le proiezioni, ricordando che noi abbiamo la fortuna di vivere in uno spazio a tre dimensioni e di saperlo rappresentare su un foglio a due dimensioni. Cerchiamo di estrarre le migliori analogie per immaginarci il passo decisivo verso una 3-sfera che è purtroppo immersa in un 4-spazio, luogo per noi inarrivabile. Proveremo, infine, a entrare direttamente sulla 3-sfera, sfruttando la capacità già acquisita di saperci muovere su una 2-sfera. In qualche modo cercheremo di imitare, nel nostro piccolo e molto parzialmente, il fantastico lavoro di Riemann.

Seguiamo lo stile di Flatlandia, cercando più analogie possibili saltando da uno spazio a un altro e iniziando a descrivere come vedrebbe una sfera a 1 dimensione un abitante di uno spazio a 1 dimensione.

Il bacherozzo è quello che avevamo chiamato 1 la volta scorsa e che non ha dimensioni se non la lunghezza, misurata su una retta. Per lui sappiamo che ciò che riesce a descrivere perfettamente è la 0-sfera, rappresentata da due punti. Il che ci fa capire che più di questo non riesce a “vedere”. In realtà, però, noi facciamo muovere la 1-sfera secondo uno dei suoi assi, per esempio l’asse y in Fig. 6, a sinistra, e vediamo come cambia la visione della 1-sfera da parte di B. Attenzione! Per potere disegnare una 1-sfera siamo costretti a inserirla in un 2-spazio, ossia su un piano che ha gli assi x e y.

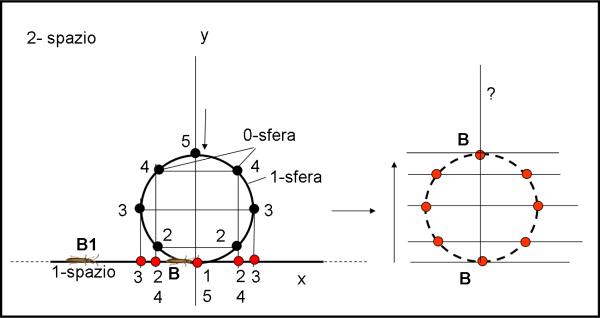
In realtà, non abbiamo nessun bisogno di far muovere veramente la sfera. Ciò che otterremmo, alla fine, non sarebbe altro che la proiezione di tutti i suoi punti sull'1-spazio del bacherozzo.

Consideriamo lo spazio a una dimensione del bacherozzo B e proiettiamo su di lui i vari punti della 1-sfera, che altri non sono che i due punti che caratterizzano la 0-sfera dell'1-spazio. In poche parole, le coppie di punti neri corrispondenti alle intersezioni dell 1-sfera con le parallele all'asse delle x (parallelo all'1 spazio del bacherozzo) vengono proiettati sui punti rossi nell'effettivo 1-spazio di B. Abbiamo posto per semplicità il bacherozzo al centro, lungo l'asse y. Se fosse stato esterno (B1), ossia più lontano, avrebbe sempre visto apparire un solo punto (più o meno vicino a lui) che avrebbe nascosto la vista dell'altro corrispondente alla coppia della 0-sfera.

Il bacherozzo B vede apparire per primo il punto 1, da solo, poi le coppie 2 e 3, sempre più lontane. A questo punto i due punti si avvicinerebbero di nuovo (4) per poi diventare nuovamente uno solo (5) e, infine, sparire.

Nel caso di B, se il bacherozzo fosse Einstein  probabilmente arriverebbe a concepire una 1-sfera pur vivendo in  1-spazio, come mostrato nella parte destra della figura. Non  dimentichiamoci, infatti, che  anche lui si è immaginato e ha descritto una 3-sfera (aiutato dalle varietà di Riemann), pur vivendo in uno spazio a 3 dimensioni… Per Einstein la quarta dimensione è il tempo, per il bacherozzo una qualche dimensione immaginaria.

Fino a qui, non abbiamo fatto altro che seguire in qualche modo la "semplicità" di Flatlandia. Purtroppo le possibili situazioni sono ben più complesse … e ci fanno capire che la 1-sfera può “proiettarsi” in vari modi lungo l’1-spazio euclideo del nostro bacherozzo che resterà molto confuso. La sua intelligenza sarà messa a dura prova…

Ricordiamo ancora che fare muovere la 1-sfera lungo l’asse y verso il basso è del tutto equivalente a far muovere l’asse x (l’1-spazio del bacherozzo) verso l’alto o, ancora più semplicemente, proiettare i punti della 1-sfera sull'1-spazio del bacherozzo.

Disegniamo la Fig. 7, dove questa volta incliniamo di un certo angolo φ  la direzione di movimento della nostra 1-sfera.

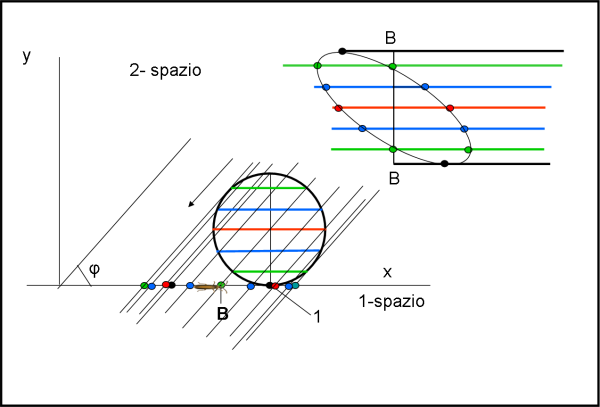
Per semplicità inseriamo il bacherozzo sull'asse x proprio dove la direzione del centro della 1-sfera incontra l'asse x (l'1-spazio del bacherozzo). Come abbiamo già imparato nel caso precedente, basta proiettare una serie di 0-sfere sull'asse del bacherozzo per vedere in quali punti la 1-sfera attraversa l'asse x. Abbiamo usato colori diversi per non fare confusione (gli stessi colori prima e dopo che è passata mezza 1-sfera). Le cose sono decisamente più complicate e il bacherozzo Einstein si troverebbe sicuramente in grande confusione. Al limite, potrebbe anche fare come nel caso precedente e disegnare le 0-sfere viste durante il transito distanziandole lungo un certo asse immaginario (che noi sappiamo essere l'asse y). Il risultato sarebbe ciò che vediamo nella parte destra della figura... una bella ellisse che ben poco ha a che fare con una 1-sfera.

Senza usare formule, è chiaro che più l'angolo φ si avvicina a 0  e più l'ellisse si allunga, mentre per φ = 90° si torna nel caso di Fig. 6. Notiamo che per φ = 0, il bacherozzo vedrebbe sempre almeno un punto, prima a destra e poi a sinistra. La distanza tra i due valori estremi diventerebbe infinita. Ah... queste proiezioni... che problema  per il nostro bacherozzo! Tuttavia, teniamo presente che sono l'unica informazione che il bacherozzo può avere su una 1- sfera. Solo l'insieme di tutte loro possono avvicinare il bacherozzo dell'1-spazio a ciò che si può vedere solo nel 2-spazio.

Potremmo anche fare casi ancora più complicati, con rotazioni varie e molto altro ancora. Il bacherozzo sarebbe sempre  più confuso...

Il passaggio alla 2-sfera e al bacherozzo piatto, ma a due dimensioni che vive su un 2-spazio, è abbastanza semplice e intuitiva. E Flatlandia la descrive molto bene... Tuttavia per eseguire il disegno siamo costretti a immergere la 2-sfera in un 3-spazio (come prima avevamo immerso la 1-sfera in un 2-spazio). Le nostre figure devono perciò contenere anche l'asse z... Immaginiamo che la situazione sia quella di Fig. 8 , in alto.

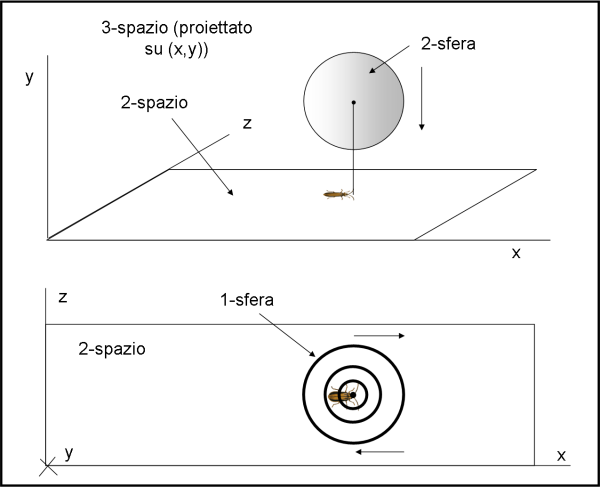
A noi interessa descrivere cosa si vede mentre la sfera scende lungo y sul  2-spazio (x,z).  Mentre prima eravamo vincolati al piano del foglio (2-spazio) e potevamo solo utilizzare 1-spazi che stavano su quel piano, ora vi è la possibilità di usare come mondi del bacherozzo tutti i piani che vogliamo, orientati come si vuole rispetto ai tre assi (x,y,z).

La cosa migliore, forse, sarebbe vedere il tutto dall'alto, ossia con l'asse y rivolto verso di noi (parte bassa della figura) . Bene, il nostro bacherozzo vedrebbe un punto e poi delle 1-sfere (circonferenze) sempre più grandi fino a un certo valore massimo. Dopo di che inizierebbero a restringersi fino a ridursi a un punto e scomparire. Abbiamo ovviamente usato la proiezione della 2- sfera lungo l'asse delle y.

E se la proiezione non avvenisse lungo la y? Ammettiamo che l'asse del cilindro di proiezione formi un certo angolo con il piano (x,z). La situazione è del tutto analoga a quella vista in Fig.7. Si aggiunge, però, il fatto che ora non si tratta solo di segmenti, ma di circonferenze di raggio e centro variabili.

La Fig. 9 cerca di sintetizzare il tutto guardando la 2-sfera azzurra nel piano (x,y), con l'asse z diretto verso di noi, per determinare i punti di contatto sul piano (x,z) delle proiezioni delle 1-sfere  che le appartengono (parte alta). In basso abbiamo invece proprio ciò che si vede nel piano del bacherozzo (x,z), con l'asse y diretto verso di noi.

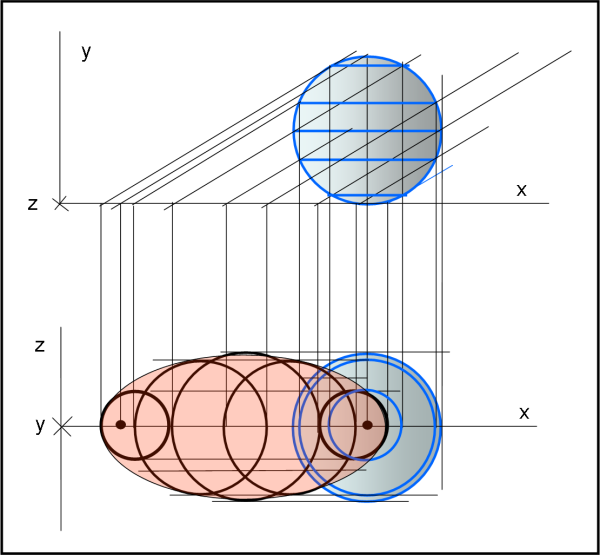
Un piccolo gioco geometrico proiettivo... niente di più. La figura in basso ci mostra, con le circonferenze (1-sfere) proiettate in nero, qual è la situazione sul piano del bacherozzo. Si vede subito che l'insieme delle 1-sfere è inviluppato da una 1-ellisse (color rosa). Se il bacherozzo fosse sempre Einstein potrebbe  disegnare le 1-sfere viste durante il transito distanziandole lungo un certo asse immaginario (che noi sappiamo essere l'asse y). Il risultato è facilmente intuibile, senza nessun bisogno di fare la figura corrispondente: sarebbe un ellissoide nel 3-spazio, cosa ben diversa da una 2-sfera.

In generale, essendo immerso nel 3-spazio sarebbe visibile sotto svariati punti di vista da noi fortunati bacherozzi a tre dimensioni, che probabilmente prenderemmo in giro la faticosa ricostruzione eseguita dal bacherozzo Einstein costretto a vivere nel 2-spazio e immaginarsi un 3-spazio. Ciò che è una 2-sfera sarebbe immaginata come una figura ben diversa dalla realtà dei fatti.

Anche la classica figura della 2-sfera tagliata a fette di Fig. 10 sembra solo apparentemente migliorare la situazione.

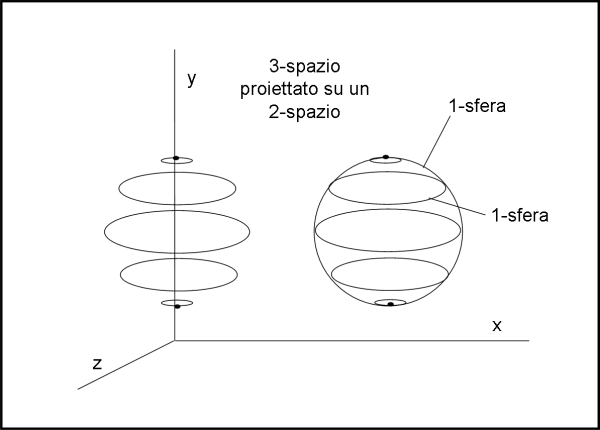
Noi, bacherozzi del 3-spazio vedremmo una bella 2-sfera e ogni sua sezione sarebbe una 1-sfera. Eh no, cari amici! Le sue sezioni non sarebbero assolutamente delle 1-sfere, ma delle 1-ellissi, come si vede chiaramente.  La nostra abitudine a proiettare un 3-spazio sul piano del foglio (2-spazio) ci porta a identificare immediatamente un'ellisse come la proiezione di una circonferenza.  Ci possiamo permettere tutto ciò perché sappiamo com'è fatta una 2-sfera. Insomma, anche questa figura che sembra molto più istruttiva, è pur sempre un proiezione sul piano (x,y)(2-spazio). Vedremmo l'inviluppo delle varie sezioni come una circonferenza (una 1-sfera) e vedremmo le sezioni come strane figure (1-ellissi). Per risalire alla 2-sfera ci vorrebbe comunque un'opera di costruzione mentale.

Sì, ma non ridiamo troppo del povero bacherozzo a 2 dimensioni... perché adesso tocca a noi...

Purtroppo noi non conosciamo affatto la forma di una 3-sfera immersa in un 4-spazio e, di conseguenza, quello che pensiamo di vedere come sua proiezione nel 3-spazio è del tutto parziale. Cosa vedremmo infatti, lavorando solo sull'analogia? Beh... se una 2-sfera tagliata a fette ci regala tante 1-sfera, una 3-sfera tagliata a fette dovrebbe darci tante 2-sfere (Fig. 11).

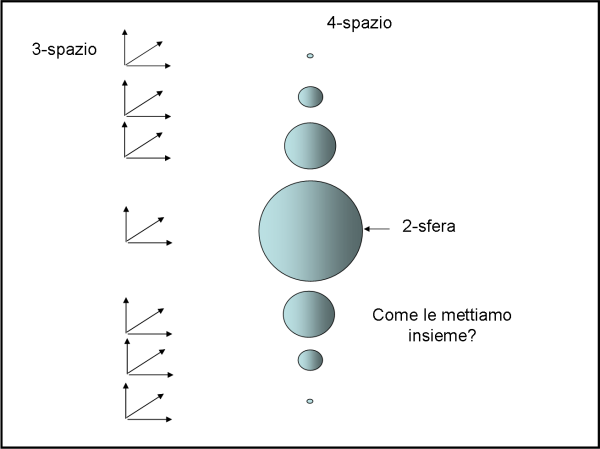
OK... andiamo avanti con l'analogia. Cosa facciamo delle tante fette 1-sfera? le mettiamo una sopra l'altra e costruiamo una bellissima 2-sfera. Bene, proviamo allora a mettere insieme, una sull'altra le tante 2-sfere... No, non sapremmo assolutamente come fare. Potremmo solo pensare che la 3-sfera sia formata da tante 2-sfere che si susseguono (o che si proiettano) lungo un qualche asse del tutto invisibile. Esse, in realtà compaiono da nulla, una dopo l'altra, ma non siamo in grado di ricostruire la figura nel 4-spazio. Dobbiamo perciò accontentarci di sapere che una possibile proiezione nel 3-spazio può dare luogo a quella serie di tante sfere (dalla più piccola alla più grande), per poi diminuire nuovamente. Non conosceremmo, però, altre possibili proiezioni... Un risultato non del tutto soddisfacente.

Siamo davanti a un bivio. O entrare prepotentemente nella matematica e nella topologia più complessa, ottenendo, però, figure sempre e  comunque molto parziali e praticamente incomprensibili, oppure deciderci di andare a vivere proprio sulla 3-sfera, sapendo di dovere abbandonare lo spazio euclideo. Per ottenere qualche informazione in più, il nostro bacherozzo deve cambiare modo di pensare e noi con lui... Non ci resta perciò che seguire Riemann e agire con molta calma e attenzione, muovendosi su uno spazio curvo, iniziando a considerarlo del tutto normale in un piccolo intervallo intorno a noi.