Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

Un piccolo esercizio di meccanica classica per i nostri amici  astronauti sempre in giro per conoscere le meraviglie dell'Universo. Un problema, tuttavia, che viene normalmente affrontato anche nella realtà.

I nostri amici astronauti stanno navigando all’interno di un sistema planetario praticamente sconosciuto. Vedono diversi pianeti molto invitanti, ma, prima di scendere su di loro, vorrebbero sapere le condizioni che troverebbero una volta giunti al suolo. In particolare quanto vale l’accelerazione di gravità, da cui dipende il loro peso.

Fortunatamente, il più attraente, ha anche un satellite in orbita perfettamente circolare. L’unica cosa che conoscono i nostri amici è la distanza tra loro e il pianeta. Sono, comunque muniti di una strumentazione minima, tale da permettergli di misurare angoli anche molto piccoli.

Come devono sistemare la loro astronave (senza avvicinarsi troppo per non consumare carburante) e quali calcoli devono fare per trovare rapidamente l’accelerazione di gravità del pianeta ? Tralasciamo la figura, altrimenti la risposta diventa veramente ridicola…

Basta applicare due volte la legge di gravitazione universale che conoscono molto bene…

Senza avvicinarsi troppo (la strumentazione è più che buona per misurare angoli piccoli), i nostri amici sistemano l’astronave in modo da semplificare la visione dell’orbita del satellite. In altre parole, la direzione pianeta-astronave è perpendicolare al piano orbitale del satellite, come mostrato nella Fig. 1. Tutto diventa piuttosto facile. In particolare, misurare l’angolo β sotteso dall’orbita (circolare) di raggio r del satellite (basta misurare l’angolo tra centro del pianeta e satellite) e l’angolo α sotteso dal diametro del pianeta (2R).

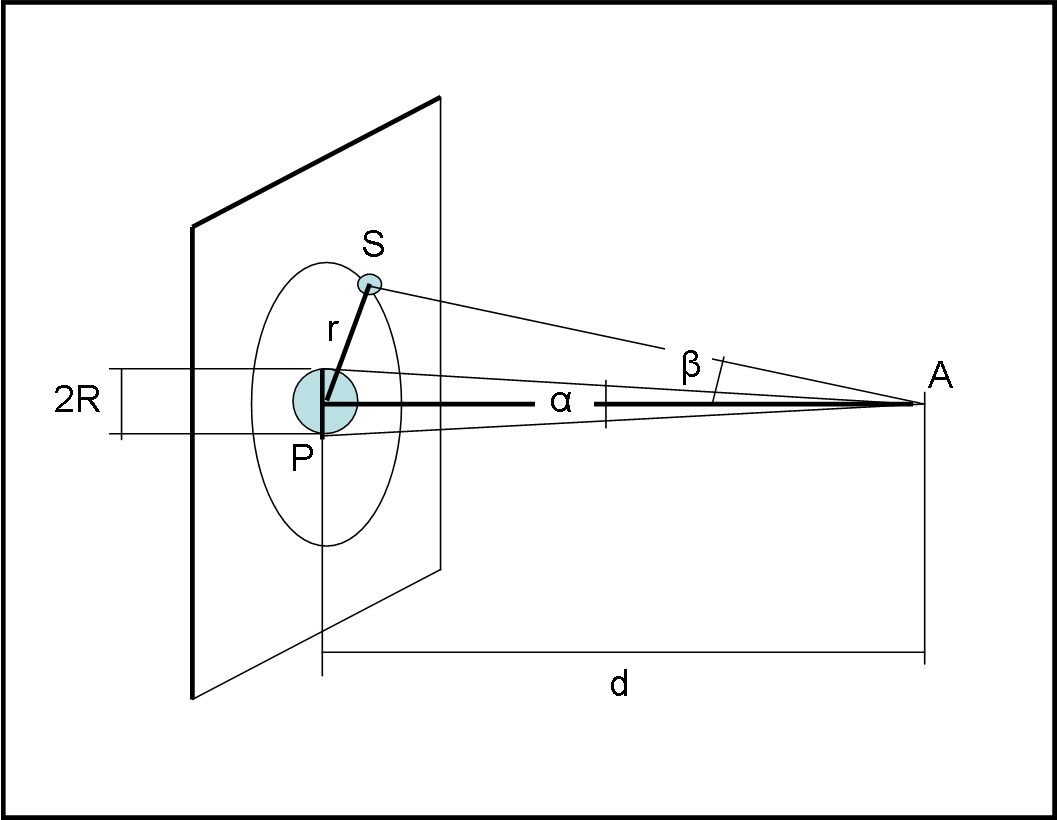
Conoscendo la distanza d (pianeta-astronave) è immediato calcolare il raggio r dell’orbita del satellite e il raggio R del pianeta

R = d tan (α/2)

r = d tan (β)

L’orbita del satellite è ben osservabile e non è difficile dedurre il periodo P in cui viene completata.

Se un satellite di massa m è in orbita attorno a un pianeta di massa M sappiamo benissimo quale legge deve seguire: quella di gravitazione universale. La forza a cui è soggetto il satellite è data da:

F = ma_S = GMm/r²

a_S = GM/r²

l’accelerazione a_s non è altro che l’accelerazione di gravità calcolata alla distanza r. Essa deve pareggiare l’accelerazione centrifuga, per cui:

GM/r² = ω²r       …. (1)

La velocità angolare ω è conosciuta, dato che è conosciuto il periodo P, e vale la ben nota relazione:

ω = 2π/P

Dalla (1) possiamo ricavare GM (costante):

GM = ω²r³              …. (2)

Immaginando soltanto, adesso,  di scendere sul suolo del pianeta. Possiamo dire che anche chi si trova in quella posizione è soggetto alla gravità del pianeta: cambia solo la distanza dal centro, che adesso è R.

Risulta allora:

a_P = GM/R²

a_P = g è proprio l’accelerazione di gravità che vogliamo trovare. Scriviamo allora:

GM = gR²

Ricordando la (2) possiamo uguagliare le due espressioni e ottenere, infine:

g = ω²r³/R²

Un calcolo che si può fare, ovviamente, senza scendere al suolo.

Tutto OK? Bene, adesso possiamo atterrare (o applanetare ?) senza rischiare...